第七十八课 最短路径（Dijkstra）

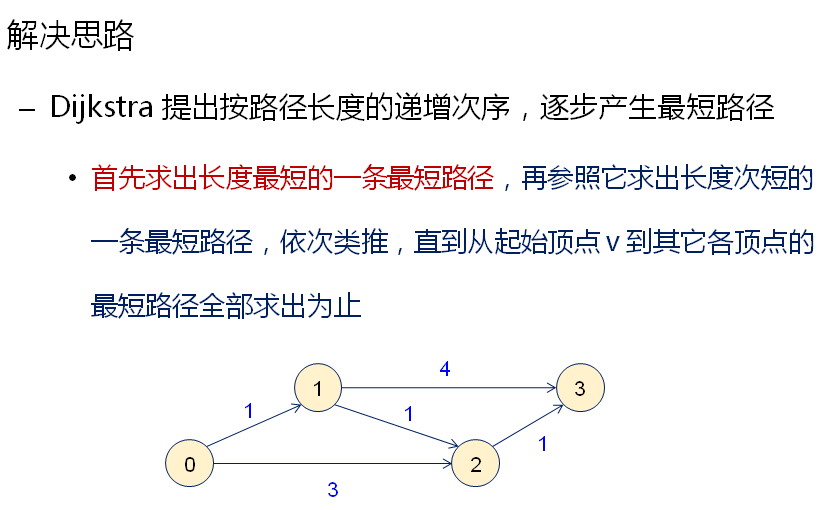
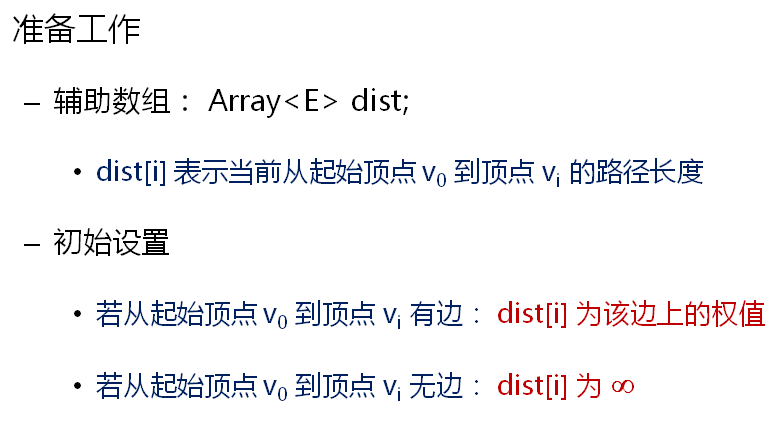
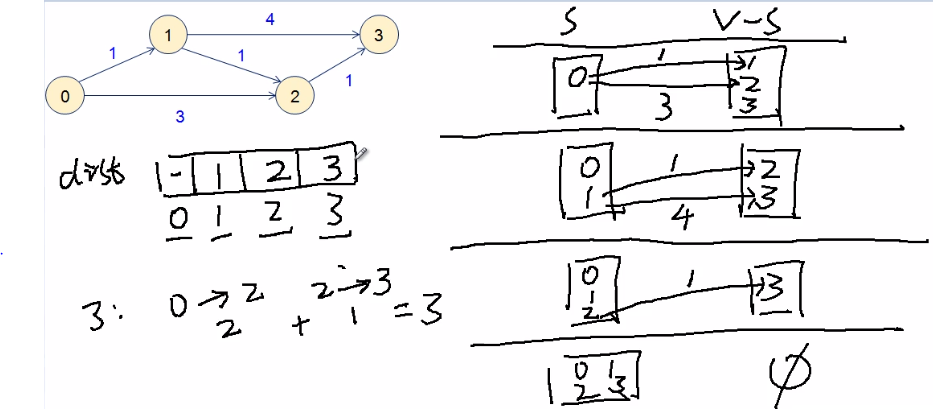
核心思想是从已知的最短路径推算未知的最短路径。

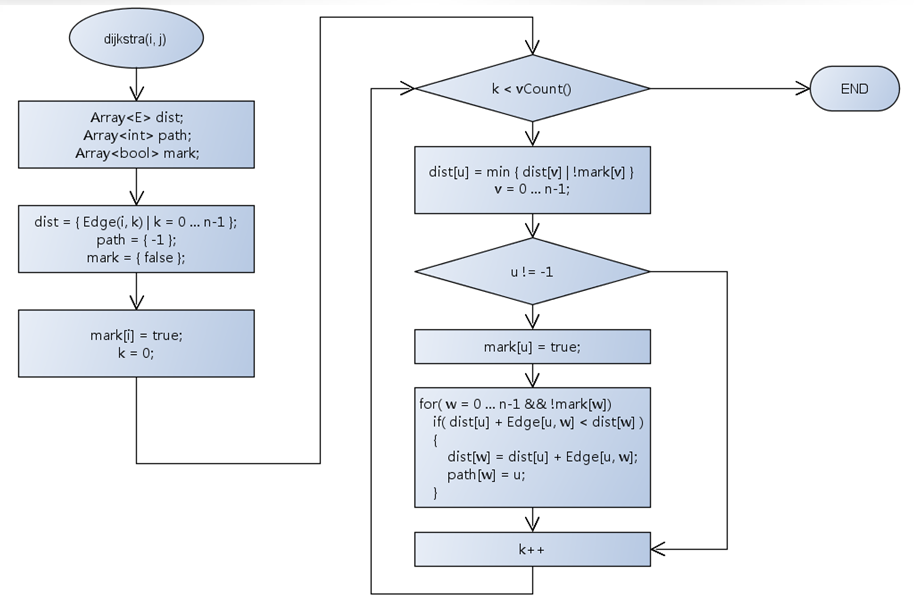
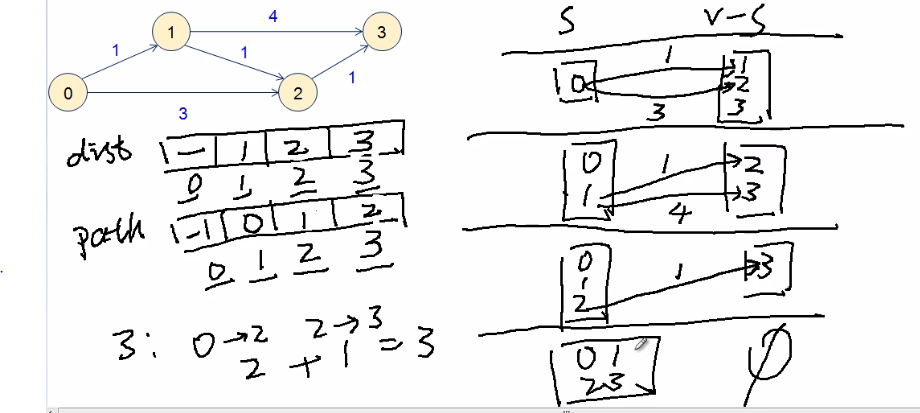
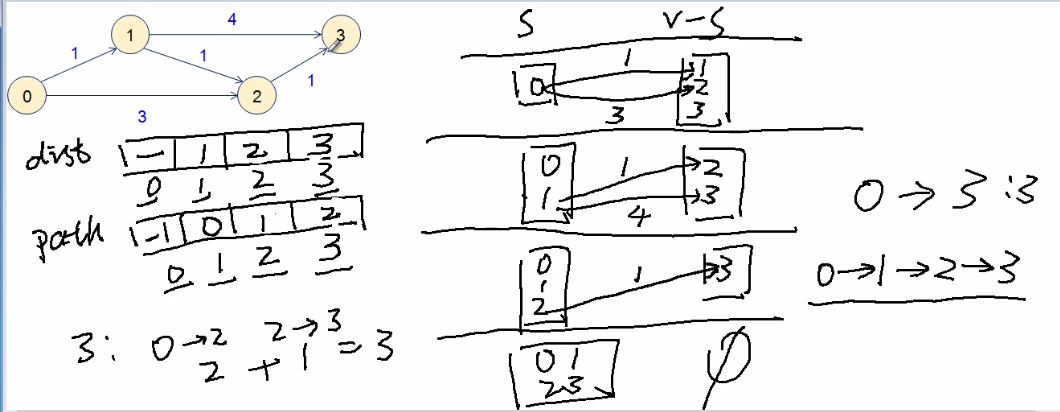
添加程序：

 #ifndef GRAPH_H
 #define GRAPH_H

 #include "Object.h"
 #include "SharedPointer.h"
 #include "Array.h"
 #include "DynamicArray.h"
 #include "LinkQueue.h"
 #include "LinkStack.h"
 #include "Sort.h"

 namespace DTLib
 {

 template < typename E >
 struct Edge : public Object
 {
     int b;
     int e;
     E data;

     Edge(int i=-, int j=-)
     {
         b = i;
         e = j;
     }

     Edge(int i, int j, const E& value)
     {
         b = i;
         e = j;
         data = value;
     }

     bool operator == (const Edge<E>& obj)
     {
         return (b == obj.b) && (e == obj.e);  //在这里不关注权值大小
     }

     bool operator != (const Edge<E>& obj)
     {
         return !(*this == obj);
     }

     bool operator < (const Edge<E>& obj)
     {
         return (data < obj.data);
     }

     bool operator > (const Edge<E>& obj)
     {
         return (data > obj.data);
     }
 };

 template < typename V, typename E >
 class Graph : public Object
 {
 protected:
     template < typename T >
     DynamicArray<T>* toArray(LinkQueue<T>& queue)
     {
         DynamicArray<T>* ret = new DynamicArray<T>(queue.length());

         if( ret != NULL )
         {
             for(int i=; i<ret->length(); i++, queue.remove())
             {
                 ret->set(i, queue.front());
             }
         }
         else
         {
             THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create ret object...");
         }

         return ret;
     }

     SharedPointer< Array<Edge<E> > > getUndirectedEdges()
     {
         DynamicArray<Edge<E>>* ret = NULL;

         if( asUndirected() )
         {
             LinkQueue<Edge<E>> queue;

             for(int i=; i<vCount(); i++)
             {
                 for(int j=i; j<vCount(); j++)
                 {
                     if( isAdjacent(i, j) )
                     {
                         queue.add(Edge<E>(i, j, getEdge(i, j)));
                     }
                 }
             }

             ret = toArray(queue);
         }
         else
         {
             THROW_EXCEPTION(InvalidOperationException, "This function is for undirected graph only...");
         }

         return ret;
     }

     int find(Array<int>& p, int v)
     {
         while( p[v] != -)
         {
             v = p[v];
         }

         return v;
     }
 public:
     virtual V getVertex(int i) = ;
     virtual bool getVertex(int i, V& value) = ;
     virtual bool setVertex(int i, const V& value) = ;
     virtual SharedPointer< Array<int> > getAdjacent(int i) = ;
     virtual bool isAdjacent(int i, int j) = ;
     virtual E getEdge(int i, int j) = ;
     virtual bool getEdge(int i, int j, E& value) = ;
     virtual bool setEdge(int i, int j, const E& value) = ;
     virtual bool removeEdge(int i, int j) = ;
     virtual int vCount() = ;
     virtual int eCount() = ;
     virtual int OD(int i) = ;
     virtual int ID(int i) = ;

     virtual int TD(int i)
     {
         return ID(i) + OD(i);
     }

     bool asUndirected()
     {
         bool ret = true;

         for(int i=; i<vCount(); i++)
         {
             for(int j=; j<vCount(); j++)
             {
                 if( isAdjacent(i, j) )
                 {
                     ret = ret && isAdjacent(j, i) && (getEdge(i, j) == getEdge(j, i));
                 }
             }
         }

         return ret;
     }

     SharedPointer< Array< Edge<E > > > prim(const E& LIMIT, const bool MINIUM = true) //参数为理论上的最大权值
     {
         LinkQueue< Edge<E> > ret;

         if( asUndirected() )
         {
             DynamicArray<int> adjVex(vCount());
             DynamicArray<bool> mark(vCount());
             DynamicArray<E> cost(vCount());
             SharedPointer< Array<int> > aj = NULL;
             bool end = false;
             int v = ;

             for(int i=; i<vCount(); i++)
             {
                 adjVex[i] = -;
                 mark[i] = false;
                 cost[i] = LIMIT;
             }

             mark[v] = true;

             aj = getAdjacent(v);

             for(int j=; j<aj->length(); j++)
             {
                 cost[(*aj)[j]] = getEdge(v, (*aj)[j]);
                 adjVex[(*aj)[j]] = v;
             }

             for(int i=; (i<vCount()) && !end; i++)
             {
                 E m = LIMIT;
                 int k = -;

                 for(int j=; j<vCount(); j++)
                 {
                     if( !mark[j] && (MINIUM ? (cost[j] < m) : (cost[j] > m)))
                     {
                         m = cost[j];
                         k = j;
                     }
                 }

                 end = (k == -);

                 if( !end )
                 {
                     ret.add(Edge<E>(adjVex[k], k, getEdge(adjVex[k], k)));

                     mark[k] = true;

                     aj = getAdjacent(k);

                     for(int j=; j<aj->length(); j++)
                     {
                         if( !mark[(*aj)[j]] && (MINIUM ? (getEdge(k, (*aj)[j]) < cost[(*aj)[j]]) : (getEdge(k, (*aj)[j]) > cost[(*aj)[j]])) )
                         {
                             cost[(*aj)[j]] = getEdge(k, (*aj)[j]);
                             adjVex[(*aj)[j]] = k;
                         }
                     }
                 }
             }
         }
         else
         {
             THROW_EXCEPTION(InvalidOperationException, "Prim operator is for undirected graph only...");
         }

         if( ret.length() != (vCount() - ) )
         {
             THROW_EXCEPTION(InvalidOperationException, "No enough edge for prim operation...");
         }

         return toArray(ret);
     }

     SharedPointer< Array<Edge<E> > > kruskal(const bool MINMUM = true)
     {
         LinkQueue< Edge<E> > ret;

         SharedPointer< Array< Edge<E> > > edges = getUndirectedEdges();

         DynamicArray<int> p(vCount()); //前驱标记数组

         for(int i=; i<p.length(); i++)
         {
             p[i] = -;
         }

         Sort::Shell(*edges, MINMUM);

         for(int i=; (i<edges->length()) && (ret.length() < (vCount() - )); i++)
         {
             int b = find(p, (*edges)[i].b);
             int e = find(p, (*edges)[i].e);

             if( b != e )
             {
                 p[e] = b;

                 ret.add((*edges)[i]);
             }
         }

         if( ret.length() != (vCount() - ) )
         {
             THROW_EXCEPTION(InvalidOperationException, "No enough edges for Kruskal operation...");
         }

         return toArray(ret);
     }

     SharedPointer< Array<int> > BFS(int i)
     {
         DynamicArray<int>* ret = NULL;

         if( ( <= i) && (i < vCount()) )
         {
             LinkQueue<int> q;
             LinkQueue<int> r;
             DynamicArray<bool> visited(vCount());

             for(int i=; i<visited.length(); i++)
             {
                 visited[i] = false;
             }

             q.add(i);

             while( q.length() >  )
             {
                 int v = q.front();

                 q.remove();

                 if( !visited[v] )
                 {
                     SharedPointer< Array<int> > aj = getAdjacent(v);

                     for(int j=; j<aj->length(); j++)
                     {
                         q.add((*aj)[j]);
                     }

                     r.add(v);

                     visited[v] = true;
                 }
             }

             ret = toArray(r);
         }
         else
         {
             THROW_EXCEPTION(InvalidParameterException, "Index i is invalid...");
         }

         return ret;
     }

     SharedPointer< Array<int> > DFS(int i)
     {
         DynamicArray<int>* ret = NULL;

         if( ( <= i) && (i < vCount()) )
         {
             LinkStack<int> s;
             LinkQueue<int> r;
             DynamicArray<bool> visited(vCount());

             for(int j=; j<visited.length(); j++)
             {
                 visited[j] = false;
             }

             s.push(i);

             while( s.size() >  )
             {
                 int v = s.top();

                 s.pop();

                 if( !visited[v] )
                 {
                     SharedPointer< Array<int> > aj = getAdjacent(v);

                     for(int j=aj->length() - ; j>=; j--)
                     {
                         s.push((*aj)[j]);
                     }

                     r.add(v);

                     visited[v] = true;
                 }
             }

             ret = toArray(r);
         }
         else
         {
             THROW_EXCEPTION(InvalidParameterException, "Index i is invalid...");
         }

         return ret;
     }

     SharedPointer<Array<int>> dijkstra(int i, int j, const E& LIMIT)
     {
         LinkQueue<int> ret;

         if( ( <= i) && (i < vCount()) && ( <= j) && (j < vCount()) )
         {
             DynamicArray<E> dist(vCount());
             DynamicArray<int> path(vCount());
             DynamicArray<bool> mark(vCount());

             for(int k=; k<vCount(); k++)
             {
                 mark[k] = false;
                 path[k] = -;

                 dist[k] = isAdjacent(i, k) ? (path[k] = i, getEdge(i, k)) : LIMIT;
             }

             mark[i] = true;

             for(int k=; k<vCount(); k++)
             {
                 E m = LIMIT;
                 int u = -;

                 for(int w=; w<vCount(); w++)
                 {
                     if( !mark[w] && (dist[w] < m) )
                     {
                         m = dist[w];
                         u = w;
                     }
                 }

                 if( u == - )
                 {
                     break;
                 }

                 mark[u] = true;

                 for(int w=; w<vCount(); w++)
                 {
                     if( !mark[w] && isAdjacent(u, w) && (dist[u] + getEdge(u, w) < dist[w]) )
                     {
                         dist[w] = dist[u] + getEdge(u, w);
                         path[w] = u;
                     }
                 }
             }

             LinkStack<int> s;

             s.push(j);

             for(int k=path[j]; k != -; k=path[k])
             {
                 s.push(k);
             }

             while( s.size() >  )
             {
                 ret.add(s.top());

                 s.pop();
             }
         }
         else
         {
             THROW_EXCEPTION(InvalidParameterException, "Index<i, j> is invalid...");
         }

         if( ret.length() <  )
         {
             THROW_EXCEPTION(ArithmeticException, "There is no path grom i to j...");
         }

         return toArray(ret);
     }
 };

 }

 #endif // GRAPH_H

测试程序如下：

 #include <iostream>
 #include "MatrixGraph.h"
 #include "ListGraph.h"

 using namespace std;
 using namespace DTLib;

 template< typename V, typename E >
 Graph<V, E>& GraphEasy()
 {
     static MatrixGraph<, V, E> g;

     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );

     return g;
 }

 template< typename V, typename E >
 Graph<V, E>& GraphComplex()
 {
     static ListGraph<V, E> g();

     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );

     g.setEdge(, , );
     g.setEdge(, , );

     return g;
 }

 int main()
 {
     Graph<int, int>& g = GraphComplex<int, int>();
     SharedPointer< Array<int> > p = g.dijkstra(, , );

     for(int i=; i<p->length(); i++)
     {
         cout << (*p)[i] << " ";
     }

     cout << endl;

     return ;
 }

结果如下：

小结：