Vijos 1360 - 八数码问题 - [A*]

题目链接：https://vijos.org/p/1360

优先队列BFS：

这个八数码问题本身其实是之前人工智能实验课的作业……

首先，如果不带估价函数，直接用优先队列BFS，肯定也是能得到正确结果的，至于用时怎么样，可以看评测结果……

代码：

#include<bits/stdc++.h>
using namespace std;
int dx[]={,,,-};
int dy[]={,-,,};
string ed="";
struct Node
{
    int dist;
    int x,y;
    string mp;

    #define X(idx) (idx/3)
    #define Y(idx) (idx%3)
    char& val(int i,int j){return mp[i*+j];}

    void Zero()
    {
        for(int i=;i<;i++)
        {
            if(mp[i]!='') continue;
            x=X(i), y=Y(i); break;
        }
    }

    bool operator<(const Node& o)const{return dist>o.dist;}
}st;
map<string,bool> vis;
priority_queue<Node> Q;
int main()
{
    cin>>st.mp;
    st.dist=;
    st.Zero();

    vis.clear();
    Q.push(st), vis[st.mp]=;
    while(Q.size())
    {
        Node now=Q.top(); Q.pop();
        if(now.mp==ed)
        {
            cout<<now.dist<<endl;
            break;
        }
        for(int k=;k<;k++)
        {
            Node nxt=now;
            nxt.x+=dx[k], nxt.y+=dy[k], nxt.dist++;
            if(nxt.x< || nxt.x> || nxt.y< || nxt.y>) continue;
            swap(nxt.val(now.x,now.y),nxt.val(nxt.x,nxt.y));
            if(!vis[nxt.mp]) Q.push(nxt), vis[nxt.mp]=;
        }
    }
}

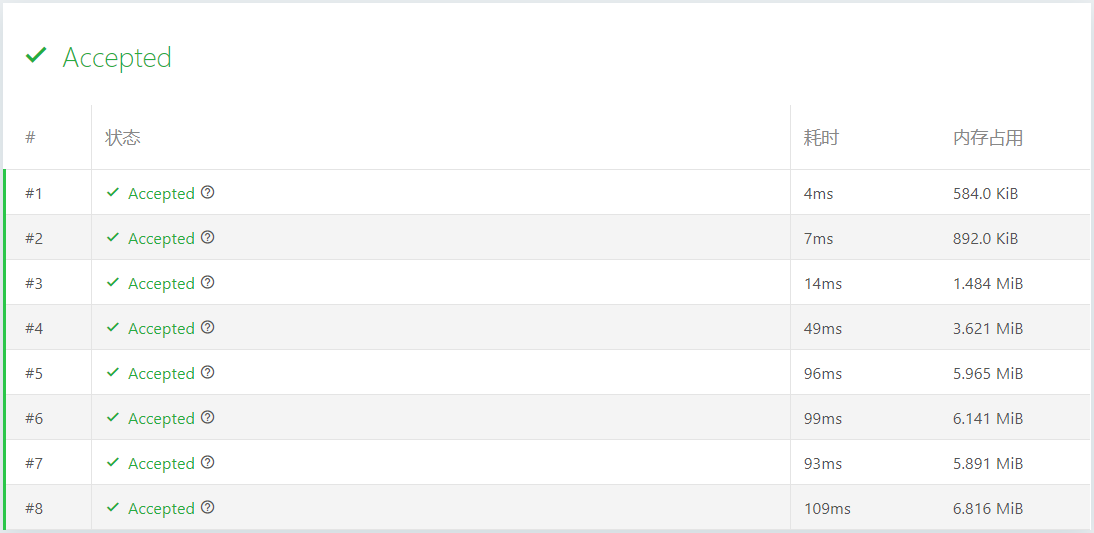
评测结果：

Astar算法：

然后，我们知道，优先队列BFS里的优先队列，是一个维护当前代价的二叉堆，

我们接下来增加Astar算法的估价函数 $eval(x)$，考虑到要这个估价函数，是要不大于从当前状态到目标状态的实际代价的，

因此我考虑将其设定成：将当前状态下的九宫格看做一个长度为 $9$ 的字符串 $s$，目标状态也可以看做一个字符串 $t = "123804765"$，统计这两个字符串使得 $s_i \neq t_i$ 的 $i$ 的个数，记为 $e$，再取 $eval(x) = \lfloor \frac{e}{2} \rfloor$ 即可。

这也是很好理解的，因为不可能用更少的步数使得当前状态变为目标状态了。

AC代码：

#include<bits/stdc++.h>
using namespace std;
int dx[]={,,,-};
int dy[]={,-,,};
string ed="";
struct Node
{
    int dist,eval;
    int x,y;
    string mp;

    #define X(idx) (idx/3)
    #define Y(idx) (idx%3)
    char& val(int i,int j){return mp[i*+j];}

    void Zero()
    {
        for(int i=;i<;i++)
        {
            if(mp[i]!='') continue;
            x=X(i), y=Y(i); break;
        }
    }

    void Eval()
    {
        eval=;
        for(int i=;i<;i++) eval+=(mp[i]!=ed[i]);
        eval/=;
    }

    bool operator<(const Node& o)const
    {
        return dist+eval>o.dist+o.eval;
    }
}st;
map<string,bool> vis;
priority_queue<Node> Q;
int main()
{
    cin>>st.mp;
    st.dist=;
    st.Zero();
    st.Eval();

    vis.clear();
    Q.push(st), vis[st.mp]=;
    while(Q.size())
    {
        Node now=Q.top(); Q.pop();
        if(now.mp==ed)
        {
            cout<<now.dist<<endl;
            break;
        }
        for(int k=;k<;k++)
        {
            Node nxt=now;
            nxt.x+=dx[k], nxt.y+=dy[k], nxt.dist++;
            if(nxt.x< || nxt.x> || nxt.y< || nxt.y>) continue;
            swap(nxt.val(now.x,now.y),nxt.val(nxt.x,nxt.y));
            if(!vis[nxt.mp])
            {
                nxt.Eval();
                Q.push(nxt), vis[nxt.mp]=;
            }
        }
    }
}

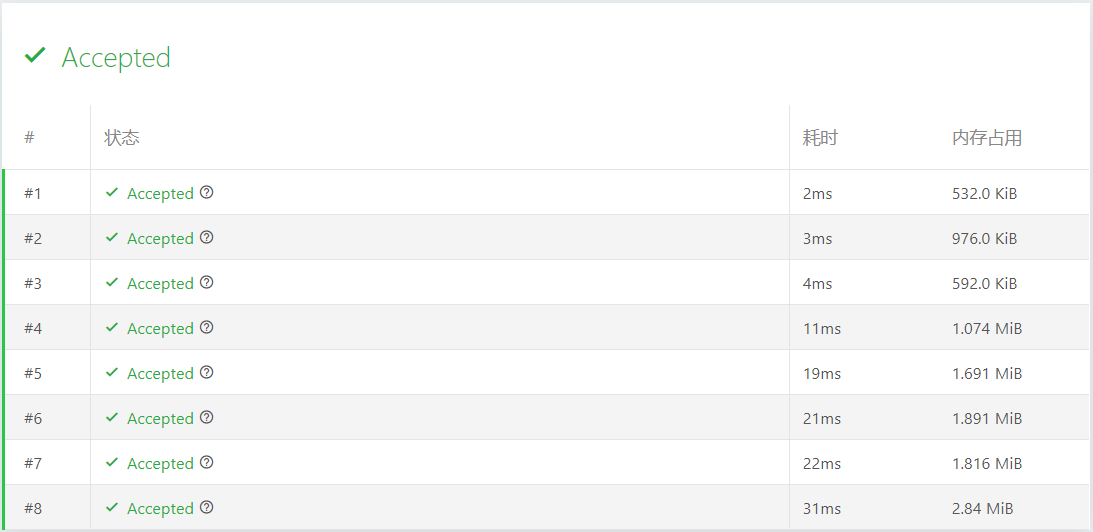
评测结果：

总结：

比较普通的优先队列维护下的BFS，和加了估价算法的Astar算法，可以明显看到时间和空间的使用都明显降低了。

（鉴于有可能会有同样在做这个实验的同学搜索到本文，我还是要声明一下：上面的两个代码都是我亲手敲的，没有看网上任何别的博客，想要拿去借鉴的同学，建议看懂了之后根据自己的思路做一些修改乃至优化……直接抄袭这样的事情最好还是不要做……）