MT【9】绝对值二次函数
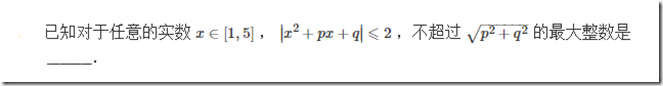
解答:

评:容易用绝对值不等式证明当$x\in[1,5]$时$|x^2+px+q|\ge2$
MT【9】绝对值二次函数的更多相关文章
- MT【329】二次函数系数的最大最小
已知二次函数$f(x)=ax^2+bx+c$有零点,且$a+b+c=1$ 若$t=\min\{a,b,c\}$求$t$的最大值. 分析:由$a,c$的对称性,不妨$c\ge a$即$2a+b\le1$ ...
- MT【219】构造二次函数
(2012北大保送)已知$f(x)$是二次函数,且$a,f(a),f(f(a)),f(f(f(a)))$是正项等比数列;求证:$f(a)=a$ 构造二次函数$f(x)=qx$,则$a,f(a),f(f ...
- MT【54】一道二次函数问题的几何意义
[Rather less, but better.]----卡尔·弗里德里希·高斯(1777-1855) (2016诸暨质检18)已知$f(x)=x^2-a|x-1|+b(a>0,b>-1 ...
- MT【39】构造二次函数证明
这种构造二次函数的方法最早接触的应该是在证明柯西不等式时: 再举一例: 最后再举个反向不等式的例子: 评:此类题目的证明是如何想到的呢?他们都有一个明显的特征$AB\ge(\le)C^2$,此时构造二 ...
- MT【37】二次函数与整系数有关的题
解析: 评:两根式是不错的考虑方向,一方面二次函数两根式之前有相应的经验,另一方面这里$\sqrt{\frac{b^2}{4}-c}$正好和两个根有关系.
- MT【322】绝对值不等式
已知 $a,b,c\in\mathbb R$,求证:$|a|+|b|+|c|+|a+b+c|\geqslant |a+b|+|b+c|+|c+a|$ 分析:不妨设$c=\max\{a,b,c\},\d ...
- MT【289】含参绝对值的最大值之三
已知$a>0$,函数$f(x)=e^x+3ax^2-2e x-a+1$,(1)若$f(x)$在$[0,1]$上单调递减,求$a$的取值范围.(2)$|f(x)|\le1$对任意$x\in[0,1 ...
- MT【285】含参数函数绝对值的最大值
(浙江2013高考压轴题)已知$a\in R$,函数$f(x)=x^3-3x^2+3ax-3a+3$(2)当$x\in[0,2]$时,求$|f(x)|$的最大值. 分析:由题意$f^{'}(x)=3x ...
- MT【270】含参绝对值函数最大之二
已知$f(x)=2ax\cos^2x+(a-1)\cos x-1,a>0$,记$|f(x)|$的最大值为$A$,1)求A.2)证明:$|-2a\sin 2x+(1-a)\sin x|\le 2A ...
随机推荐
- c语言第三例
标准的输入输出函数: putchar(输出字符) getchar(获取输入字符) printf(格式输出) scanf(格式输入) puts(输出字符串) gets(获取输入字符串) #include ...
- 分布式理论——quorum原理
编者按:本篇文章是网上一些文章的合集,并不是原创,谢谢各位的分享. 一.基于Quorum投票的冗余控制算法 Quorom 机制,是一种分布式系统中常用的,用来保证数据冗余和最终一致性的投票算法,其主要 ...
- Your ApplicationContext is unlikely to start due to a @ComponentScan of the default package
1.在搭建SpringBoot框架时碰到的问题. ** WARNING ** : Your ApplicationContext is unlikely to start due to a @Comp ...
- Luogu P1494 [国家集训队]小Z的袜子
比较简单的莫队题,主要是为了熟练板子. 先考虑固定区间时我们怎么计算,假设区间\([l,r]\)内颜色为\(i\)的袜子有\(cnt_i\)只,那么对于颜色\(i\)来说,凑齐一双的情况个数为: \( ...
- [朴智妍][Lullaby]
歌词来源:http://music.163.com/#/song?id=484056971 作曲 : Bum/Sophiya/김용신 [作曲 : Bum/Sophiya/k/gi-myong-xin] ...
- 个人博客week2
1. 是否需要有代码规范 对于是否需要有代码规范,请考虑下列论点并反驳/支持: 这些规范都是官僚制度下产生的浪费大家的编程时间.影响人们开发效率, 浪费时间的东西. 我是个艺术家,手艺人,我有自己的规 ...
- Timer定时执行
//定时器 public void timeTask(String hh,int n) {//hh="8:30:00",n=12 Timer timer = new Timer() ...
- 剑指offer:变态跳台阶
题目描述 一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级.求该青蛙跳上一个n级的台阶总共有多少种跳法. 思路 首先想到的解决方案是根据普通跳台阶题目改编,因为可以跳任意级,所以要 ...
- Maven入门指南④:仓库
1 . 仓库简介 没有 Maven 时,项目用到的 .jar 文件通常需要拷贝到 /lib 目录,项目多了,拷贝的文件副本就多了,占用磁盘空间,且难于管理.Maven 使用一个称之为仓库的目录,根据构 ...
- 9-Python3从入门到实战—基础之条件控制语句
Python从入门到实战系列--目录 条件判断 if 条件判断 if 语句语法 if <条件判断1>: <执行1> elif <条件判断2>: <执行2> ...
