HOG参数简介及Hog特征维数的计算（转）

HOG构造函数

CV_WRAP HOGDescriptor() :winSize(64,128), blockSize(16,16), blockStride(8,8),      cellSize(8,8),nbins(9), derivAperture(1), winSigma(-1), histogramNormType(HOGDescriptor::L2Hys),L2HysThreshold(0.2), gammaCorrection(true), nlevels(HOGDescriptor::DEFAULT_NLEVELS)

{}

CV_WRAP HOGDescriptor(Size_winSize, Size _blockSize, Size _blockStride,                 Size _cellSize, int _nbins, int_derivAperture=1, double _winSigma=-1, int _histogramNormType=HOGDescriptor::L2Hys,double _L2HysThreshold=0.2, bool _gammaCorrection=false, int_nlevels=HOGDescriptor::DEFAULT_NLEVELS) : winSize(_winSize),blockSize(_blockSize), blockStride(_blockStride), cellSize(_cellSize),nbins(_nbins), derivAperture(_derivAperture), winSigma(_winSigma),histogramNormType(_histogramNormType), L2HysThreshold(_L2HysThreshold),gammaCorrection(_gammaCorrection), nlevels(_nlevels)

{}

CV_WRAP HOGDescriptor(const String&filename)

{

load(filename);

}

HOGDescriptor(const HOGDescriptor& d)

{

d.copyTo(*this);

}

我们看到HOGDescriptor一共有4个构造函数，前三个有CV_WRAP前缀，表示它们是从DLL里导出的函数，即我们在程序当中可以调用的函数。

HOG基本概念

在构造函数中，有几个参数非常重要，分别为winSize(64,128),  blockSize(16,16),  blockStride(8,8), cellSize(8,8),  nbins(9)。在此，用几个示意图来表示。

a)       窗口大小winSize

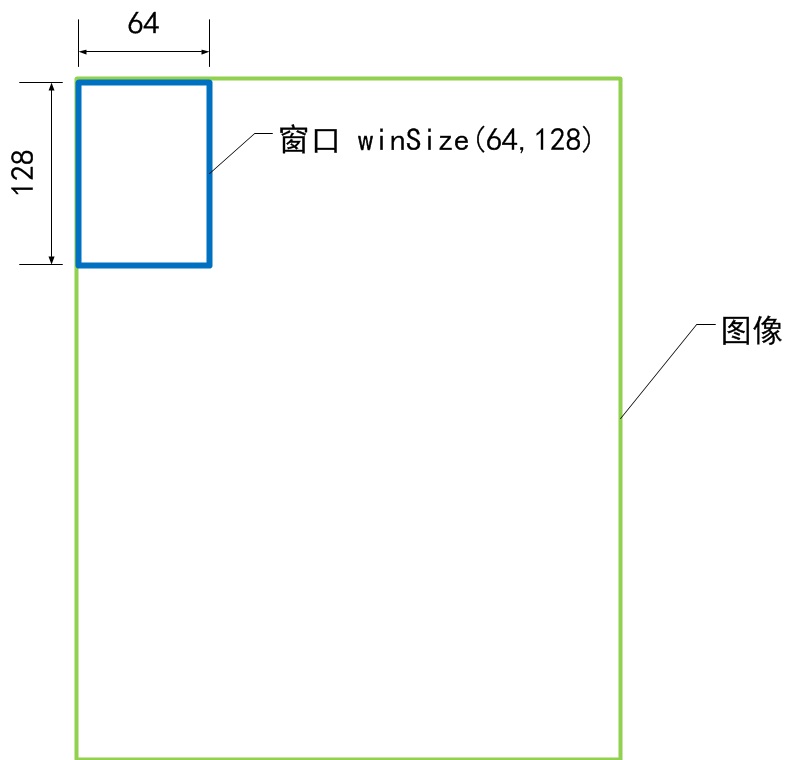
b)      块大小blockSize

c)       胞元大小cellSize

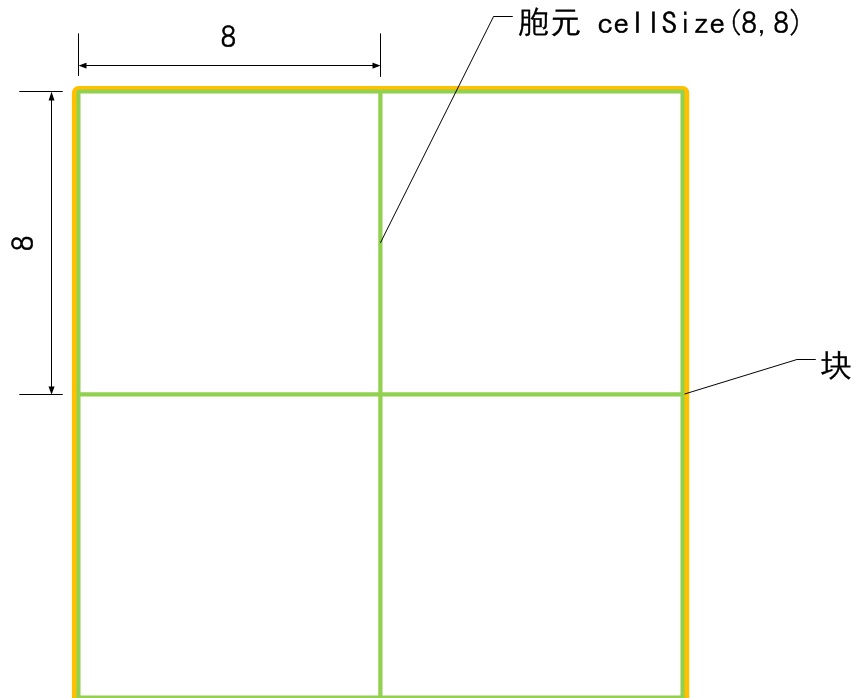
d)       梯度方向数

nbins代表在一个胞元中统计梯度的方向数目。如：nbins=9表示一个胞元内统计9个方向的梯度直方图。

Hog特征维数的计算

首先给出一个hog

HOGDescriptor* hog = newHOGDescriptor(cvSize(64, 48), cvSize(8, 6), cvSize(8, 6), cvSize(4, 3), 9);

根据上面的概念可知，cvSize(64,48)表示窗口的大小，cvSize(8, 6)表示块（block）大小，cvSize(8,6)表示块滑动增量（blockStride）大小，cvSize(4, 3)表示胞元（cell）大小，9表示每个胞单元中梯度直方图的数量。

注：输入的图片尺寸为640×480。

据此，可知：

一个块（block）包含A=(blockSize.width/cellSize.width)*(blockSize.height / cellSize.height)个胞元（cell），所以一个块（block）含有9A个梯度直方图。按照所给出的数据，可得结果为36。

一个窗口包含B=((windowSize.width-blockSize.width)/(blockStrideSize.width)+1)* ((windowSize.height-blockSize.height)/(blockStrideSize.height)+1)个块（block），所以一个窗口包含9AB个梯度直方图。

按照所给出的数据，可得结果为2304。

其次，计算特征向量hog->compute(trainImg,descriptors, Size(64, 48), Size(0, 0))

此处，trainImg代表输入的图片（此处尺寸为640×480），descriptors表示保存特征结果的Vector，Size(64,48)表示windows的步进，第四个为padding，用于填充图片以适应大小。

当padding以默认状态Size(0,0)出现，滑动窗口window来计算图片时，

结果不一定为整数。

此时，查看compute()函数发现，其中有一段代码如下：

padding.width = (int)alignSize(std::max(padding.width,0), cacheStride.width);

padding.height = (int)alignSize(std::max(padding.height,0), cacheStride.height);

这段代码就是用来将padding的大小来适应stride的大小。

在我的实例中，由于取得数都事先设计好，都是整数。而当若结果不为整数时，则将其取值为比其大的最小整数。如若padding.width计算为7.8时，就取8.

所以一幅640×480的图片，按照前面的参数，则可以取的特征数为230400维。

在此，特别感谢几位，分别为：

http://www.cnblogs.com/tornadomeet/archive/2012/08/15/2640754.html

此篇博文总结了一些网上的参考资料，采用Hog特征训练的流程及对OpenCV中Hog代码进行了解释

http://blog.csdn.net/raocong2010/article/details/6239431

此篇博文对Hog中Block，Cell的概念进行了详细的解释。我此篇博客中的图片来自于这篇博文。非常感谢。

http://gz-ricky.blogbus.com/logs/85326280.html

此篇博文对Hog中的特征个数计算进行了详细的解释