04-树5 Root of AVL Tree

平衡二叉树

LL RR LR RL 注意画图理解法

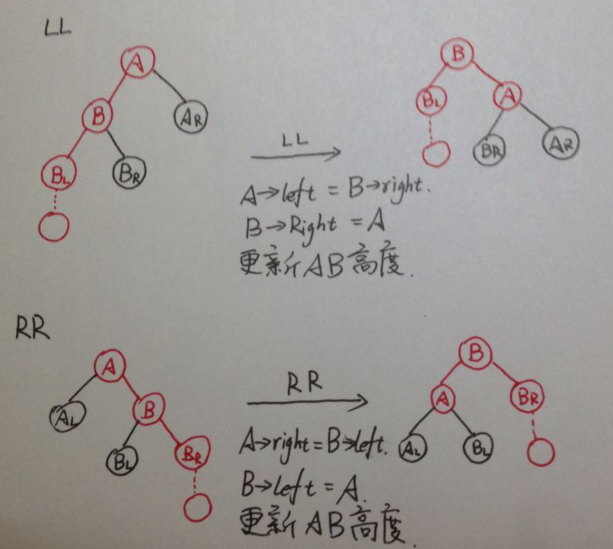
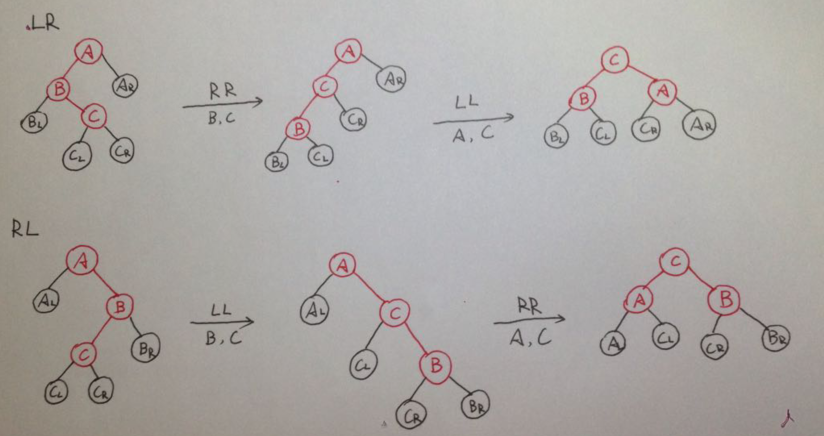
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

70

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

88

 //平衡二叉树 AVL
 #include <stdio.h>
 #include <stdlib.h>

 typedef int ElementType;

 typedef struct AVLNode *Position;
 typedef Position AVLTree; /* AVL树类型 */
 typedef struct AVLNode{
     ElementType data; /* 结点数据 */
     AVLTree left;     /* 指向左子树 */
     AVLTree right;    /* 指向右子树 */
     int height;       /* 树高 */
 };

 int Max ( int a, int b )
 {
     return a > b ? a : b;
 }

 int GetHeight( Position p )
 {
     if(!p)
         return -;
     return p->height;
 }

 /* 将A与B做左单旋，更新A与B的高度，返回新的根结点B */
 /* 注意：A必须有一个左子结点B */
 AVLTree SingleLeftRotation ( AVLTree A )
 {
     AVLTree B = A->left;
     A->left = B->right;
     B->right = A;
     A->height = Max( GetHeight(A->left), GetHeight(A->right) ) + ;
     B->height = Max( GetHeight(B->left), A->height ) + ;

     return B;
 }
 /* 将A与B做右单旋，更新A与B的高度，返回新的根结点B */
 /* 注意：A必须有一个右子结点B */
 AVLTree SingleRightRotation ( AVLTree A )
 {
     AVLTree B = A->right;
     A->right = B->left;
     B->left = A;
     A->height = Max( GetHeight(A->left), GetHeight(A->right) ) + ;
     B->height = Max( A->height, GetHeight(B->right) ) + ;

     return B;
 }

 /* 注意：A必须有一个左子结点B，且B必须有一个右子结点C */
 /* 将A、B与C做两次单旋，返回新的根结点C */
 AVLTree DoubleLeftRightRotation ( AVLTree A )
 {
     /* 将B与C做右单旋，C被返回 */
     A->left = SingleRightRotation(A->left);
     /* 将A与C做左单旋，C被返回 */
     return SingleLeftRotation(A);
 }

 /* 将A、B与C做两次单旋，返回新的根结点C */
 /* 注意：A必须有一个右子结点B，且B必须有一个左子结点C */
 AVLTree DoubleRightLeftRotation ( AVLTree A )
 {
     /* 将B与C做右单旋，C被返回 */
     A->right = SingleLeftRotation(A->right);
     /* 将A与C做左单旋，C被返回 */
     return SingleRightRotation(A);
 }

 /* 将X插入AVL树T中，并且返回调整后的AVL树 */
 AVLTree Insert( AVLTree T, ElementType X )
 {
     if ( !T ) { /* 若插入空树，则新建包含一个结点的树 */
         T = (AVLTree)malloc(sizeof(struct AVLNode));
         T->data = X;
         T->height = ;
         T->left = T->right = NULL;
     } /* if (插入空树) 结束 */

     else if ( X < T->data ) {
         T->left = Insert( T->left, X);/* 插入T的左子树 */
         if ( GetHeight(T->left)-GetHeight(T->right) ==  ) /* 如果需要左旋 */
             if ( X < T->left->data )
                T = SingleLeftRotation(T);      //左单旋 LL
             else
                T = DoubleLeftRightRotation(T); //左-右双旋LR
     } /* else if (插入左子树) 结束 */

     else if ( X > T->data ) {
         T->right = Insert( T->right, X );/* 插入T的右子树 */
         if ( GetHeight(T->left)-GetHeight(T->right) == - )/* 如果需要右旋 */
             if ( X > T->right->data )
                T = SingleRightRotation(T);     //右单旋 RR
             else
                T = DoubleRightLeftRotation(T); //右-左双旋 RL
     } /* else if (插入右子树) 结束 */

     /*else X == T->Data，无须插入 */
     T->height = Max( GetHeight(T->left), GetHeight(T->right) ) + ;    //更新树高 

     return T;
 }

 int main()
 {
     int N, data;
     AVLTree T;
     scanf("%d",&N);
     for(int i = ; i < N; i++) {
         scanf("%d",&data);
         T = Insert(T,data);
     }
     printf("%d\n",T->data);
     return ;
 }