Cross Validation done wrong

Cross validation is an essential tool in statistical learning 1 to estimate the accuracy of your algorithm. Despite its great power it also exposes some fundamental risk when done wrong which may terribly bias your accuracy estimate.

In this blog post I'll demonstrate - using the Python scikit-learn 2framework - how to avoid the biggest and most common pitfall of cross validation in your experiments.

Theory first

Cross validation involves randomly dividing the set of observations intok groups (or folds) of approximately equal size. The first fold is treated as a validation set, and the machine learning algorithm is trained on the remaining k-1 folds. The mean squared error is then computed on the held-out fold. This procedure is repeated k times; each time, a different group of observations is treated as a validation set.

This process results in k estimates of the MSE quantity, namely MSE1, MSE2,...MSEk. The cross validation estimate for the MSE is then computed by simply averaging these values:

CV(k)=1/k∑i=1kMSEi

This value is an estimate, say MSE^, of the real MSE and our goal is to make this estimate as accurate as possible.

Hands on

Let's now have a look at one of the most typical mistakes when using cross validation. When cross validation is done wrong the result is that MSE^ does not reflect its real value MSE. In other words, you may think that you just found a perfect machine learning algorithm with incredibly low MSE, while in reality you simply wrongly applied CV.

I'll first show you - hands on - a wrong application of cross validation and then we will fix it together. The code is also available as an IPython notebook on github.

Dataset generation

# Import pandas

import pandas as pd

from pandas import *

# Import scikit-learn

from sklearn.linear_model import LogisticRegression

from sklearn.cross_validation import *

from sklearn.metrics import *

import random

To make things simple let's first generate some random data and let's pretend that we want to build a machine learning algorithm to predict the outcome. I'll first generate a dataset of 100 entries. Each entry has10.000 features. But, why so many? Well, to demonstrate our issue I need to generate some correlation between our inputs and output which is purely casual. You'll understand the why later in this post.

features = np.random.randint(0,10,size=[100,10000])

target = np.random.randint(0,2,size=100)

df = DataFrame(features)

df['target'] = target

df.head()

Feature selection

At this point we would like to know what are the features that are more useful to train our predictor. This is called feature selection. The simplest approach to do that is to find which of the 10.000 features in our input is mostly correlated the target. Using pandas this is very easy to do thanks to the corr() function. We run corr() on our dataframe, we order the correlation values, and we pick the first two features.

corr = df.corr()['target'][df.corr()['target'] < 1].abs()

corr.sort(ascending=False)

corr.head()

# 3122 0.392430

# 830 0.367405

# 8374 0.351462

# 9801 0.341806

# 5585 0.336950

# Name: target, dtype: float64

Start the training

Great! Out of the 10.000 features we have been able to select two of them, i.e. feature number 3122 and 830 that have a 0.36 and 0.39correlation with the output. At this point let's just drop all the other columns and use these two features to train a simpleLogisticRegression. We then use scikit-learn cross_val_score to compute MSE^ which in this case is equal to 0.33. Pretty good!

features = corr.index[[0,1]].values

training_input = df[features].values

training_output = df['target']

logreg = LogisticRegression()

# scikit learn return the negative value for MSE

# http://stackoverflow.com/questions/21443865/scikit-learn-cross-validation-negative-values-with-mean-squared-error

mse_estimate = -1 * cross_val_score(logreg, training_input, training_output, cv=10, scoring='mean_squared_error')

mse_estimate

# array([ 0.45454545, 0.27272727, 0.27272727, 0.5 , 0.4 ,

# 0.2 , 0.2 , 0.44444444, 0.33333333, 0.22222222])

DataFrame(mse_estimate).mean()

# 0 0.33

# dtype: float64

Knowledge leaking

According to the previous estimate we built a system that can predict a random noise target from a random noise input with a MSE of just0.33. The result is, as you can expect, wrong. But why?

The reason is rather counterintuitive and this is why this mistake is so common3. When we applied the feature selection we used information from both the training set and the test sets used for the cross validation, i.e. the correlation values. As a consequence our LogisticRegressionknew information in the test sets that were supposed to be hidden to it. In fact, when you are computing MSEi in the i-th iteration of the cross validation you should be using only the information on the training fold, and nothing should come from the test fold. In our case the model did indeed have information from the test fold, i.e. the top correlated features. I think the term knowledge leaking express this concept fairly well.

The schema that follows shows you how the knowledge leaked into theLogisticRegression because the feature selection has been appliedbefore the cross validation procedure started. The model knows something about the data highlighted in yellow that it shoulnd't know, its top correlated features.

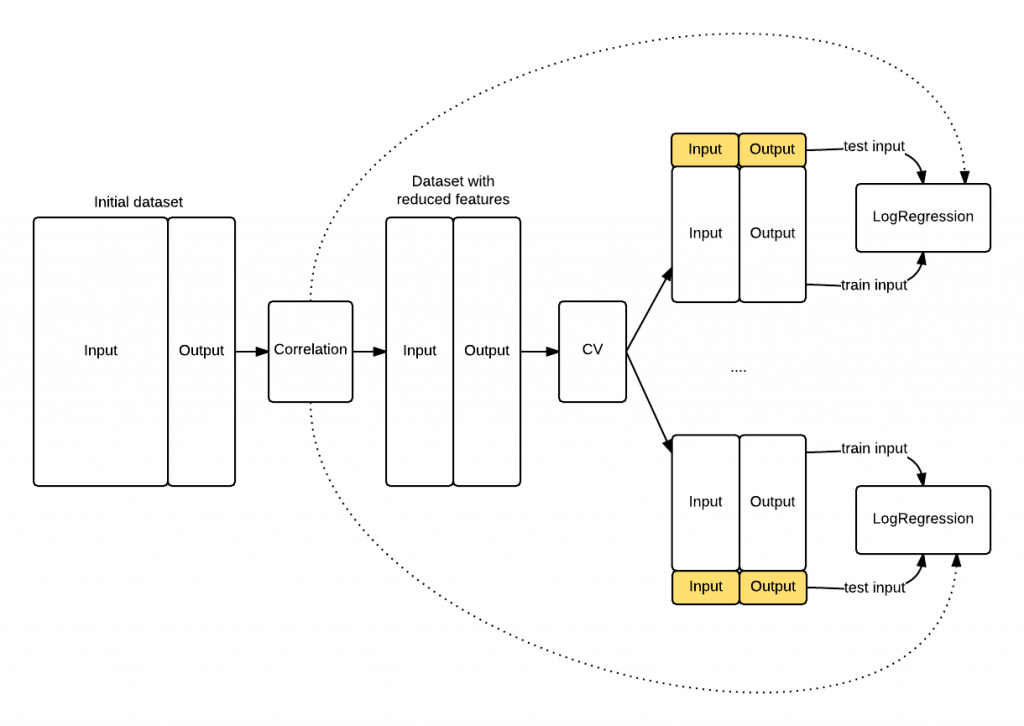Figure 1. The exposed knowledge leaking. The LogisticRegression knows the top correlated features of the entire dataset (hence including test folds) because of the initial correlation operation, whilst it should be exposed only to the training fold information.

Proof that our model is biased

To check that we were actually wrong let's do the following:
* Take out a portion of the data set (take_out_set).
* Train the LogisticRegression on the remaining data using the same feature selection we did before.
* After the training is done check the MSE on the take_out_set.

Is the MSE on the take_out_set similar to the MSE^ we estimated with the CV? The answer is no, and we got a much more reasonable MSE of0.53 that is much higher than the MSE^ of 0.33.

take_out_set = df.ix[random.sample(df.index, 30)]

training_set = df[~(df.isin(take_out_set)).all(axis=1)]

corr = training_set.corr()['target'][df.corr()['target'] < 1].abs()

corr.sort(ascending=False)

features = corr.index[[0,1]].values

training_input = training_set[features].values

training_output = training_set['target']

logreg = LogisticRegression()

logreg.fit(training_input, training_output)

# LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,

# intercept_scaling=1, max_iter=100, multi_class='ovr',

# penalty='l2', random_state=None, solver='liblinear', tol=0.0001,

# verbose=0)

y_take_out = logreg.predict(take_out_set[features])

mean_squared_error(take_out_set.target, y_take_out)

# 0.53333333333333333

Cross validation done right

In the previous section we have seen that if you inject test knowledge in your model your cross validation procedure will be biased. To avoid this let's compute the features correlation during each cross validation batch. The difference is that now the features correlation will use only the information in the training fold instead of the entire dataset. That's the key insight causing the bias we saw previously. The following graph shows you the revisited procedure. This time we got a realistic MSE^ of0.53 that confirms the data is randomly distributed.

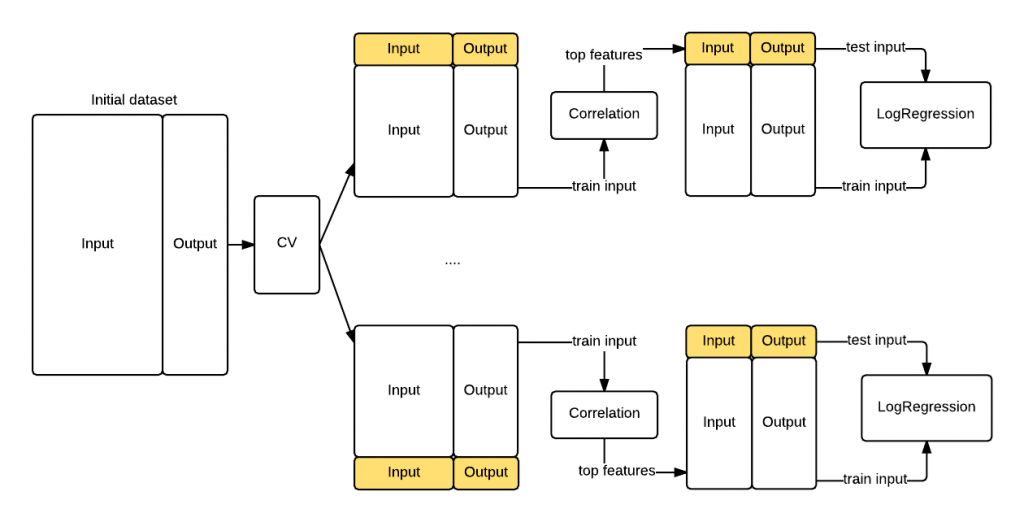Figure 2. Revisited cross validation workflow with the correlation step performed for each of the K train/test folds.

kf = KFold(df.shape[0], n_folds=10)

mse = []

fold_count = 0

for train, test in kf:

print("Processing fold %s" % fold_count)

train_fold = df.ix[train]

test_fold = df.ix[test]

# find best features

corr = train_fold.corr()['target'][train_fold.corr()['target'] < 1].abs()

corr.sort(ascending=False)

features = corr.index[[0,1]].values

# Get training examples

train_fold_input = train_fold[features].values

train_fold_output = train_fold['target']

# Fit logistic regression

logreg = LogisticRegression()

logreg.fit(train_fold_input, train_fold_output)

# Check MSE on test set

pred = logreg.predict(test_fold[features])

mse.append(mean_squared_error(test_fold.target, pred))

# Done with the fold

fold_count += 1

print(DataFrame(mse).mean())

# Processing fold 0

# Processing fold 1

# Processing fold 2

# Processing fold 3

# Processing fold 4

# Processing fold 5

# Processing fold 6

# Processing fold 7

# Processing fold 8

# Processing fold 9

DataFrame(mse).mean()

# 0 0.53

# dtype: float64

Conclusion

We have seen how doing features selection at the wrong step can terribly bias the MSE estimate of your machine learning algorithm. We have also seen how to correctly apply cross validation by simply moving one step down the features selection such that the knowledge from the test data does not leak in our learning procedure.

If you want to make sure you don't leak info across the train and test set scikit learn gives you additional extra tools like the feature selection pipeline 4 and the classes inside the feature selection module 5.

Finally, if you want know more about cross validation and its tradeoffs both R. Kohavi6 and Y. Bengio with Y. Grandvalet7 wrote on this topic.

If you liked this post you should consider following me on twitter.
Let me know your comments!

References

Posted onJuly 29, 2015Authormottalrd

10 thoughts on “Cross Validation done wrong”

Gael Varoquauxsays:

July 29, 2015 at 1:59 pm

To do feature selection inside a cross-validation loop, you should really be using the feature selection objects inside a pipeline:

http://scikit-learn.org/stable/auto_examples/feature_selection/feature_selection_pipeline.html

http://scikit-learn.org/stable/modules/feature_selection.html

That way you can use the model selection tools of scikit-learn:
http://scikit-learn.org/stable/modules/model_evaluation.html

And you are certain that you won't be leaking info across train and test sets.