UPC 2019年第二阶段我要变强个人训练赛第六场

传送门

A.上学路线

 题目描述
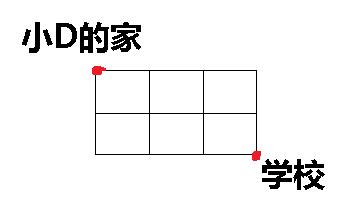
     小D从家到学校的道路结构是这样的：由n条东西走向和m条南北走向的道路构成了一个n*m的网格，每条道路都是单向通行的（只能从北向南，从西向东走）。
     已知小D的家在网格的左上角，学校在网格的右下角。
     问小D从他的家到学校一共有多少种不同的上学路线。
     （配图如下）
 输入
 两个正整数n和m，意义如题目所述。

 输出
 小D上学路线数量，结果对1000000007取余。

题目描述

 样例输入

 样例输出
 

样例输入输出

思路一（递推）：

 ll dp[maxn][maxn];///dp[i][j]:从点(i,j)到(n,m)的路线个数

　　初始化dp[n][m]=1;

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 const int maxn=1e3+;
 #define ll long long
 #define mem(a,b) memset(a,b,sizeof(a))
 const int MOD=;

 int n,m;
 ll dp[maxn][maxn];

 ll Solve()
 {
     mem(dp,);
     for(int i=n;i >= ;--i)
     {
         for(int j=m;j >= ;--j)
         {
             if(i == n && j == m)
                 dp[i][j]=;
             else
                 dp[i][j]=(dp[i+][j]+dp[i][j+])%MOD;
         }
     }
     return dp[][]%MOD;
 }
 int main()
 {
     scanf("%d%d",&n,&m);
     printf("%lld\n",Solve());

     return ;
 }

思路二（记忆化搜索 by mxl）：

　　由题意可知，一共向下走了 n-1 步；

　　那么对于第 i 列可能向下走连续的 0,1,2,...,n-1 步；

ll dp[maxn][maxn];///dp[i][j]:第i列向下走连续的j步含有的总方案数

　　初始化dp为-1；

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 const int maxn=1e3+;
 #define ll long long
 #define mem(a,b) memset(a,b,sizeof(a))
 const int MOD=;

 int n,m;
 ll dp[maxn][maxn];///dp[i][j]:第i列向下走连续的j步含有的总方案数

 ll DFS(int cur,int cnt)///第cur列最多向下走cnt步
 {
     if(cur > m)
         return cnt ==  ? :;

     if(dp[cur][cnt] != -)///记忆化搜索
         return dp[cur][cnt];

     ll ans=;
     for(int i=;i <= cnt;++i)///第cur列向下走i步
         ans=(ans+DFS(cur+,cnt-i))%MOD;

     dp[cur][cnt]=ans;
     return ans;
 }
 ll Solve()
 {
     mem(dp,-);
     return DFS(,n-)%MOD;
 }
 int main()
 {
     scanf("%d%d",&n,&m);
     printf("%lld\n",Solve());

     return ;
 }