本文继续来讨论另一种分类模型————fisher线性判别分析

一、模型思想

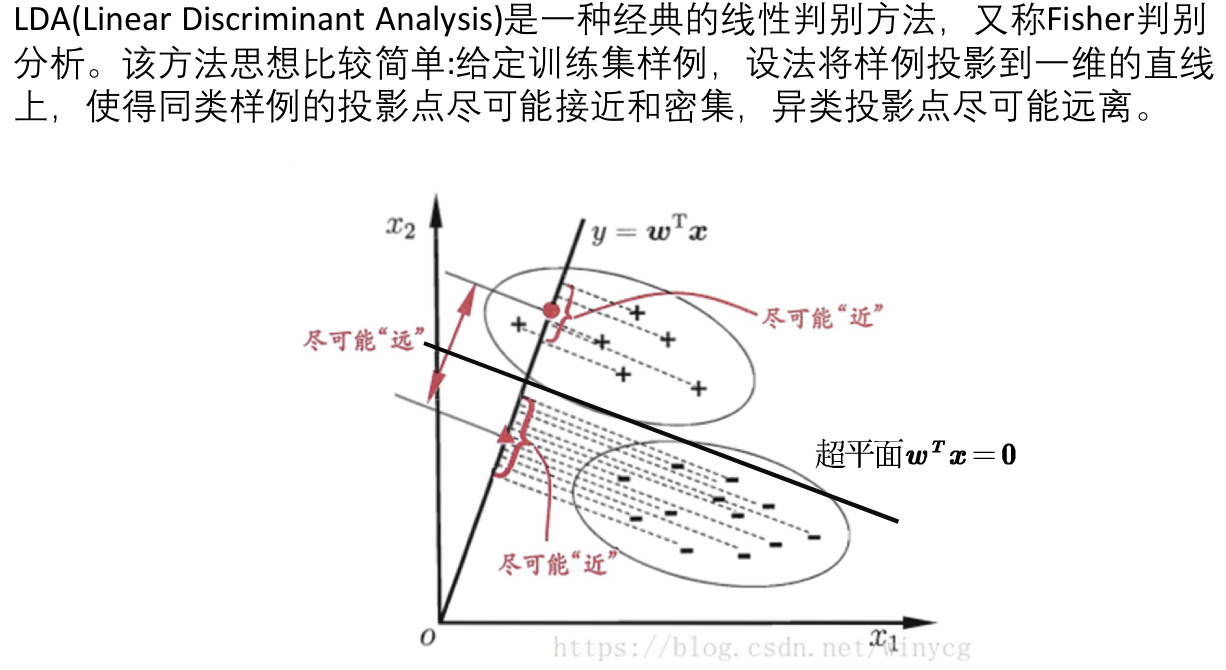
我们以二分类问题举例，在二维平面中我们需要找到一个直线，这个直线需要满足两个使命：

（1）使得同类样例的投影点尽可能接近和密集（2）异类投影点尽可能远离。



二、SPSS的实现

此处我们还是以水果二分类的数据为例

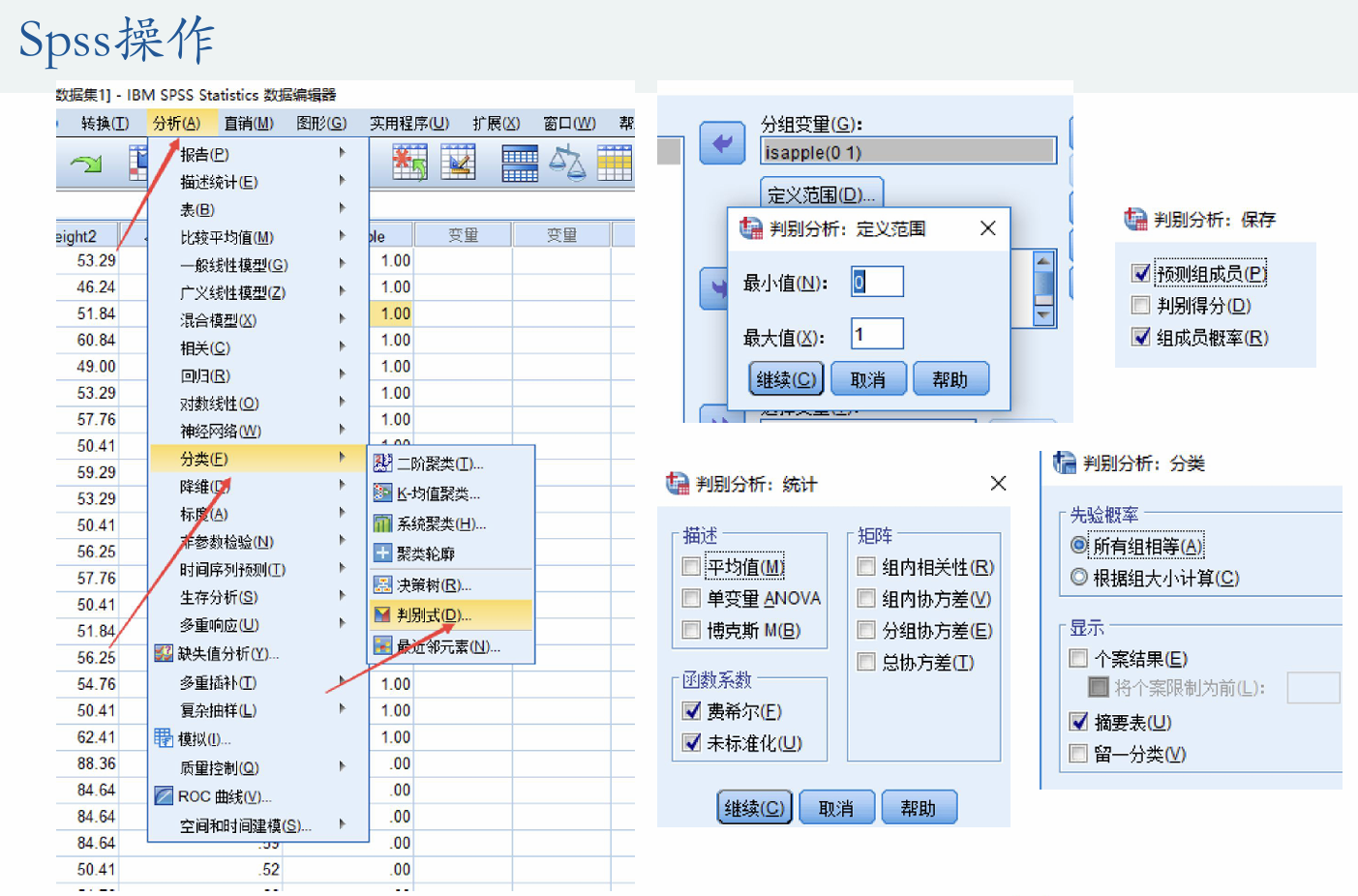
1.参数设置

（1）定义范围

也就是设置分类的类别，如果是二分类就设置0-1，多分类可设置为1-n

(2) 统计

这里需要勾选费希尔系数和未标准化

其中费希尔系数为标准化后的系数，但是我们用未标准化的系数比较多

（3）保存与分类

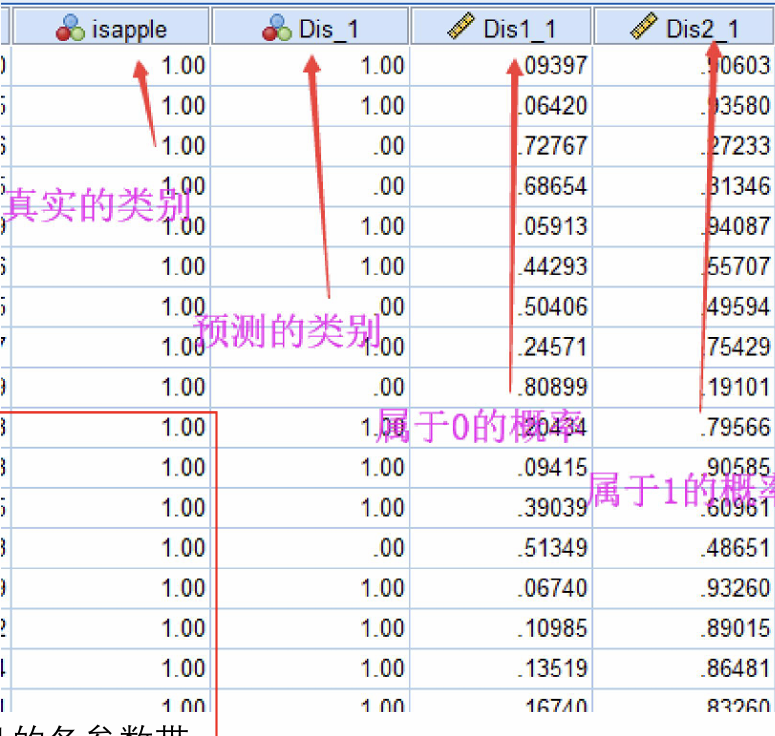
保存即在原始数据增加一个新的变量，此处我们只需要选择概率与组成员即可。概率就是分类为某个类别的概率，组成员就是分类结果



分类的参数我们只需要勾选摘要表即可

2.结果分析

（1）典则判别函数系数

该表就是为标准化的系数，也就是w的值

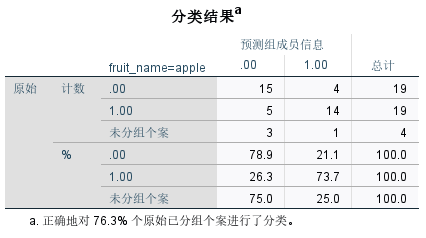
（2）分类结果

分类结果也就是分类的准确率，在主对角线上的值就是预测正确的个数

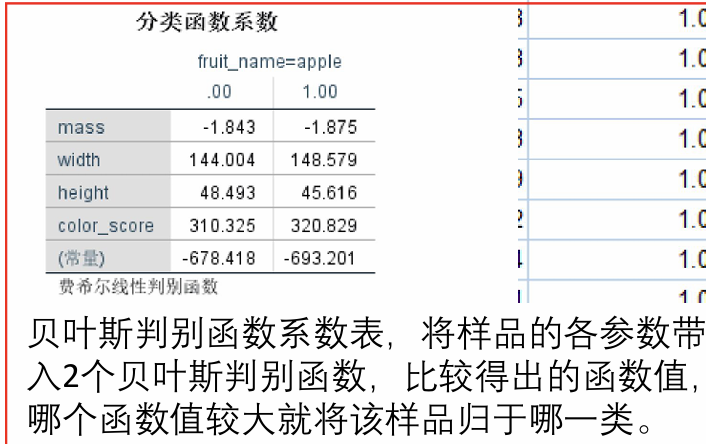
（3）分类函数系数

由于是二分类，会得出两个函数，把原始数据带入两个函数，谁的函数值大，则把该个案分类为这个函数代表的类别

（4）保存预测结果

四、多分类问题

Fisher判别分析可用于多分类问题，模型思想与二分类相似，把二维平面扩展到了n维空间。

实现方法只需要修改一下定义范围即可

同时，Logistic回归也可用于多分类问题，实现方法本文不作叙述，详细步骤请查看清风老师在本章的PPT

fisher线性判别分析和多分类问题探究的更多相关文章

  1. Fisher线性判别分析

    Fisher线性判别分析 1.概述 在使用统计方法处理模式识别问题时,往往是在低维空间展开研究,然而实际中数据往往是高维的,基于统计的方法往往很难求解,因此降维成了解决问题的突破口. 假设数据存在于d ...

  2. 线性判别分析（LDA）准则：FIsher准则、感知机准则、最小二乘（最小均方误差）准则

    准则 采用一种分类形式后,就要采用准则来衡量分类的效果,最好的结果一般出现在准则函数的极值点上,因此将分类器的设计问题转化为求准则函数极值问题,即求准则函数的参数,如线性分类器中的权值向量. 分类器设 ...

  3. 线性判别分析（Linear Discriminant Analysis）转载

    1. 问题 之前我们讨论的PCA.ICA也好,对样本数据来言,可以是没有类别标签y的.回想我们做回归时,如果特征太多,那么会产生不相关特征引入.过度拟合等问题.我们可以使用PCA来降维,但PCA没有将 ...

  4. 线性判别分析算法（LDA）

    1. 问题 之前我们讨论的PCA.ICA也好,对样本数据来言,可以是没有类别标签y的.回想我们做回归时,如果特征太多,那么会产生不相关特征引入.过度拟合等问题.我们可以使用PCA来降维,但PCA没有将 ...

  5. （数据科学学习手札17）线性判别分析的原理简介&Python与R实现

    之前数篇博客我们比较了几种具有代表性的聚类算法,但现实工作中,最多的问题是分类与定性预测,即通过基于已标注类型的数据的各显著特征值,通过大量样本训练出的模型,来对新出现的样本进行分类,这也是机器学习中 ...

  6. 机器学习理论基础学习3.2--- Linear classification 线性分类之线性判别分析(LDA)

    在学习LDA之前,有必要将其自然语言处理领域的LDA区别开来,在自然语言处理领域, LDA是隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),是一种处理文档的主题 ...

  7. 线性判别分析（LDA）, 主成分分析(PCA)及其推导【转】

    前言: 如果学习分类算法,最好从线性的入手,线性分类器最简单的就是LDA,它可以看做是简化版的SVM,如果想理解SVM这种分类器,那理解LDA就是很有必要的了. 谈到LDA,就不得不谈谈PCA,PCA ...

  8. 机器学习中的数学-线性判别分析（LDA）, 主成分分析(PCA)

    转:http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html 版权声明: 本文由L ...

  9. 机器学习中的数学(4)-线性判别分析（LDA）, 主成分分析(PCA)

    版权声明: 本文由LeftNotEasy发布于http://leftnoteasy.cnblogs.com, 本文可以被全部的转载或者部分使用,但请注明出处,如果有问题,请联系wheeleast@gm ...

  10. LDA 线性判别分析

    LDA, Linear Discriminant Analysis,线性判别分析.注意与LDA(Latent Dirichlet Allocation,主题生成模型)的区别. 1.引入 上文介绍的PC ...

随机推荐

  1. WEB服务与NGINX（25）- LNMP架构-WEB集群部署phpmyadmin

    目录 1 LNMP架构-WEB集群部署phpmyadmin 1.1 WEB集群架构需求分析 1.2 WEB集群架构环境 1.3 部署mariadb 1.4 部署web服务器nginx 1.5 部署re ...

  2. k8s快捷命令

    查看node使用率: for i in `kubectl get nodes|awk '{print $1}'|sed '1d'`;do  echo "=========>" ...

  3. post请求和get请求区别及其实例

    1.一般我们在浏览器输入一个网址访问网站都是GET请求;在FORM表单中,可以通过设置Method指定提交方式为GET或者POST提交方式,默认为GET提交方式.HTTP定义了与服务器交互的不同方法, ...

  4. u8二次开发再遇问题再总结

    在调用api生成采购入库单时,报错:该操作会造成订单到货和入库同时存在,请重新检查操作!普通采购必有订单,存货[0501-0304-0075]不能手工录入 这是因为:采购入库单单据必须要录入上游单据, ...

  5. Dockerfile-NGINX镜像制作

    1 NGINX镜像制作: 1.1 NGINX-dockerfile FROM centos:7 LABEL maintainer www.chenleilei.net RUN useradd www ...

  6. 开源一站式敏捷测试管理平台 itest(爱测试) 6.6.1 发布，安全升级及新增强

    (一)itest 简介及更新说明 itest 开源敏捷测试管理,testOps 践行者,极简的任务管理,测试管理,缺陷管理,测试环境管理,接口测试5合1,又有丰富的统计分析.可按测试包分配测试用例执行 ...

  7. 一周万星的文本转语音开源项目「GitHub 热点速览」

    上周的热门开源项目让我想起了「图灵测试」,测试者在不知道对面是机器还是人类的前提下随意提问,最后根据对方回复的内容,判断与他们交谈的是人还是计算机.如果无法分辨出回答者是机器还是人类,则说明机器已通过 ...

  8. Qt-ui的简单使用，常用控件（2）

    1  简介 本文主要介绍Qt ui界面的简单使用,介绍一些常用的控件. 参考视频:https://www.bilibili.com/video/BV1XW411x7NU?p=22 2  常用控件 常用 ...

  9. 剑指Offer-62.二叉搜索树的第k个结点(C++/Java)

    题目: 给定一棵二叉搜索树,请找出其中的第k小的结点.例如, (5,3,7,2,4,6,8)    中,按结点数值大小顺序第三小结点的值为4. 分析: 二叉搜索树的中序遍历结果正好是按数值升序排列的结 ...

  10. vs code 中开发 .net5 mvc

    asp.net core mvc ------------ 安装vscode-solution-explorer,C# 2个扩展.遇到yes就点yes. 新建一个文件夹:D:\repos\Net5Mv ...