2021-07-29:最大路径和。给定一个矩阵matrix,先从左上角开始,每一步只能往右或者往下走,走到右下角。然后从右下角出发,每一步只能往上或者往左走,再回到左上角。任何一个位置的数字,只能获得
2021-07-29:最大路径和。给定一个矩阵matrix,先从左上角开始,每一步只能往右或者往下走,走到右下角。然后从右下角出发,每一步只能往上或者往左走,再回到左上角。任何一个位置的数字,只能获得一遍。返回最大路径和。
福大大 答案2021-07-29:
错误的方法:贪心。左上→右下,取最大值。将走过的路变成零。然后右下→左上,取最大值。最后两个最大值相加。这种方法看起来没问题,实际上是错误的。
正确的方法:递归。两个人都从左上→右下。如果走到同一个位置,值只加一次。如果没走到同一个位置,两个值都加。
时间复杂度:?,不好推断。
空间复杂度:O(N+M)。
代码用golang编写。代码如下:
package main
import "fmt"
func main() {
grid := [][]int{
{1, 1, 1, 1, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 0, 0, 0, 0, 1},
{1, 0, 0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 1, 1, 1, 1, 1, 1},
}
ret := cherryPickup(grid)
fmt.Println(ret)
}
func cherryPickup(grid [][]int) int {
return process(grid, 0, 0, 0, 0, 0)
}
func process(grid [][]int, a int, b int, c int, d int, ans int) int {
N := len(grid)
M := len(grid[0])
//走到最右下位置
if a == N-1 && b == M-1 {
return ans + grid[N-1][M-1]
}
temp := 0
//A下B右
if a+1 < N && d+1 < M {
temp = getMax(temp, process(grid, a+1, b, c, d+1, ans))
}
//A下B下
if a+1 < N && c+1 < N {
temp = getMax(temp, process(grid, a+1, b, c+1, d, ans))
}
//A右B右
if b+1 < M && d+1 < M {
temp = getMax(temp, process(grid, a, b+1, c, d+1, ans))
}
//A右B下
if b+1 < M && c+1 < N {
temp = getMax(temp, process(grid, a, b+1, c+1, d, ans))
}
if a == c { //同一个位置,只需要加一次
ans += grid[a][b]
} else { //不同位置,两个位置都需要加一次
ans += grid[a][b]
ans += grid[c][d]
}
return ans + temp
}
func getMax(a int, b int) int {
if a > b {
return a
} else {
return b
}
}
执行结果如下:
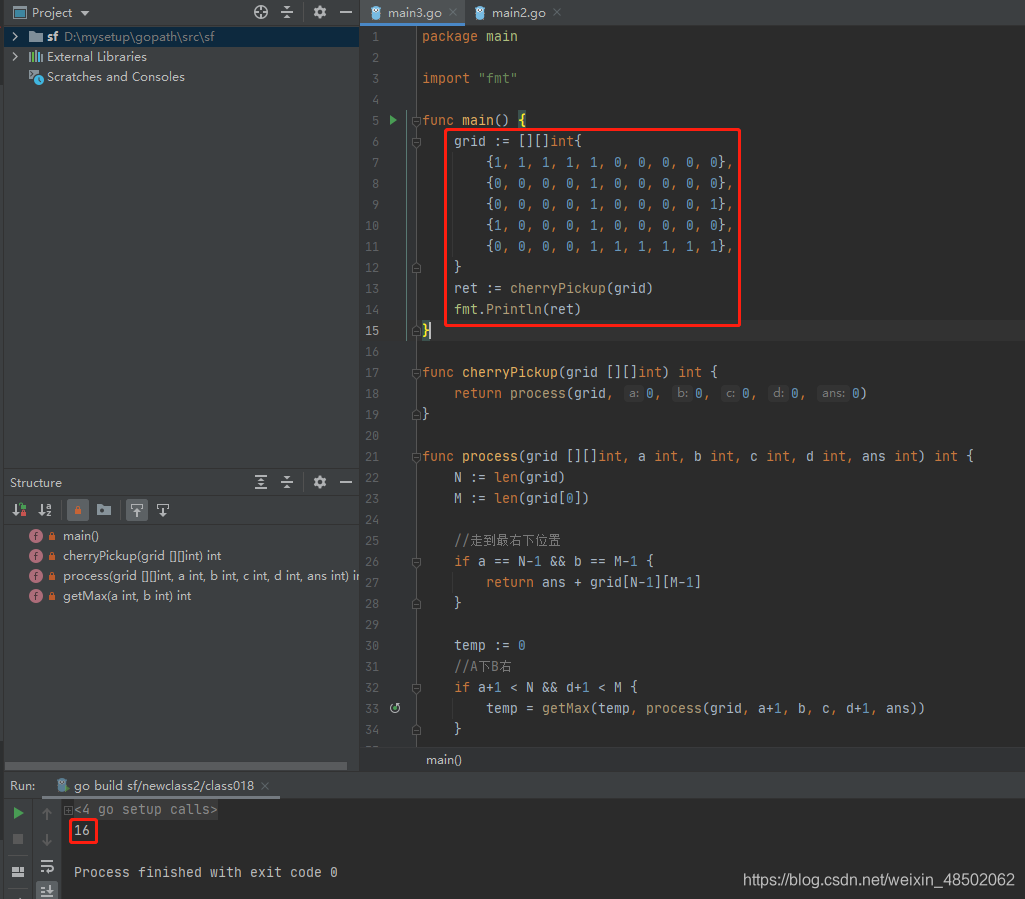
2021-07-29:最大路径和。给定一个矩阵matrix,先从左上角开始,每一步只能往右或者往下走,走到右下角。然后从右下角出发,每一步只能往上或者往左走,再回到左上角。任何一个位置的数字,只能获得的更多相关文章
- 一个n*n 的方格,要从左上角走到右下角,一次只能往右或往下走一步,求算法得出所有走动的方法数。
题目一:一个n*n 的方格,要从左上角走到右下角,一次只能往右或往下走一步,求算法得出所有走动的方法数. 分析:对于第(i,j)个格子,只有向右走一步到达或者向左走一步到达,dp(i,j) = d(i ...
- 2021.07.20 CF1477A Nezzar and Board(最大公因数,未证)
2021.07.20 CF1477A Nezzar and Board(最大公因数,未证) CF1477A Nezzar and Board - 洛谷 | 计算机科学教育新生态 (luogu.com. ...
- ZROI 19.07.29 线性代数入门/wq
1.高斯消元 在模意义下依然有效,对主元求逆即可. 甚至可以模合数,需要对两个方程辗转相除,复杂度\(O(n^3\log p)\). 辗转相除法只要能定义带余除法就有效. 逆矩阵:对于矩阵\(A\), ...
- 2021.10.29 数位dp
2021.10.29 数位dp 1.数字计数 我们先设数字为ABCD 看A000,如果我们要求出它所有数位之和,我们会怎么求? 鉴于我们其实已经求出了0到9,0到99,0到999...上所有数字个数( ...
- 2021.07.17 题解 CF1385E Directing Edges(拓扑排序)
2021.07.17 题解 CF1385E Directing Edges(拓扑排序) CF1385E Directing Edges - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) ...
- 2021.07.09 K-D树
2021.07.09 K-D树 前置知识 1.二叉搜索树 2.总是很长的替罪羊树 K-D树 建树 K-D树具有二叉搜索树的形态,对于每一个分类标准,小于标准的节点在父节点左边,大于标准的节点在父节点右 ...
- 002.Create a web API with ASP.NET Core MVC and Visual Studio for Windows -- 【在windows上用vs与asp.net core mvc 创建一个 web api 程序】
Create a web API with ASP.NET Core MVC and Visual Studio for Windows 在windows上用vs与asp.net core mvc 创 ...
- 最新RabbitMQ安装指南2021.07
一.RabbitMQ入门及安装 1.入门及安装 01 概述 简单概述: RabbitMQ是一个开源的遵循 AMQP协议实现的基于 Erlang语言编写,支持多种客户端(语言),用于在分布式系统中存储消 ...
- 【零碎小bug系列】windows下的回车和换行符,cmd(telnet)上输出不左对齐
cmd(telnet)上输出不左对齐,而是有莫名其妙的空格 目录 cmd(telnet)上输出不左对齐,而是有莫名其妙的空格 背景 解决 细究 背景 在cmd上使用telnet连接本地端口的服务器时, ...
- 2021.10.29 P1649 [USACO07OCT]Obstacle Course S(BFS)
2021.10.29 P1649 [USACO07OCT]Obstacle Course S(BFS) 题意: 给一张n*n的图,起点为A,终点为 B,求从A到B转弯次数最少为多少. 分析: 是否存在 ...
随机推荐
- 使用yarn启用项目,报错无法加载文件 C:\Users\Administrator\AppData\Roaming\npm\yarn.ps1,因为在此系 统上禁止运行脚本。有关详细信息,请参阅 https:/go.microsoft.com/fwlink/?LinkID=135170 中的 about_Execution_Policies。
这是由于新版win10 安装的时候会出现: 解决 搜索powershell,右键以管理员身份运行 2.打开之后,执行命令set-ExecutionPolicy RemoteSigned更改 Power ...
- win10_pyhive链接hive失败,提示:Could not start SASL
win10_pyhive链接hive失败,提示:Could not start SASL https://blog.csdn.net/weixin_45684985/article/details/1 ...
- Linux & 标准C语言学习 <DAY6>
一.数组 什么是数组:变量的组合,是一种批量定义相同类型变量的方式 定义: 类型名 数组名[数量]; int arr[5]; 注意:数 ...
- 在不使用SQL过程化编程的情况下,实现一个条件结构【SQL149 根据指定记录是否存在输出不同情况】
题目地址 https://www.nowcoder.com/practice/f72d3fc27dc14f3aae76ee9823ccca6b 思路 加了3列标记位,来达成目的.不直观而且占用内存,但 ...
- windows作业系统部署nfs服务
文件共享的需求是如何产生的? 据说当年美国和苏联冷战期间,双方都有摧毁对方的能力.而苏联 不怕死的性格让美国人多少有些害怕.美国当时害怕自己的军事指挥中心被苏联摧毁.于是,美国建立了阿帕网,并把自己的 ...
- ArrayBuffer、Float32Array、Uint8Array 详解
ArrayBuffer ArrayBuffer()是一个普通的JavaScript构造函数,可用于在内存中分配特定数量的字节空间. const buf = new ArrayBuffer(16); / ...
- 柏林噪声算法(Perlin Noise)
概述 引述维基百科的介绍: Perlin噪声(Perlin noise,又称为柏林噪声)指由Ken Perlin发明的自然噪声生成算法,具有在函数上的连续性,并可在多次调用时给出一致的数值. 在电子游 ...
- 【命令设计模式详解】C/Java/JS/Go/Python/TS不同语言实现
简介 命令模式(Command Pattern)是一种数据驱动的设计模式,也是一种行为型设计模式.这种模式的请求以命令的形式包裹在对象中,并传给调用对象.调用对象再寻找合适的对象,并把该命令传给相应的 ...
- GET 和 POST 到底有什么区别?
HTTP最早被用来做浏览器与服务器之间交互HTML和表单的通讯协议:后来又被被广泛的扩充到接口格式的定义上.所以在讨论GET和POST区别的时候,需要现确定下到底是浏览器使用的GET/POST还是用H ...
- AIArena Frontend 初步练习
尝试对starter项目的页面进行改变 修改侧边栏,只留下最上面的「仪表盘」和「列表页」两个大模块 in SideNav.vue the code for the sidebar menu is: & ...
