2021-02-14：假设有排成一行的N个位置，记为1~N，N 一定大于或等于 2，开始时机器人在其中的M位置上(M 一定是 1~N 中的一个)。如果机器人来到1位置，那么下一步只能往右来到2位置；如果机器人来到N位置，那么下一步只能往左来到 N-1 位置；如果机器人来到中间位置，那么下一步可以往左走或者往右走；规定机器人必须走 K 步，最终能来到P位置(P也是1~N中的一个)的方法有多少种？

2021-02-14：假设有排成一行的N个位置，记为1~N，N 一定大于或等于 2，开始时机器人在其中的M位置上(M 一定是 1~N 中的一个)。如果机器人来到1位置，那么下一步只能往右来到2位置；如果机器人来到N位置，那么下一步只能往左来到 N-1 位置；如果机器人来到中间位置，那么下一步可以往左走或者往右走；规定机器人必须走 K 步，最终能来到P位置(P也是1~N中的一个)的方法有多少种？给定四个参数 N、M、K、P，返回方法数。

福哥答案2021-02-14：

自然智慧即可。
1.递归。有代码。
两种情况。左移、右移。
2.带dp的递归。有代码。
3.动态规划。有代码。
dp[i][j]，i是机器人位置，j是剩余步数。
dp[i][j]依赖左上和左下。见图。
dp[i][j]=【左上】+【左下】。
4.另一种递归。有代码。

代码用golang编写，代码如下：

package main

import "fmt"

func main() {
    fmt.Println("1.递归：", RobotWalk1(5, 2, 4, 6))
    fmt.Println("2.带dp的递归：", RobotWalk2(5, 2, 4, 6))
    fmt.Println("3.动态规划：", RobotWalk3(5, 2, 4, 6))
    fmt.Println("4.另一种递归：", RobotWalk4(5, 2, 4, 6))
}

func RobotWalk1(N int, start int, aim int, K int) int {
    if N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1 {
        return -1
    }
    return process1(start, K, aim, N)
}

// 机器人当前来到的位置是cur，
// 机器人还有rest步需要去走，
// 最终的目标是aim，
// 有哪些位置？1~N
// 返回：机器人从cur出发，走过rest步之后，最终停在aim的方法数，是多少？
func process1(cur int, rest int, aim int, N int) int {
    if rest == 0 { // 如果已经不需要走了，走完了！
        if cur == aim {
            return 1
        } else {
            return 0
        }
    }
    // (cur, rest)
    if cur == 1 { // 1 -> 2
        return process1(2, rest-1, aim, N)
    }
    // (cur, rest)
    if cur == N { // N-1 <- N
        return process1(N-1, rest-1, aim, N)
    }
    // (cur, rest)
    return process1(cur-1, rest-1, aim, N) + process1(cur+1, rest-1, aim, N)
}

func RobotWalk2(N int, start int, aim int, K int) int {
    if N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1 {
        return -1
    }
    dp := make([][]int, N+1)
    for i := 0; i < N+1; i++ {
        dp[i] = make([]int, K+1)
    }
    for i := 0; i <= N; i++ {
        for j := 0; j <= K; j++ {
            dp[i][j] = -1
        }
    }
    // dp就是缓存表
    // dp[cur][rest] == -1 -> process1(cur, rest)之前没算过！
    // dp[cur][rest] != -1 -> process1(cur, rest)之前算过！返回值，dp[cur][rest]
    // N+1 * K+1
    return process2(start, K, aim, N, dp)
}

// cur 范: 1 ~ N
// rest 范：0 ~ K
func process2(cur int, rest int, aim int, N int, dp [][]int) int {
    if dp[cur][rest] != -1 {
        return dp[cur][rest]
    }
    // 之前没算过！
    ans := 0
    if rest == 0 {
        if cur == aim {
            ans = 1
        } else {
            ans = 0
        }
    } else if cur == 1 {
        ans = process2(2, rest-1, aim, N, dp)
    } else if cur == N {
        ans = process2(N-1, rest-1, aim, N, dp)
    } else {
        ans = process2(cur-1, rest-1, aim, N, dp) + process2(cur+1, rest-1, aim, N, dp)
    }
    dp[cur][rest] = ans
    return ans

}

func RobotWalk3(N int, start int, aim int, K int) int {
    if N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1 {
        return -1
    }
    dp := make([][]int, N+1)
    for i := 0; i < N+1; i++ {
        dp[i] = make([]int, K+1)
    }
    dp[aim][0] = 1
    for rest := 1; rest <= K; rest++ {
        dp[1][rest] = dp[2][rest-1]
        for cur := 2; cur < N; cur++ {
            dp[cur][rest] = dp[cur-1][rest-1] + dp[cur+1][rest-1]
        }
        dp[N][rest] = dp[N-1][rest-1]
    }
    return dp[start][K]
}

//递归
func RobotWalk4(N int, start int, aim int, K int) int {
    ansVal := 0
    ans := &ansVal
    process4(N, start, K, aim, ans)
    return *ans
}

//N个位置，固定
//M是起始位置
//K步
//P是最终位置，固定
func process4(N int, M int, K int, P int, ans *int) {
    if M < 1 || M > N {
        return
    }
    if K == 0 {
        if M == P {
            *ans++
        }
        return
    }
    process4(N, M-1, K-1, P, ans)
    process4(N, M+1, K-1, P, ans)

}

　　

执行结果如下：

***
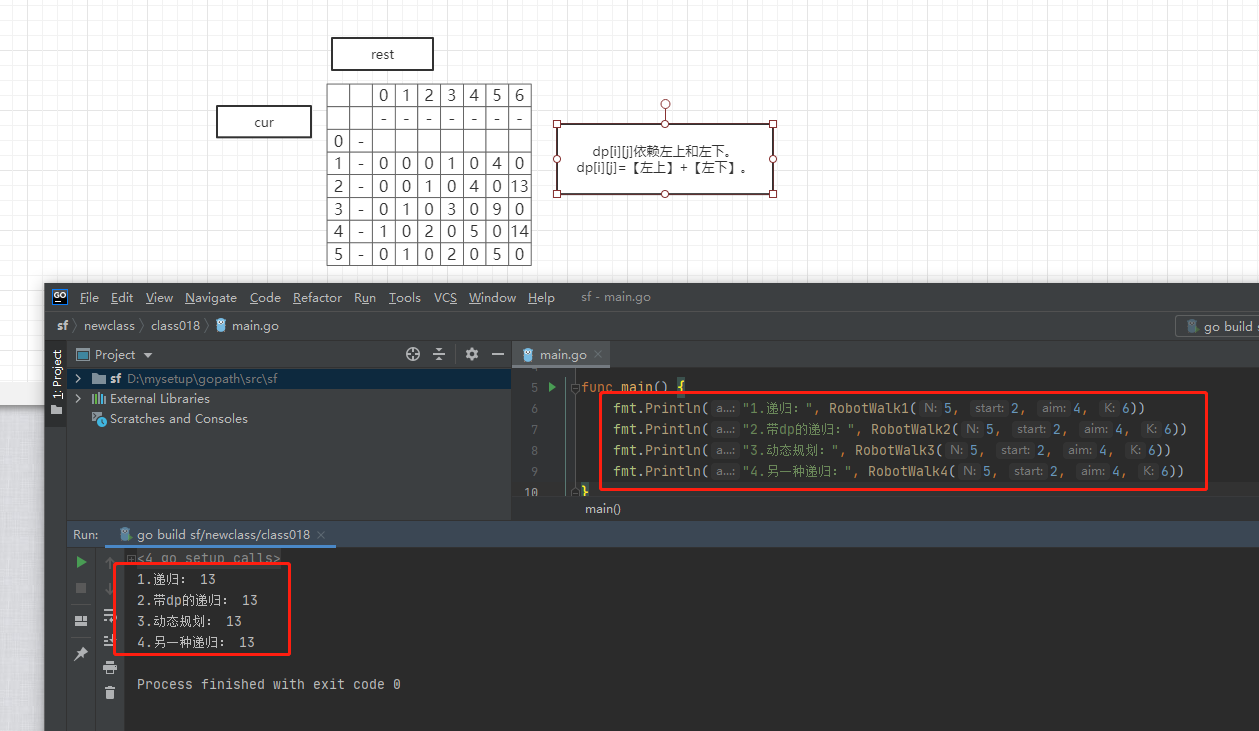
[左神java代码](https://github.com/algorithmzuo/algorithmbasic2020/blob/master/src/class18/Code01_RobotWalk.java)
[评论](https://user.qzone.qq.com/3182319461/blog/1613259761)