结论&定理大全

定理 1：包含 \(0\) 与 \(2^k-1\) 的按位与或空间和 \(k\) 个点的有传递性的有向图形成双射

证明：

空间->传递闭包：对于任意两个位 \(i,j\)，若某个数包含 \(i\)，则它一定包含 \(j\)，则连边 \((i,j)\)。

传递闭包->空间：对于每条边 \((i,j)\)，令第 \(i\) 位为 \(1\) 而第 \(j\) 位为 \(0\) 的数为不合法，则所求空间为所有合法的数。

前一个弄出来的显然是传递闭包。下证后一个是个空间：

考虑这个有向图的所有闭合子图，可以发现闭合子图的与/或都是闭合子图，于是与和或都表示出来了，证毕。

定理 2：对于一张带权无向图，设 1 号点度数为 \(k\) 时的最小生成树权值和为 \(f(k)\)，则 \(f(k)\) 下凸

证明：

先把最小生成树建出来，设此时 1 号点度数为 \(k_0\)。下面考虑 \(k>k_0\) 时的情况（\(k<k_0\) 类似）

令一次“增交换”为加一条 1 边、去掉一条非 1 边，一次“减交换”为去掉一条 1 边、加一条非 1 边。

设 \(k-k_0=a\)，那么从最小生成树开始，我们要进行 \(a+t\) 次“增交换”， \(t\) 次“减交换”。显然可以不妨设各个交换间互不相交。

那么我们发现如果只进行其中的 \(t\) 次“增交换”和 \(t\) 次“减交换”，则由原最小生成树的最小性，进行这些交换并不会变优。于是只会进行 \(a\) 次“增交换”，不会进行“减交换”。

那每次进行的“增交换”一定是排序后当前价值最小的交换，那凸性即可得证。同时可以证明当 \(k\) 递增时 1 边是一条条增加的。

定理 3：对于停时问题，如果状态转移形成 DAG，则停时期望为所有非法状态出现的概率 * 离开这个状态的期望时间

证明：

考虑停时期望为所有初始节点 S 到终止节点 T 的路径出现的概率 * 其期望时间，根据期望的线性性，一条路径上的期望时间可以视为所有点走出来的期望时间之和（这么说不准确，应该是整个道路网放在一起考虑），于是大概算一算就可以得出。

也可以将路径分为 \(S\rightarrow u\) 与 \(u\rightarrow T\) 两段来考虑。

定理 4.0：强连通竞赛图一定有哈密顿回路，竞赛图一定有哈密顿路

定理 4.1：一个竞赛图强联通当且仅当把点按出度排序后不存在 \(k<n\) 使得前 \(k\) 个点的出度之和是 \(k \choose 2\)

定理 4.2：\(n \geq 3\) 的强连通竞赛图必定有长度为 \(n-1\) 中所有长度的哈密顿路径（从而也有 \([3,n]\) 中所有的长度）

定理 4.3：\(n>3\) 的强连通竞赛图必定有大小 \(<n\) 的（所有大小的）强连通子图（也是竞赛图）

证明：

4.1 图不强连通 \(\Leftrightarrow\) 有一个大小为 \(k\) 的块封闭着出不去 \(\Leftrightarrow\) 这个块出度和为 \(k \choose 2\)

4.2 归纳证明：随便挖掉一个点 \(u\)，图可能变成 \(A \rightarrow B \rightarrow C \rightarrow u \rightarrow A\)，由归纳假设可以从 \(A\) 中挖掉一个点

继续归纳就知道 \([3,n]\) 都有

4.3 有哈密顿回路不就是强连通子图了吗

定理 5：若 \(\sum i c_i=n\)，则 \(\sum \log c_i = O(\sqrt{n})\)

推论：\(\sum a_i=n\) 的背包问题，进行二进制分组，其复杂度为 \(O(n\sqrt{n})\)

证明 1：（\(\textcolor{red}{\texttt{W}}\textcolor{black}{\texttt{u\_Ren}}\)）

\[\sum_i \log c_i = \sum_i \sum\limits_{j=1}^{c_i} {1\over j}
\]

这等价于有 \(i\) 种物品，你一共可以挑 \(n\) 个，每当你挑出第 \(i\) 个物品，所获得的收益为 \(1\over j\)（\(j\) 为到目前为止已经挑出的该种物品数量），付出的代价为 \(i\)，求付出总代价为 \(n\) 时的最大收益。

于是总收益最大值为

\[\begin{aligned}
&\ \frac{1}{1\times 1}+\frac{1}{1\times 2}+\frac{1}{2\times 1}+\frac{1}{1\times 3}+\frac{1}{3\times 1}+\frac{1}{1\times 4}+\frac{1}{2\times 2}+\frac{1} {4\times 1}+\dots \\
= &\ \frac{1}{a_1\times b_1}+\frac{1}{a_2\times b_2}+\frac{1}{a_3\times b_3}+\dots \\
\leq &\ \frac{1}{a_1+b_1-1}+\frac{1}{a_2+b_2-1}+\frac{1}{a_3+b_3-1}+\dots \\
\leq &\ \frac{1}{1}+\frac{1}{2}+\frac{1}{2}+\frac{1}{3}+\frac{1}{3}+\frac{1}{3}+\dots \\
= &\ 1\times \frac{1}{1}+2\times \frac{1}{2}+\dots+\sqrt{n}\times \frac{1}{\sqrt{n}} \\
= &\ \sqrt{n}
\end{aligned}
\]

证毕。

证明 2：（\(\textcolor{red}{\texttt{p}}\textcolor{black}{\texttt{\_b\_p\_b}}\)）

设 \(d_i=ic_i\)，则有

\[\begin{aligned}
& \sum \log c_i \\
= & \sum \log {d_i \over i} \\
= & \sum \log d_i -\sum \log i \\
\end{aligned}
\]

而有

\[(\log (\frac{x}{i}+1))'={1\over x+i}
\]

故当 \(d_1+1=d_2+2=\dots=d_{\sqrt{n}}+\sqrt{n}\) 时，\(\sum \log d_i\) 有最大值，此时有 \(d_i=\sqrt{n}-i\) ，从而 \(c_i={d_i\over i}={\sqrt{n}\over i}-1\)

因此

\[\begin{aligned}
&\ \sum \log c_i \\
= &\ \sum \log {\sqrt{n}\over i} \\
= &\ \sqrt{n}\log\sqrt{n}- \sum\limits_{i=1}^{\sqrt{n}} \log i\\
= &\ \sqrt{n}\log\sqrt{n}-(\sqrt{n}\log\sqrt{n}-\sqrt{n})\texttt{（积分）}\\
= &\ \sqrt{n}
\end{aligned}
\]

注意这里 \(\sum\limits_{i=1}^{\sqrt{n}} \log i=\sqrt{n}\log\sqrt{n}-\sqrt{n}\) 是不带常数的（p_b_p_b 教的），所以可以这么减掉

定理 6：对于子集卷积重定义的乘法所形成的运算，均可用 FWT 拆开后计算

顺序：先横着做一遍 FWT，然后竖着对每个位置做普通多项式运算（ln，exp 随便），最后再横着做一遍 IFWT。

定理 7：一棵树的点分治（实际）期望复杂度为 \(\sum f(u)\)，其中 \(f(u)\) 为当树以 \(u\) 为根时，所有节点的深度的倒数和，即 \(f(u)=\sum {1\over dep_i}\)

证明：

一棵树点分治的期望复杂度是对于每个节点，其所在连通块存在的期望时间，即以该点为根后，每次删除一个子树，整棵树被删空的期望时间，记为 \(f(u)\)。

整棵树被删空的期望时间即为每个节点自己把自己删掉（而不是删子树时被删掉）的概率和。

考虑我们将 \(n\) 个点摆成一个排列，按顺序删点，如果一个点已经被（删子树时）删掉了就跳过，容易通过“鞭尸”分析发现与删子树等价。

于是一个点自己把自己删掉的概率就是它是从它到根的路径上的所有节点中在排列里第一次出现的概率，即为其深度的倒数。于是 \(f(u)=\sum {1\over dep_i}\)，答案为 \(\sum f(u)\)。

放到仙人掌上也能做，容斥即可。

定理 8：\(\lfloor f(x)\rfloor\) 与 \(\lfloor g(x)\rfloor\) 关系如下

\[\begin{aligned}
& \texttt{let } F(x)=\lfloor f(x)\rfloor,\ G(x)=\lfloor g(x)\rfloor \\
& f(x)\in (-\infty,g(x)-1) \Rightarrow F(x)\ne G(x)\\
& f(x)\in [g(x)-1,g(x)) \Rightarrow F(x)\in \{G(x)-1,G(x)\}\\
& f(x)\in [g(x),g(x)+1) \Rightarrow F(x)\in \{G(x),G(x)+1\}\\
& f(x)\in [g(x)+1,+\infty) \Rightarrow F(x)\ne G(x)
\end{aligned}
\]

定理 9：\(\sum_{p\in Prime} {n\over p}=O(n \log \log n)\) ，即 Dirichlet 前缀和与埃筛的时间复杂度均为 \(O(n \log \log n)\)

证明：

对于任意一个数 \(x\)，其为质数的概率为 \({1\over \pi(x)-\pi(x-1)}=\log x\) ，所以——

\[\begin{aligned}
& \sum_p {n\over p} \\
= & \sum_{i=1}^n \frac{n}{i\cdot [i\in P]} \\
= & \sum_{i=1}^n \frac{n}{i\log i} \\
= & n \sum_{i=1}^n \frac{1}{i\log i} \\
= & n \displaystyle \int_{1}^{n} \frac{1}{x\ln x}dx \\
= & n \cdot [\ln\ln x + C]_{2}^{n} \\
= & n \ln \ln n = O(n \log \log n) \\
\end{aligned}
\]

定理 10：若函数 \(f(n)\) 满足当 \(n\) 为偶数时 \(f(n)=2f({n\over 2})\)，当 \(n\) 为奇数时 \(f(n)=f({n-1\over 2})+f({n+1\over 2})\)，则 \(f(n)\) 可以用记忆化搜索在 \(O(\log n)\) 或 \(O(\log^2 n)\) 的时间内求出

证明：

若 \(n\) 为偶数，则 \(f(n)\) 只会递归到 \(f({n\over 2})\)，显然。

若 \(n\) 为奇数，设 \(u={n-1\over 2}\)，则 \(f(n)\) 递归到 \(f(u)\) 和 \(f(u+1)\)。不妨设 \(u\) 为偶数，则令 \(u=2v,u+1=2v+1\)，发现 \(f(u)\) 会递归到 \(f(v)\)，\(f(u+1)\) 会递归到 \(f(v)\) 和 \(f(v+1)\)。然后两个 \(f(v)\) 就会“合并”，于是可以认为 \(f(u)\) 的计算被 \(f(u+1)\) 吞掉了，也就是等价于只递归到 \(f(u+1)\)。于是这时候 \(n\) 也会减半。

综上所述，计算复杂度为 \(O(\log n)\)，是否再带一个 \(\log\) 取决于用 map 还是 multimap。

定理 11：\(n\) 个点 \(k\) 个大小分别为 \(a_1,\dots,a_k\) 的若干连通块，其形成生成树个数为 \(n^{k-2}\prod a_i\)。

证明：

答案即为

\[\sum\limits_{\{d_i\}}=\binom{k-2}{d_1-1,d_2-1,\dots,d_k-1}\prod\limits_{i=1}^k a_i^{d_i}
\]

（设第 \(i\) 个连通块的度数为 \(d_i\)，则其在 Prufer 序列中出现 \(d_i-1\) 次）

令 \(e_i=d_i-1\)，得到

\[\prod a_i \sum\limits_{\{e_i\}}=\binom{k-2}{e_1,e_2,\dots,e_k}\prod\limits_{i=1}^k a_i^{e_i}
\]

而我们发现由广义二项式定理得：

\[(s_1+s_2+\dots+s_k)^t=\prod\limits_{c_1+c_2+\dots+c_k=t} \binom{t}{c_1,c_2,\dots,c_k}\prod s_i^{c_i}
\]

且 \(e_1+e_2+\dots+e_k=n-2\)，于是一步转化：

\[(a_1+a_2+\dots+a_k)^{k-2}\prod a_i=n^{k-2}\prod a_i
\]

定理 12：当将一棵树上所有点按 bfs 序排序时，一个点前面所有与其距离不超过 \(k\) 的点两两距离不超过 \(k\)。

证明： 由 bfs 序的最短距离性不难验证。

定理 13：\(\sum\limits_{k=2}^n \sqrt \frac{n}{k}=O(n)\)。

证明：

\[\begin{aligned}
& \sum\limits_{k=2}^n \sqrt \frac{n}{k}\\
= & \int_{x=2}^n \sqrt \frac{n}{x} dx\\
= & \sqrt{n} \int_{x=2}^n x^{-1/2} dx\\
= & \sqrt{n} [2x^{1/2}]_{x=2}^n \\
= & \sqrt{n} (2\sqrt n-2\sqrt 2) = O(n)
\end{aligned}
\]

定理 14：一个长为 \(n\) 的串本质不同的回文子串个数为 \(O(n)\)。

证明：

由马拉车算法易得，或者发现以每个右端点结尾的回文串本质不同的都只有至多一个，否则反射到左边会有一个相同的。

定理 15：网络流增广次数至多为 \(O(maxflow)\) 次。

证明：

由于每次增广至少会使流量 +1，这是显然的。注意在大部分建出来的图中，这个上界就是 \(O(n)\) 的。

定理 16：一个单位向量 \((1,0)\) 在 \([0\pi)\) 中随机角度的直线上的投影期望长度为 \(\frac 2 \pi\approx 0.636\)。

证明：

只需要考虑 \(\theta \in [0,\frac \pi 2)\) 的部分。

\[\frac{\int_{\theta=0}^{\frac \pi 2} cos\theta}{\pi/2} = \frac{[sin\theta]_{\theta=0}^{\frac \pi 2}}{\pi/2}=\frac 2 \pi\approx 0.636
\]

定理 17.1：\([m\subseteq n]=\binom{n}{m}\bmod 2\)。

证明：

由 Lucas 定理易证！

定理 17.2：\(\Big(\sum\limits_{\sum x_i=s} \prod [x_i\subseteq a_i]\Big )\bmod 2=\sum\limits_{\sum x_i=s} \prod \binom{a_i}{x_i}\bmod 2=\binom{\sum a_i}{s}\bmod 2\)

证明：

由定理 17.1 与范德蒙德卷积易证。实在是定理 17.1 的一种极其巧妙的用法！！

定理 18.1：对于一张图，令 \(f(S)\) 表示 \(S\) 中的点与 \(S\) 外的点的连边数量，则 \(f(AB)+f(BC)\ge f(A)+f(C)\)

证明：

\[f(AB)=AC+AD+BC+BD\\
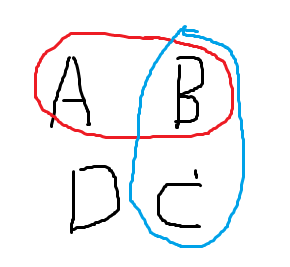
f(BC)=AB+AC+BD+CD\\
f(A)=AB+AC+AD\\
f(C)=AC+BC+CD\\
f(AB)+f(BC)=f(A)+f(C)+2BD
\]

定理 18.2：对于一张图，令 \(f(S)\) 表示 \(S\) 中的点与 \(S\) 外的点的连边数量，则 \(f(AB)+f(BC)\ge f(ABC)+f(B)\)

证明：

\[f(AB)=AC+AD+BC+BD\\
f(BC)=AB+AC+BD+CD\\
f(ABC)=AD+BD+CD\\
f(B)=AB+BC+BD\\
f(AB)+f(BC)=f(ABC)+f(B)+2AC
\]

结论 18.3：\(f(ABC)-f(AB)\le f(BC)-f(B)\)，可以认为由于 \(AB\ge B\)，所以 \(C\) 的影响较小，这种性质称之为“次模性”。

定理 19：\(F_{n+1}=\sum\limits_i \binom{n-i}{i}\)，其中 \(F\) 为斐波那契数列。

证明：

考虑 \(F_{n+1}\) 的组合意义，可以认为是现在有 \(n+1\) 个格子，一开始站在第一个格子，每次向右跳一格或两格，跳到第 \(n+1\) 个格子的方案数。等式右边的 \(i\) 可以视为枚举“大跳”跳了 \(i\) 次，那么就是现在有 \(n-i\) 步“小跳”，要在其中选出 \(i\) 步插入一格变成“大跳”，方案数为 \(\binom{n-i}{i}\)，于是 \(F_{n+1}=\sum\limits_i \binom{n-i}{i}\)。

定理 20：任意一个 \(2n\) 阶完全图均可以划分为 \(2n-1\) 个完美匹配。

证明：

构造性证明，中间拎出一个点，枚举一个点 \(i\) 和中间点连边，其余边依次为 \((i-1,i+1),(i-2,i+2),\dots\)。博客园动图链接

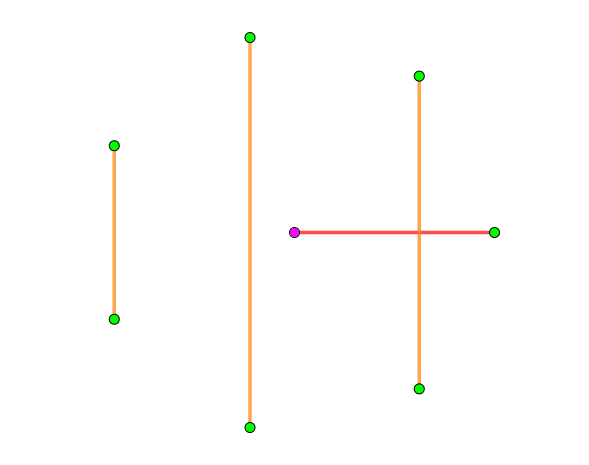
定理 21：\(\max(x,y)=(|x-y|+x+y)/2\le |x-y|/2+|x+y|/2\)！

定理 22：对于一个序列 \(a\) 的任意两种划分方式 \(\delta_1\) 和 \(\delta_2\) 满足 \(|\delta_1|\ge |\delta_2|\)，必然存在 \(\delta_2\) 中的一段是 \(\delta_1\) 中一段的子段。

定理 23：一个图 \(G\) 的任意导出子图中存在一个点的度数 \(\le k\) \(\implies\) 图 \(G\) 可以被 \(k+1\) 染色。

定理 24：一个排列 \(p\) 的逆序对数和它的逆排列 \(p^{-1}\) 的逆序对数相同。

证明： 将排列 \(p\) 视为一个二元组的集合 \((i,p_i)\)，那么 \(p\) 的逆序对数即为集合中满足 \((x_1-x_2)(y_1-y_2)<0\) 的二元组对 \((x_1,y_1),(x_2,y_2)\) 个数。对 \(p\) 取逆后不过是将所有二元组两维交换而已，这个值显然不变。

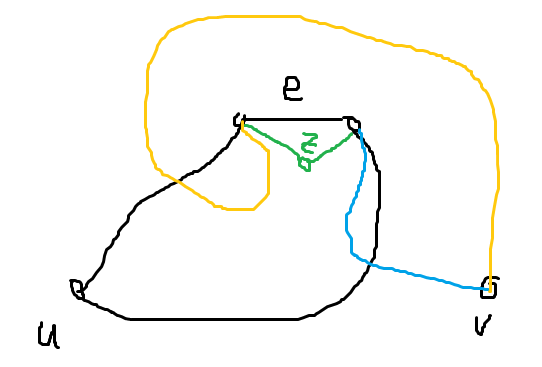
定理 25：对于一个点双连通分量，对于任意两点 \(u,v\) 和一条边 \(e\)，存在 \(u\) 到 \(v\) 的一条简单路径经过边 \(e\)。

证明： 考虑将边 \(e\) 拆除一个点 \(z\) 来，那么显然剩下的图还是一个点双连通分量。

由点双的性质可知，\(u\) 到 \(z\) 存在两条不交的简单路径，\(v\) 到 \(z\) 也存在两条不交的简单路径。注意到 \(z\) 只连出了两条边，于是这两条路径一定是左右两条边各经过一条（绿边）。

考虑 \(v\) 到 \(z\) 的任意一条路径，如果 \(v\) 到 \(z\) 的路径从下方与 \(u\) 到 \(e\) 的路径第一次相交（如蓝边），那 \(u\) 从上方绕路可以过 \(e\)；黄边同理。

证毕。