【Azure 应用服务】FTP 部署 Vue 生成的静态文件至 Linux App Service 后，访问App Service URL依旧显示Azure默认页面问题

问题描述

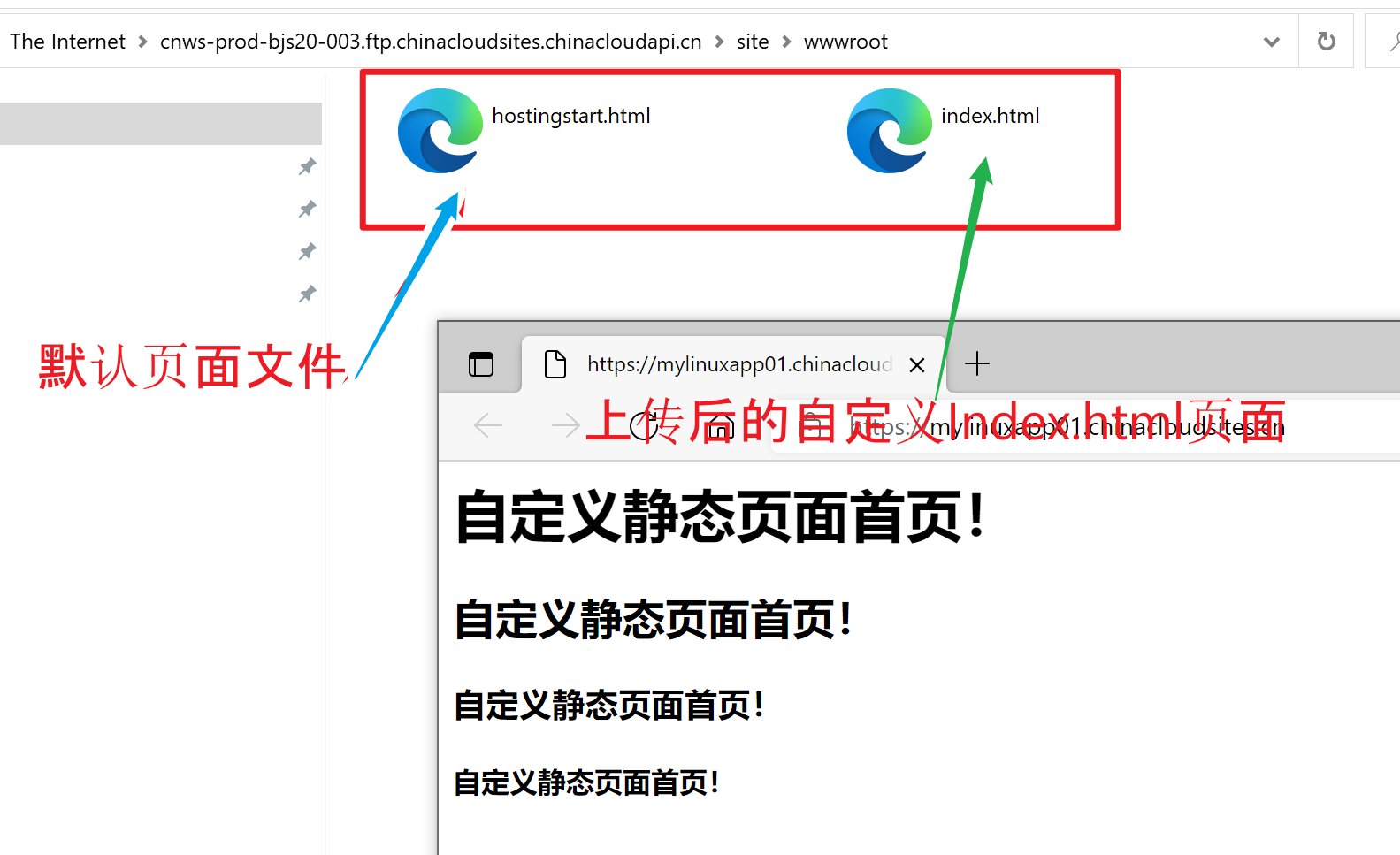
将 JS项目打包为静态文件后，通过 FTP 上传到 App Service For Linux 的 /home/site/wwwroot文件夹中。但打开App Service URL 后依旧显示 Azure 默认页面 (Hey, xxx developers! 欢迎页面)。

是否可以修改默认的启动页面也？类似于在App Service for Windows中的Default Document设置呢？ 如何让index.html文件在Linux中生效作为启动页面？

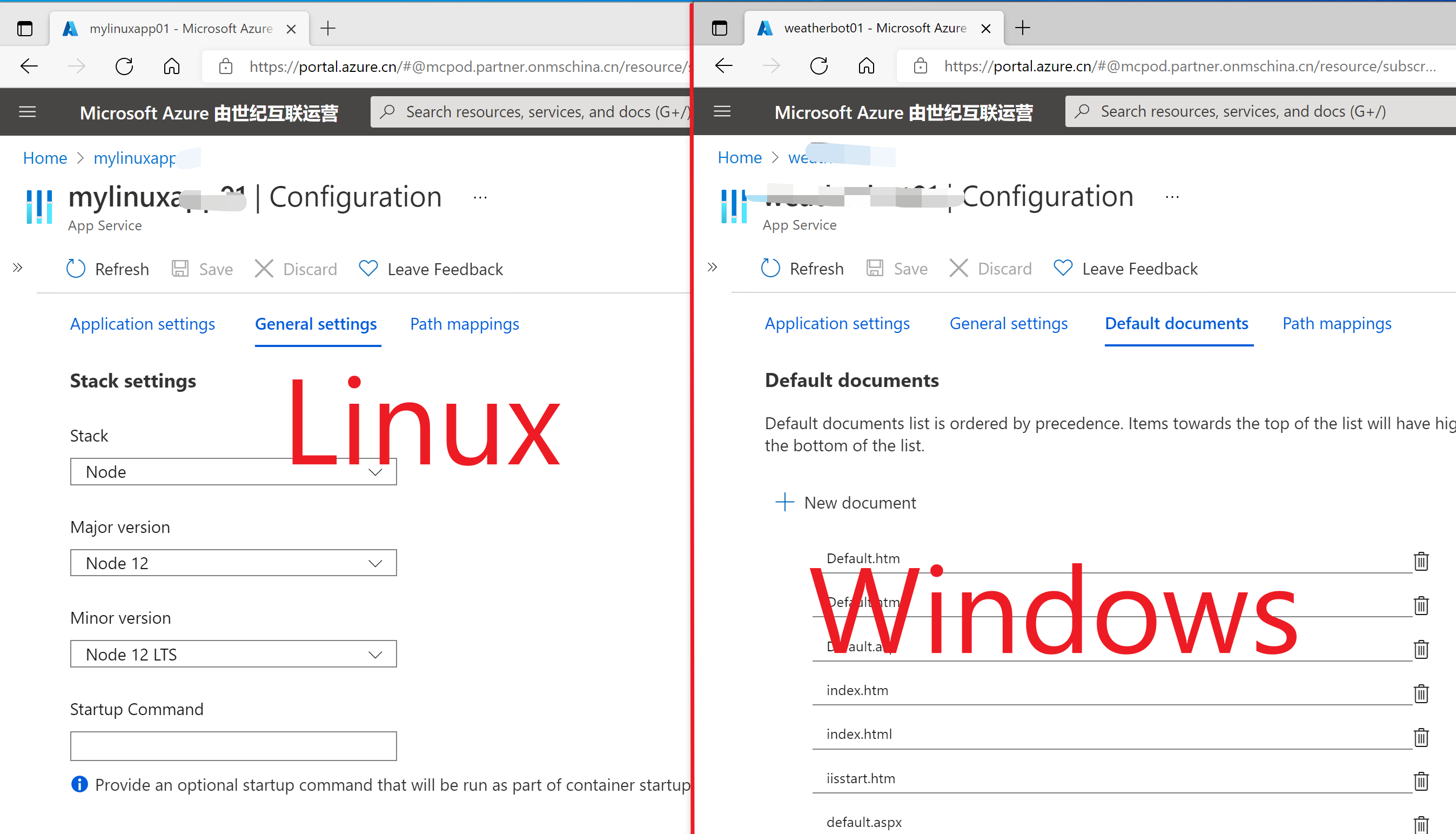
问题解决

在Windows环境中，Default Documents(默认文档)是针对于IIS 服务器而设计的。Linux 环境使用的nginx 服务器这个是没有这个功能的，所以需要通过 Startup Command 进行指定。

操作步骤：

在Linux的Configuration页面的Startup Command中，设置启动命令：pm2 serve /home/site/wwwroot --no-daemon  （PM2 serve: https://pm2.keymetrics.io/docs/usage/expose/）

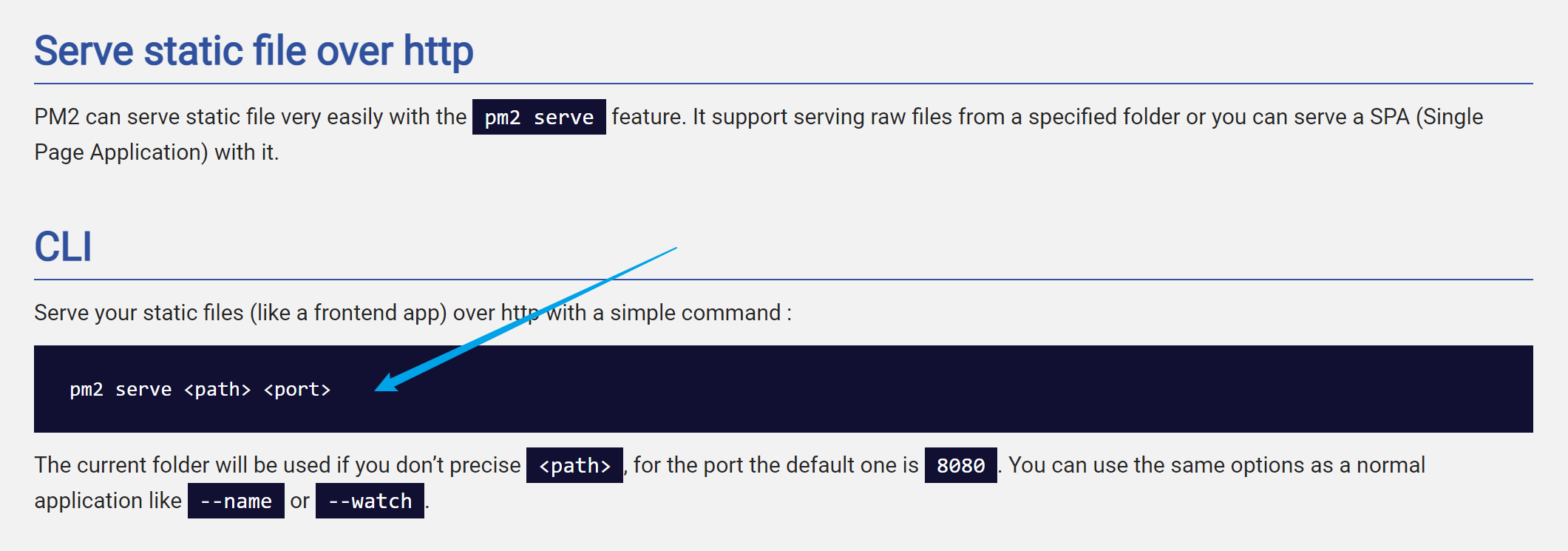
注意：--no-daemon表示让pm2不用守护静态页面的进程，当遇见异常时候不必重启进程。 NodeJS Version 需修改为 12

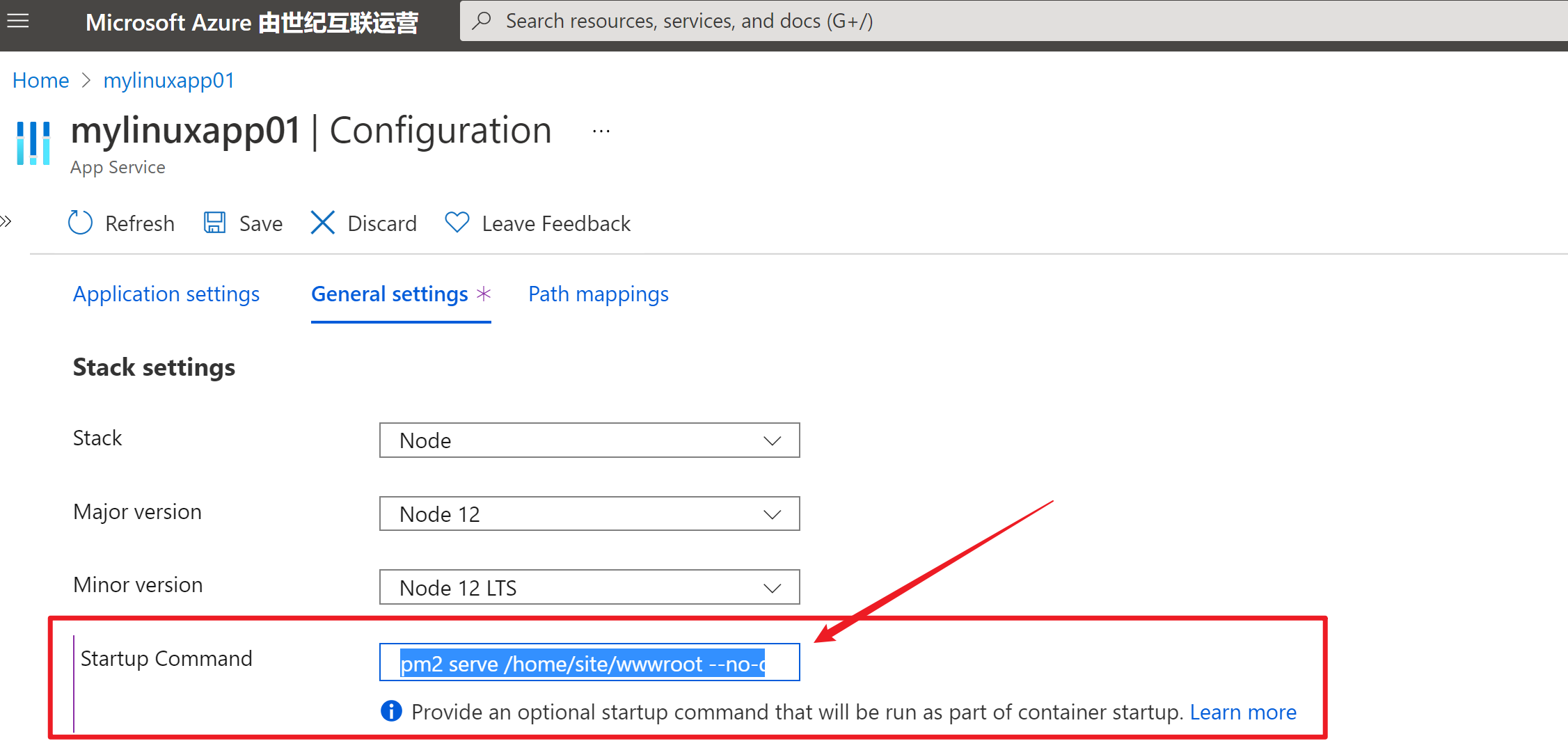
效果展示：

附录一：在Nginx中启用反向代理的简单配置

在Nginx.conf文件中添加如下内容：

server {
        listen       80;
        server_name  www.microsoft.com;

        location / {
            proxy_pass http://127.0.0.1:8080;
            index  index.html;
        }
    }
    

1. listen：表示监听80端口
2. server_name: 表示当访问的服务是www.microsoft.com时
3. location / ：表示是www.microsoft.com下的所有路径请求时，都反向代理到http://127.0.0.18080，访问的首页为index.html。

参考资料

为 Azure 应用服务配置 Node.js 应用：https://docs.azure.cn/zh-cn/app-service/configure-language-nodejs?pivots=platform-linux#run-with-pm2

nginx 反向代理：https://www.cnblogs.com/ysocean/p/9392908.html