2023-07-18：给你一个正整数数组 nums，请你移除 最短 子数组（可以为 空）， 使得剩余元素的 和 能被 p 整除。 不允许 将整个数组都移除。 请你返回你需要移除的最短子数组的长度，如果

2023-07-18：给你一个正整数数组 nums，请你移除 最短 子数组（可以为 空），

使得剩余元素的 和 能被 p 整除。 不允许 将整个数组都移除。

请你返回你需要移除的最短子数组的长度，如果无法满足题目要求，返回 -1 。

子数组 定义为原数组中连续的一组元素。

输入：nums = [3,1,4,2], p = 6。

输出：1。

答案2023-07-18：

大体过程如下：

1.计算整个数组的和对p取余，得到allMod。

2.初始化一个空的映射m，并将映射中键为0，值为-1。该映射用于记录前缀和的某个余数最晚出现的位置。

3.初始化一个变量ans，表示最短子数组的长度，初值为无穷大。

4.初始化一个变量curMod，表示当前的前缀和余数，初值为0。

5.初始化一个变量find，表示要查找的余数，初值为0。

6.遍历数组nums中的每个元素：

• 将当前元素加到curMod中，并对p取余，得到当前前缀和的余数curMod。

• 计算要查找的余数find = (curMod - allMod + p) % p。

• 在映射m中查找余数为find的键，如果存在则计算当前位置与查找到的位置之差，并更新ans为较小的值。

• 更新映射m，将当前余数curMod存储到映射中。

7.如果ans没有被更新，则返回-1，否则返回ans。

代码的时间复杂度为O(n)，其中n是数组nums的长度。这是因为在遍历数组nums的过程中，需要进行常数时间的操作，包括计算前缀和的余数、更新映射m等。

代码的空间复杂度为O(n)，其中n是数组nums的长度。这是因为需要使用一个映射m来记录前缀和的余数及其最晚出现的位置，映射m的大小不会超过数组的长度n。此外，还需要用几个额外的变量来存储一些中间结果，这些变量的空间占用也是常数级别的，不会随着输入规模n的增大而增加。

go完整代码如下：

package main
import (
	"fmt"
)
func minSubarray(nums []int, p int) int {
	n := len(nums)
	// 求出整体的余数
	allMod := 0
	for _, num := range nums {
		allMod = (allMod + num) % p
	}
	if allMod == 0 {
		return 0
	}
	// 记录前缀和的某个余数，最晚出现的位置
	// 看课！然后看接下来的代码
	m := make(map[int]int)
	m[0] = -1
	ans := 1<<31 - 1
	curMod := 0
	var find int
	for i := 0; i < n; i++ {
		// 0...i 累加和的余数
		curMod = (curMod + nums[i]) % p
		// 如果p = 7，整体余数2，当前余数5，那么找之前的部分余数是3
		// 如果p = 7，整体余数2，当前余数1，那么找之前的部分余数是6
		// 整体变成下面的公式，可以自己带入各种情况验证
		find = (curMod - allMod + p) % p
		val, ok := m[find]
		if ok {
			if i != n-1 || val != -1 {
				// 防止删掉整体！
				// ...i(n-1)
				ans = min(ans, i-val)
			}
		}
		m[curMod] = i
	}
	if ans == 1<<31-1 {
		return -1
	}
	return ans
}
func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}
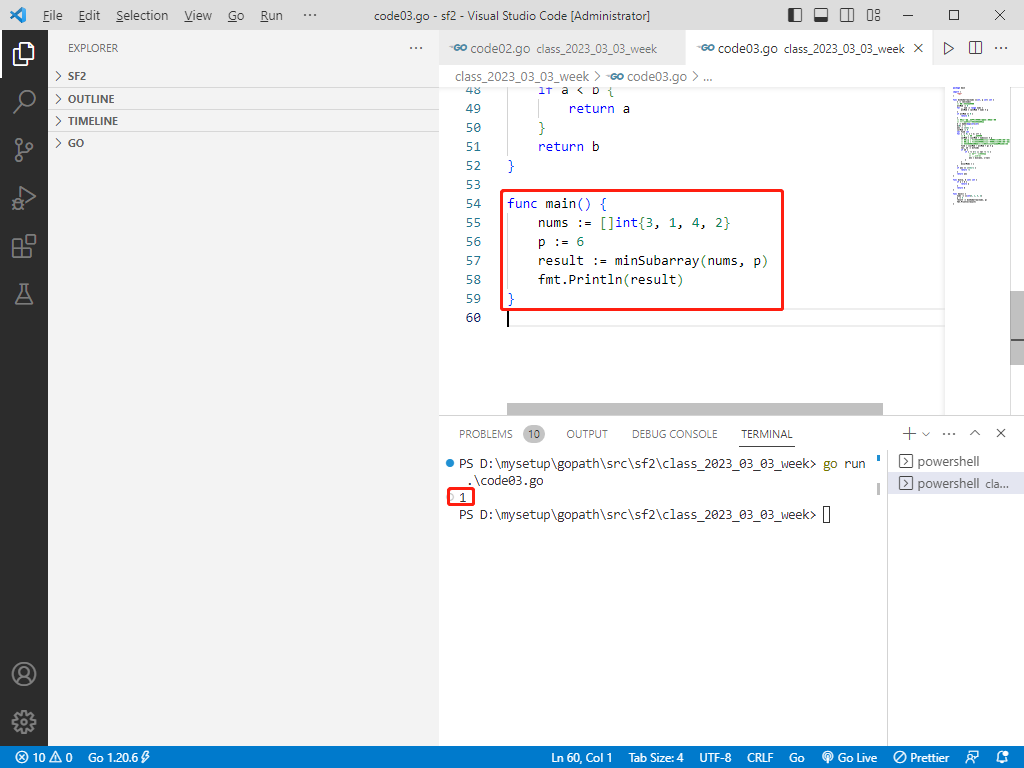
func main() {
	nums := []int{3, 1, 4, 2}
	p := 6
	result := minSubarray(nums, p)
	fmt.Println(result)
}

rust代码如下：

use std::collections::HashMap;
fn min_subarray(nums: Vec<i32>, p: i32) -> i32 {
    let n = nums.len();
    // 求出整体的余数
    let all_mod: i32 = nums.iter().sum::<i32>() % p;
    if all_mod == 0 {
        return 0;
    }
    // 记录前缀和的某个余数，最晚出现的位置
    let mut map: HashMap<i32, i32> = HashMap::new();
    map.insert(0, -1);
    let mut ans = i32::max_value();
    let mut cur_mod = 0;
    let mut find;
    for i in 0..n {
        // 0...i 累加和的余数
        cur_mod = (cur_mod + nums[i]) % p;
        // 如果p = 7，整体余数2，当前余数5，那么找之前的部分余数是3
        // 如果p = 7，整体余数2，当前余数1，那么找之前的部分余数是6
        // 整体变成下面的公式，可以自己带入各种情况验证
        find = (cur_mod - all_mod + p) % p;
        if map.contains_key(&find) {
            if i != n - 1 || map[&find] != -1 {
                // 防止删掉整体！
                // ...i(n-1)
                ans = ans.min(i as i32 - map[&find]);
            }
        }
        map.insert(cur_mod, i as i32);
    }
    return if ans == i32::max_value() { -1 } else { ans };
}
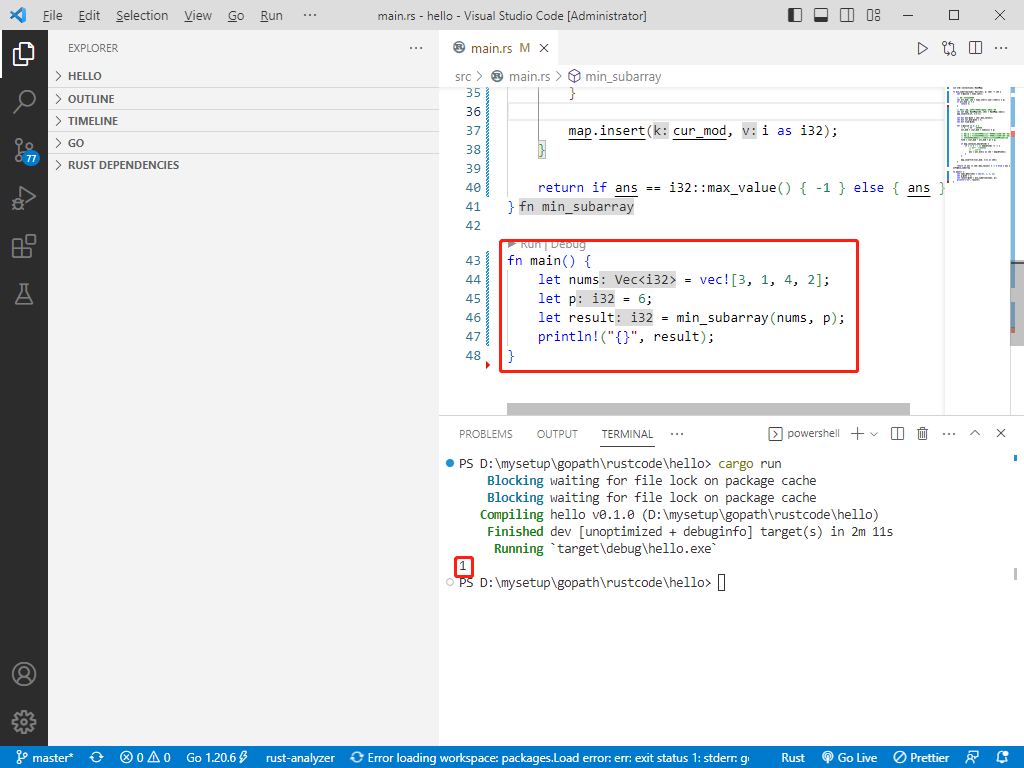
fn main() {
    let nums = vec![3, 1, 4, 2];
    let p = 6;
    let result = min_subarray(nums, p);
    println!("{}", result);
}

c++完整代码如下：

#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
int minSubarray(vector<int>& nums, int p) {
    int n = nums.size();
    // 求出整体的余数
    int allMod = 0;
    for (int num : nums) {
        allMod = (allMod + num) % p;
    }
    if (allMod == 0) {
        return 0;
    }
    // 记录前缀和的某个余数，最晚出现的位置
    // 看课！然后看接下来的代码
    unordered_map<int, int> map;
    map[0] = -1;
    int ans = INT_MAX;
    int curMod = 0, find;
    for (int i = 0; i < n; i++) {
        // 0...i 累加和的余数
        curMod = (curMod + nums[i]) % p;
        // 如果p = 7，整体余数2，当前余数5，那么找之前的部分余数是3
        // 如果p = 7，整体余数2，当前余数1，那么找之前的部分余数是6
        // 整体变成下面的公式，可以自己带入各种情况验证
        find = (curMod - allMod + p) % p;
        if (map.find(find) != map.end()) {
            if (i != n - 1 || map[find] != -1) {
                // 防止删掉整体！
                // ...i(n-1)
                ans = min(ans, i - map[find]);
            }
        }
        map[curMod] = i;
    }
    return (ans == INT_MAX) ? -1 : ans;
}
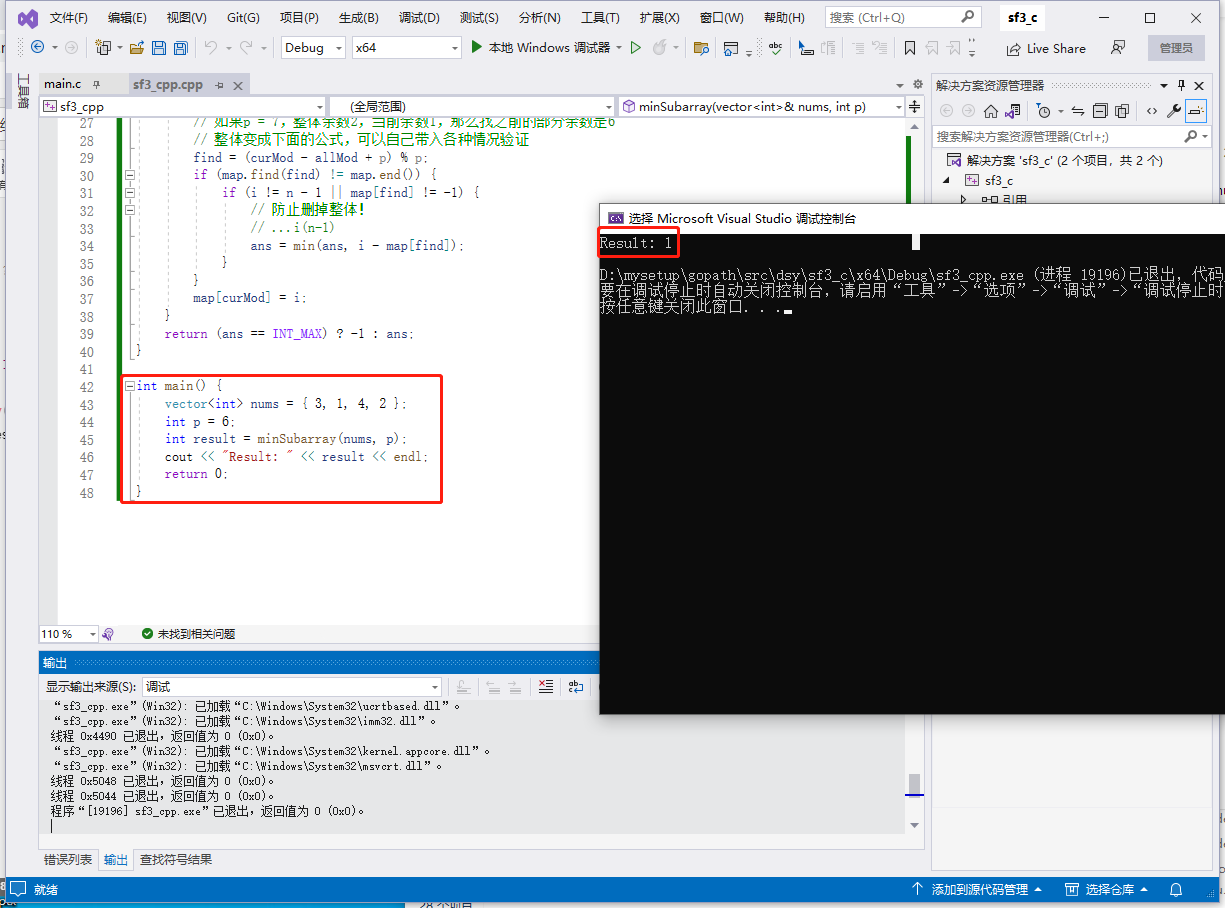
int main() {
    vector<int> nums = { 3, 1, 4, 2 };
    int p = 6;
    int result = minSubarray(nums, p);
    cout << "Result: " << result << endl;
    return 0;
}

c完整代码如下：

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
int minSubarray(int* nums, int numsSize, int p) {
    int n = numsSize;
    // 求出整体的余数
    int allMod = 0;
    for (int i = 0; i < n; i++) {
        allMod = (allMod + nums[i]) % p;
    }
    if (allMod == 0) {
        return 0;
    }
    // 记录前缀和的某个余数，最晚出现的位置
    // 看课！然后看接下来的代码
    int* map = (int*)malloc(sizeof(int) * p);
    for (int i = 0; i < p; i++) {
        map[i] = -1;
    }
    map[0] = -1;
    int ans = INT_MAX;
    int curMod = 0, find;
    for (int i = 0; i < n; i++) {
        // 0...i 累加和的余数
        curMod = (curMod + nums[i]) % p;
        // 如果p = 7，整体余数2，当前余数5，那么找之前的部分余数是3
        // 如果p = 7，整体余数2，当前余数1，那么找之前的部分余数是6
        // 整体变成下面的公式，可以自己带入各种情况验证
        find = (curMod - allMod + p) % p;
        if (map[find] != -1) {
            if (i != n - 1 || map[find] != -1) {
                // 防止删掉整体！
                // ...i(n-1)
                ans = (ans < i - map[find]) ? ans : i - map[find];
            }
        }
        map[curMod] = i;
    }
    free(map);
    return (ans == INT_MAX) ? -1 : ans;
}
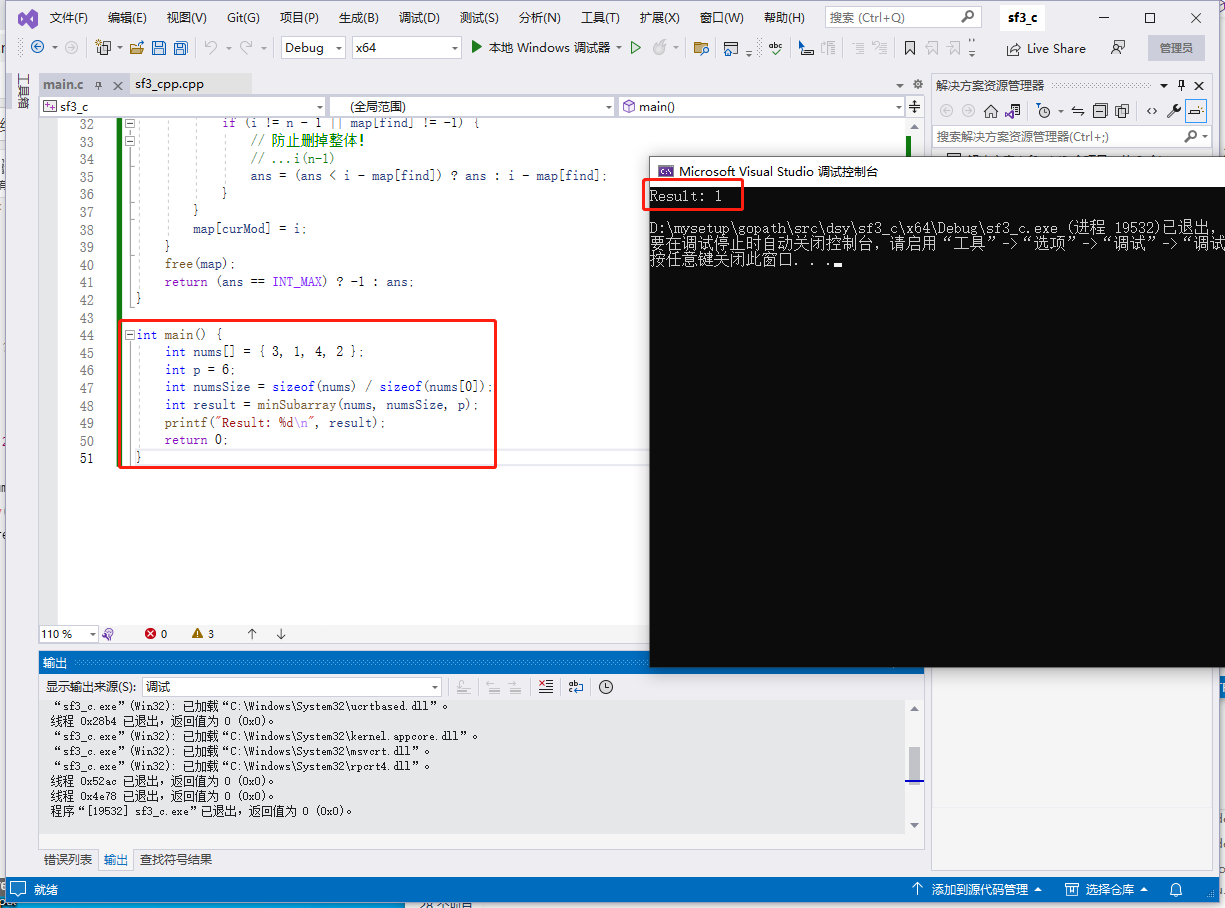
int main() {
    int nums[] = { 3, 1, 4, 2 };
    int p = 6;
    int numsSize = sizeof(nums) / sizeof(nums[0]);
    int result = minSubarray(nums, numsSize, p);
    printf("Result: %d\n", result);
    return 0;
}