TensorFlow 深度学习笔记 从线性分类器到深度神经网络

转载请注明作者：梦里风林
Github工程地址：https://github.com/ahangchen/GDLnotes
欢迎star，有问题可以到Issue区讨论
官方教程地址
视频/字幕下载

Limit of Linear Model

• 实际要调整的参数很多
  

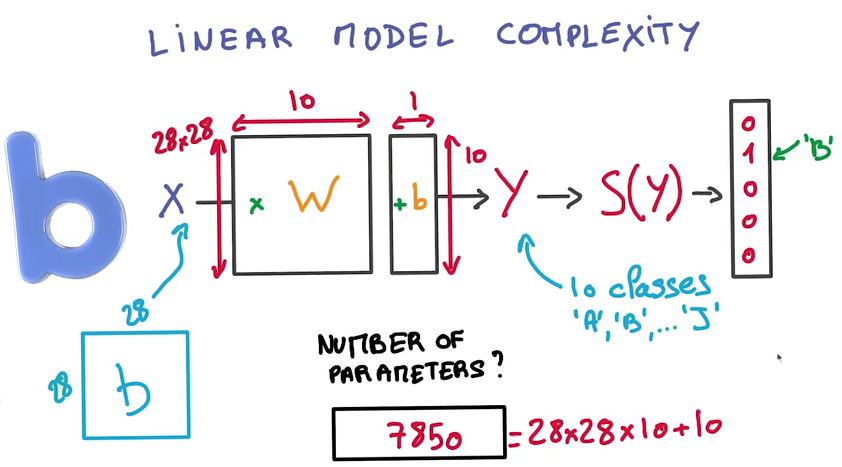
如果有N个Class，K个Label，需要调整的参数就有(N+1)K个

• Linear Model不能应对非线性的问题
  

• Linear Model的好处
• GPU就是设计用于大矩阵相乘的，因此它们用来计算Linear Model非常efficient

• Stable：input的微小改变不会很大地影响output

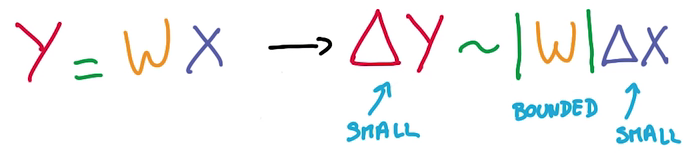
• 求导方便：线性求导是常数

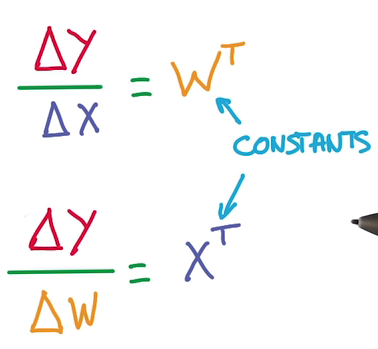
• 我们希望参数函数是线性的，但整个model是非线性的
• 所以需要对各个线性模型做非线性组合
• 最简单的非线性组合：分段线性函数（RELU）

Neural network

• 用一个RELU作为中介，一个Linear Model的输出作为其输入，其输出作为另一个Linear Model的输入，使其能够解决非线性问题

• 神经网络并不一定要完全像神经元那样工作
• Chain Rule：复合函数求导规律

• Lots of data reuse and easy to implement（a simple data pipeline）
• Back propagation

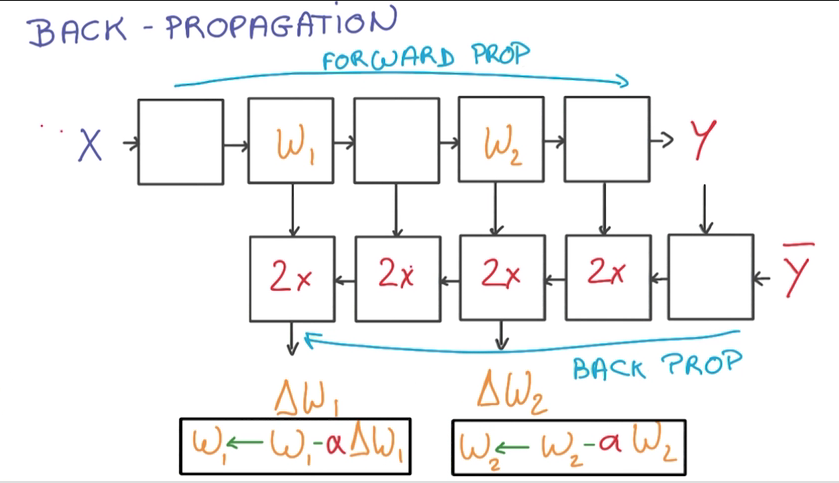
• 计算train_loss时，数据正向流入，计算梯度时，逆向计算
• 计算梯度需要的内存和计算时间是计算train_loss的两倍

Deep Neural Network

Current two layer neural network:

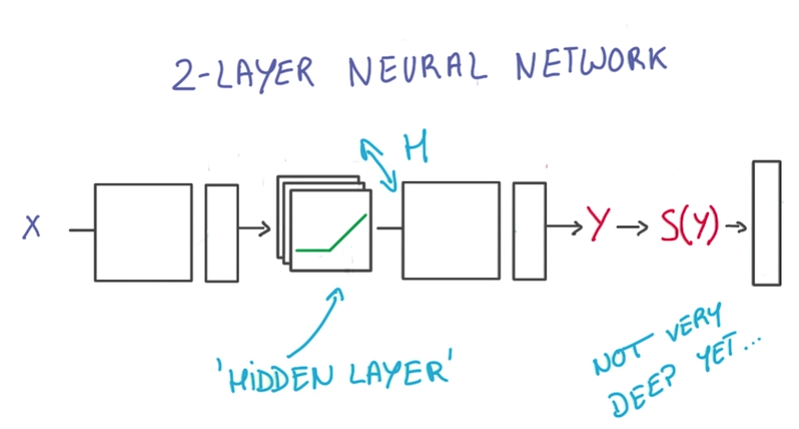
优化：

• 优化RELU(隐藏层), wider

• 增加linear层，layer deeper
  

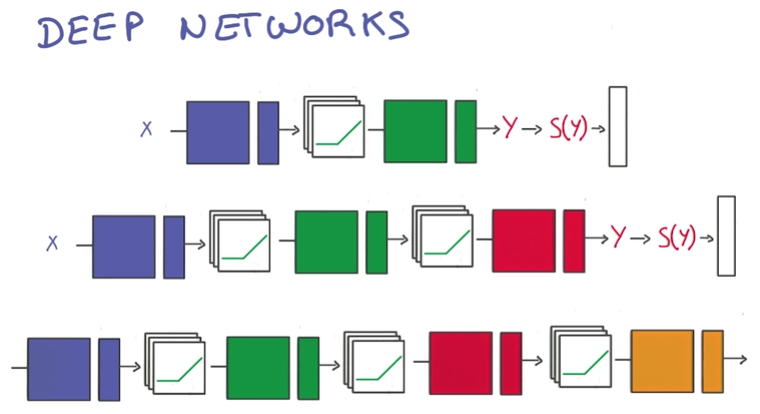
• Performance: few parameters by deeper

• 随层级变高，获得的信息越综合，越符合目标
  

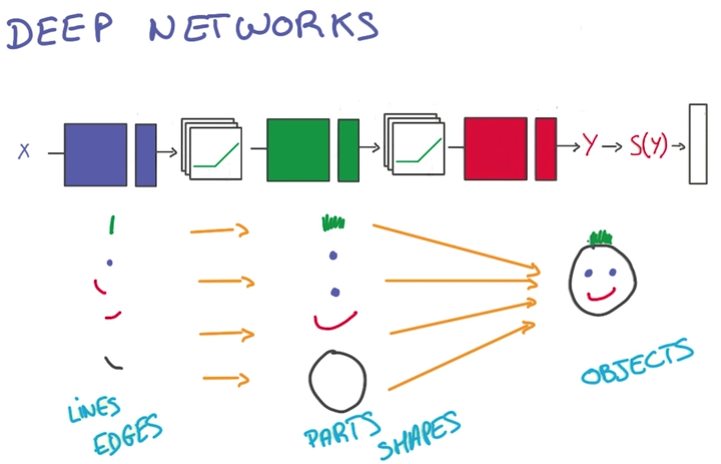
About t-model

• t-model只有在有大量数据时有效
• 今天我们才有高效的大数据训练方法：Better Regularization
• 难以决定适应问题的神经网络的规模，因此通常选择更大的规模，并防止过拟合

Avoid Overfit

Early Termination

• 当训练结果与验证集符合度下降时，就停止训练
  

Regulation

• 给神经网络里加一些常量，做一些限制，减少自由的参数
• L2 regularization

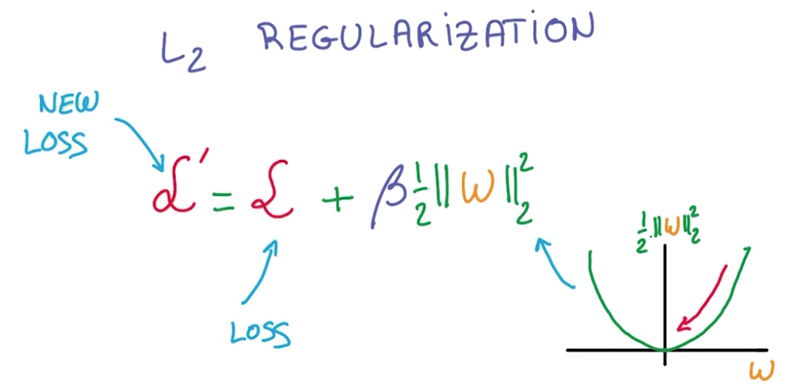
在计算train loss时，增加一个l2 norm作为新的损失，这里需要乘一个β（Hyper parameter），调整这个新的项的值

Hyper parameter：拍脑袋参数→_→

• l2模的导数容易计算，即W本身

  DropOut

  最近才出现，效果极其好

• 从一个layer到另一个layer的value被称为activation
• 将一个layer到另一个layer的value的中，随机地取一半的数据变为0，这其实是将一半的数据直接丢掉
• 由于数据缺失，所以就强迫了神经网络学习redundant的知识，以作为损失部分的补充
• 由于神经网络中总有其他部分作为损失部分的补充，所以最后的结果还是OK的
• More robust and prevent overfit

• 如果这种方法不能生效，那可能就要使用更大的神经网络了

• 评估神经网络时，就不需要DropOut，因为需要确切的结果
• 可以将所有Activation做平均，作为评估的依据

• 因为我们在训练时去掉了一半的随机数据，如果要让得到Activation正确量级的平均值，就需要将没去掉的数据翻倍
  

觉得得我的文章对您有帮助的话，就给个star吧～