协方差cov

摘录wiki如下(红色字体是特别标注的部分)：

http://zh.wikipedia.org/wiki/%E5%8D%8F%E6%96%B9%E5%B7%AE

协方差

协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。

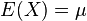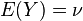期望值分别为与的两个实数随机变量X 与Y 之间的协方差定义为：

，

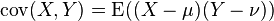其中E是期望值。它也可以表示为：

，

直观上来看，协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

如果X 与Y 是统计独立的，那么二者之间的协方差就是0，这是因为

但是反过来并不成立，即如果X 与Y 的协方差为0，二者并不一定是统计独立的。只能说是线性无关

取决于协方差的相关性η(这东西又叫皮尔逊系数，参见另一篇博文)

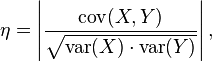=E(XY)/√EX²√EY²

更准确地说是线性相关性，是一个衡量线性独立的无量纲数，其取值在[0,+1]之间。相关性η = 1时称为“完全线性相关”，此时将Y_i对X_i作Y-X 散点图，将得到一组精确排列在直线上的点；相关性数值介于0到1之间时，其越接近1表明线性相关性越好，作散点图得到的点的排布越接近一条直线。

相关性为0（因而协方差也为0）的两个随机变量又被称为是不相关的，或者更准确地说叫作“线性无关”、“线性不相关”，这仅仅表明X 与Y 两随机变量之间没有线性相关性，并非表示它们之间一定没有任何内在的（非线性）函数关系，和前面所说的“X、Y二者并不一定是统计独立的”说法一致。

如果要用公式写一下的话，注意，当X,Y是线性相关的变量时（均去中心化，那么Y和X就是倍数关系），Y=aX。截距b被去中心化了

对η还是要再说明一下：这个东西是衡量X,Y的线性相关程度的。也可以通俗的讲，η衡量的是X，Y的关系有“多像”线性相关。也就是说它是从线性相关的角度来观察X和Y的。如果XY就是线性相关的，那自然η就是1，确实“很像”；但如果XY是其他相关，比如对数相关y=log(x)y之类的，η也是衡量这个对数相关有“多像”线性相关。更深究一点，衡量有“多像”这个事情，实际上是衡量Y与X的变化趋势是否保持一致，比如x扩大几倍，y也扩大几倍。倍数越不一样说明越不像线性相关。

属性

如果X 与Y 是实数随机变量，a 与b 不是随机变量，那么根据协方差的定义可以得到：

，

，

，

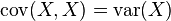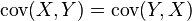对于随机变量序列X₁, ..., X_n与Y₁, ..., Y_m，有

，

对于随机变量序列X₁, ..., X_n，有

。

协方差矩阵[编辑]

分别为m 与n 个标量元素的列向量随机变量X 与Y，二者对应的期望值分别为μ与ν，这两个变量之间的协方差定义为m×n 矩阵

两个向量变量的协方差cov(X, Y)与cov(Y, X)互为转置矩阵。

协方差有时也称为是两个随机变量之间“线性独立性”的度量，但是这个含义与线性代数中严格的线性独立性线性独立不同。