R 《回归分析与线性统计模型》page119,4.2

rm(list = ls())
library(openxlsx)
library(MASS)
data = read.xlsx("xiti_4.xlsx",sheet = 2)
data
fm = lm(y~x1+x2+x3+x4+x5+x6+x7,data)
par(mfrow = c(2,2),mar = 0.4+c(4,4,1,1),oma = c(0,0,2,0))
a1 = boxcox(fm,lambda = seq(0,1,by = 0.1))

　　

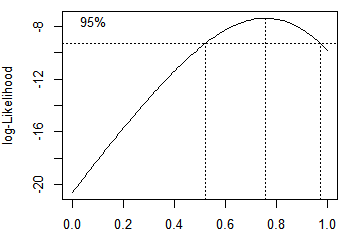
#λ=0.76
l = which(a1$y==max(a1$y))
a1$x[l] #得到0.76就是图像的最高点

　　

lamb = 0.76
ylam = (data$y^lamb -1)/lamb
new_data = cbind(data,ylam)
fm1 = lm(ylam~x1+x2+x3+x4+x5+x6+x7,new_data ) #数据变换后拟合的模型
#计算t外部学生化残差
ei = resid(fm1)
X = cbind(1,as.matrix(data[,2:8]))
t = ti(ei,X)

　　

#残差图
plot(fitted(fm1),t)

　　

从图中看出，没有显示出明显的方差不齐的迹象

#正态性检验
shapiro.test(resid(fm1))

> shapiro.test(resid(fm1))

	Shapiro-Wilk normality test

data:  resid(fm1)
W = 0.97405, p-value = 0.748

　　正态性检验通过

最终的回归模型：