<老古董>1962年的线性支持向量机解法
我们说“训练”支持向量机模型,其实就是确定"最大间隔超平面"。
用数学语言来说就是确定一个最优的W。好比训练一个逻辑回归模型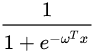 的目的是确定最优的W和b。
的目的是确定最优的W和b。
输入 X,为一个n维向量
输出 y,为-1或1
1.”弱鸡版支持向量机“——硬间隔 线性支持向量机(1962)
我更喜欢叫它 ”弱鸡版支持向量机“,因为它还什么都没有。
判别函数 f(X) = sign( W*X + b )。
我们要根据训练数据集{(X,y)}来计算出最优的参数W和b。
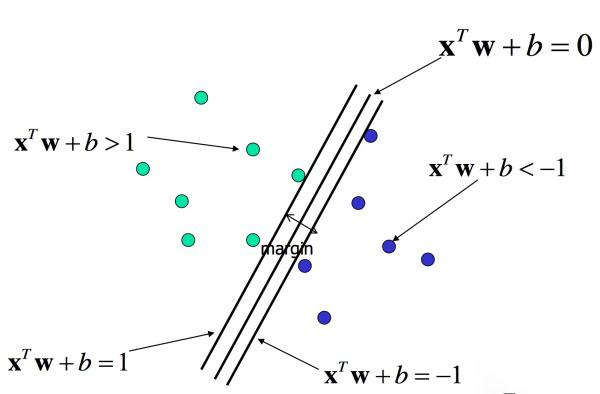
首先基于训练数据集我们有限制条件: y(i) * (W*X(i)+b) >=1,对于训练集中所有的(X(i) ,y(i))。
在此基础上我们找最优的W,也就是使margin = 2 / ||W|| 最大。
总结下来,即求解下面问题,解出最优的W和b。(相比之下,现代神经网络的求解是对于多项式目标函数J(W)求解使J(W)最小的W。只需要使用链式法则和求导计算这两个简单的数学技巧,这应该算是一个明显的进步吧)
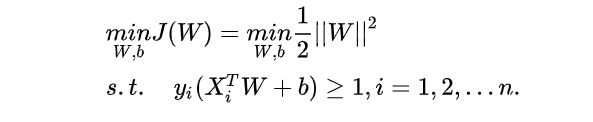
拉格朗日乘子法转换为对偶问题,再KKT条件,
具体数学解决过程这里不写了,较为繁琐。
我们在求解过程中引入了一组拉格朗日乘子,a1,a2,a3,a4.....
推导出:
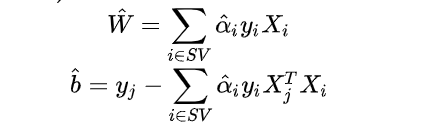
(SV是支持向量们的集合)
解出上式即可。
可以看出,最初支持向量机就是一个完全的数学模型。
2.“勃起版支持向量机”————软间隔 线性支持向量机(1962年)
在前面的硬间隔线性支持向量机上做了一些变化,即给目标函数加了铰链损失项,目标函数变为
J(W) = 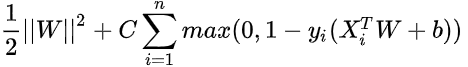
其中称为惩罚参数,
越小时对误分类惩罚越小,越大时对误分类惩罚越大,当
取正无穷时就变成了硬间隔优化。实际应用时我们要合理选取
,
越小越容易欠拟合,
越大越容易过拟合。
(下面用ξ表示铰链函数)
接下来只要采用同样方法求解下面问题即可。
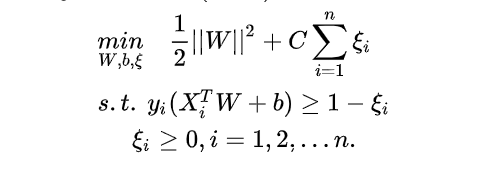
<老古董>1962年的线性支持向量机解法的更多相关文章
- <老古董>线性支持向量机中的硬间隔(hard margin)和软间隔(soft margin)是什么
_________________________________________________________________________________________________ Th ...
- SVM-非线性支持向量机及SMO算法
SVM-非线性支持向量机及SMO算法 如果您想体验更好的阅读:请戳这里littlefish.top 线性不可分情况 线性可分问题的支持向量机学习方法,对线性不可分训练数据是不适用的,为了满足函数间隔大 ...
- 逻辑回归&线性支持向量机
代码: # -*- coding: utf-8 -*- """ Created on Tue Jul 17 10:13:20 2018 @author: zhen &qu ...
- 统计学习:线性支持向量机(SVM)
学习策略 软间隔最大化 上一章我们所定义的"线性可分支持向量机"要求训练数据是线性可分的.然而在实际中,训练数据往往包括异常值(outlier),故而常是线性不可分的.这就要求我们 ...
- 统计学习3:线性支持向量机(Pytorch实现)
学习策略 软间隔最大化 上一章我们所定义的"线性可分支持向量机"要求训练数据是线性可分的.然而在实际中,训练数据往往包括异常值(outlier),故而常是线性不可分的.这就要求我们 ...
- 算法实践——Twitter算法面试题(积水问题)的线性时间解法
问题描述:在下图里我们有不同高度的挡板.这个图片由一个整数数组所代表,数组中每个数是墙的高度.下图可以表示为数组(2.5.1.2.3.4.7.2).假如开始下雨了,那么挡板之间的水坑能够装多少水(水足 ...
- SVM(三)线性支持向量机
本文是在微信公众号发表的原创~ 额,图片粘不过来~就把链接给你们吧 http://mp.weixin.qq.com/s?__biz=MjM5MzM5NDAzMg==&mid=400740076 ...
- 线性可分支持向量机与软间隔最大化--SVM(2)
线性可分支持向量机与软间隔最大化--SVM 给定线性可分的数据集 假设输入空间(特征向量)为,输出空间为. 输入 表示实例的特征向量,对应于输入空间的点: 输出 表示示例的类别. 我们说可以通过间隔最 ...
- 支持向量机原理(四)SMO算法原理
支持向量机原理(一) 线性支持向量机 支持向量机原理(二) 线性支持向量机的软间隔最大化模型 支持向量机原理(三)线性不可分支持向量机与核函数 支持向量机原理(四)SMO算法原理 支持向量机原理(五) ...
随机推荐
- 「Luogu1901」发射站
传送门 Luogu 解题思路 单调栈裸题,扫两遍处理出每个点左边第一个比他高的和右边第一个比他高的,然后模拟题意即可. 细节注意事项 咕咕咕. 参考代码 #include <algorithm& ...
- hdu 1874 畅通工程续(SPFA模板)
畅通工程续 Time Limit: 3000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submi ...
- Python3 中 的 绝对导入 与 相对导入
背景: 在学习tf的时候,看到了from __future__ import absolute_import,所以登记学习一下. 概览: 一般模块导入规则: import xxx时搜索文件的优先级如下 ...
- activity标题栏和状态栏操作
修改显示的标题 1.修改AndroidMainfest.xml文件的label标签 2.setTitle("标签"); 去掉标签的显示 1.android:theme=" ...
- mysq8设置编码utf8
设置mysql默认编码utf8 以及其他配置 系统:centos7 vi /etc/my.cnf #红色部分如果以存在则在他的下方添加 [mysql] default-character-set=ut ...
- Java笔记--网络编程
1.IP地址:InetAddress类 --唯一的标识Internet上的计算机 --本地回环地址(hostAddress)127.0.0.1 主机名(hostName):localhost //根据 ...
- [Codeforces #608 div2]1272B Blocks
Description There are nnn blocks arranged in a row and numbered from left to right, starting from on ...
- /etc/fstab 只读无法修改的解决办法
在做saltstack的时候不小心误把/etc/fstab给注释了 在命令补全的时候开始报错:[root@kafka2 ~]# cat /et-bash: cannot create temp fil ...
- 手把手教你如何玩转CLion
声明:配置是基于CLion的2019.1版本 〇.CLion简介 一.安装 \(JetBrains\)官方下载地址:CLion2019.3 百度网盘:CLion2019.1 个人觉得还是2019.1版 ...
- 13.在项目中部署redis企业级数据备份方案以及各种踩坑的数据恢复容灾演练
到这里为止,其实还是停留在简单学习知识的程度,学会了redis的持久化的原理和操作,但是在企业中,持久化到底是怎么去用得呢? 企业级的数据备份和各种灾难下的数据恢复,是怎么做得呢? 1.企业级的持久化 ...
