Java实现 LeetCode 235 二叉搜索树的最近公共祖先

235. 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

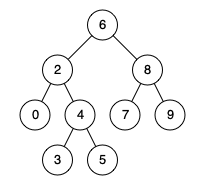
示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8

输出: 6

解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4

输出: 2

解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。

p、q 为不同节点且均存在于给定的二叉搜索树中。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
     TreeNode res = null;
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

        lca(root, p , q);
        return res;
    }

    public void lca(TreeNode root, TreeNode p , TreeNode q){
        if((root.val - p.val)*(root.val - q.val) <= 0){
            res = root;
        }else if(root.val < p.val && root.val < q.val){
            lca(root.right, p , q);
        }else{
            lca(root.left, p , q);
        }
    }
}