【转】动态规划之最长公共子序列（LCS）

【原文链接】最长公共子序列（Longest Common Subsequence，简称 LCS）是一道非常经典的面试题目，因为它的解法是典型的二维动态规划，大部分比较困难的字符串问题都和这个问题一个套路，比如说编辑距离。而且，这个算法稍加改造就可以用于解决其他问题，所以说 LCS 算法是值得掌握的。

题目就是让我们求两个字符串的 LCS 长度：

输入: str1 = "abcde", str2 = "ace"
输出: 3
解释: 最长公共子序列是 "ace"，它的长度是 3

肯定有读者会问，为啥这个问题就是动态规划来解决呢？因为子序列类型的问题，穷举出所有可能的结果都不容易，而动态规划算法做的就是穷举 + 剪枝，它俩天生一对儿。所以可以说只要涉及子序列问题，十有八九都需要动态规划来解决，往这方面考虑就对了。

下面就来手把手分析一下，这道题目如何用动态规划技巧解决。

动态规划思路

第一步，一定要明确 dp 数组的含义。对于两个字符串的动态规划问题，套路是通用的。

比如说对于字符串 s1 和 s2，一般来说都要构造一个这样的 DP table：

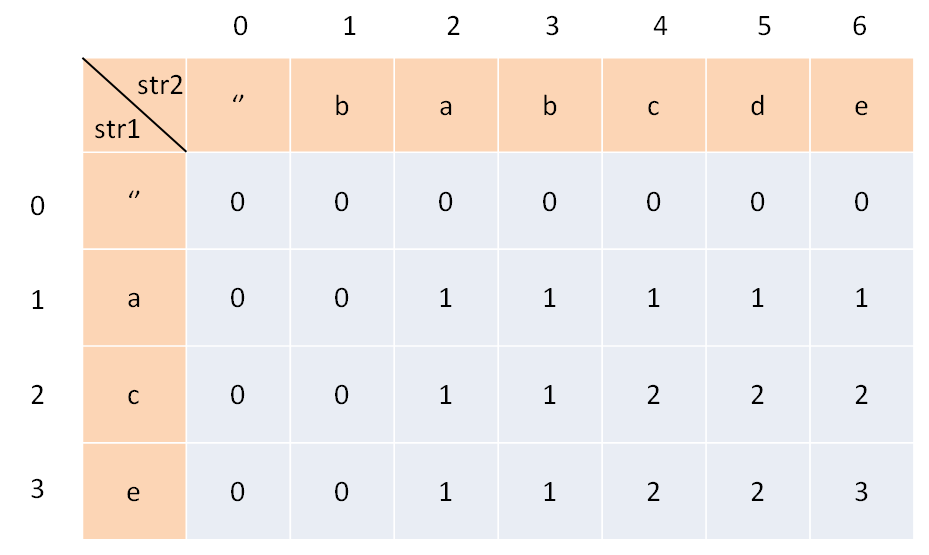
为了方便理解此表，我们暂时认为索引是从 1 开始的，待会的代码中只要稍作调整即可。其中，dp[i][j] 的含义是：对于 s1[1..i] 和 s2[1..j]，它们的 LCS 长度是 dp[i][j]。

比如上图的例子，d[2][4] 的含义就是：对于 "ac" 和 "babc"，它们的 LCS 长度是 2。我们最终想得到的答案应该是 dp[3][6]。

第二步，定义 base case。

我们专门让索引为 0 的行和列表示空串，dp[0][..] 和 dp[..][0] 都应该初始化为 0，这就是 base case。

比如说，按照刚才 dp 数组的定义，dp[0][3]=0 的含义是：对于字符串 "" 和 "bab"，其 LCS 的长度为 0。因为有一个字符串是空串，它们的最长公共子序列的长度显然应该是 0。

第三步，找状态转移方程。

这是动态规划最难的一步，不过好在这种字符串问题的套路都差不多，权且借这道题来聊聊处理这类问题的思路。

状态转移说简单些就是做选择，比如说这个问题，是求 s1 和 s2 的最长公共子序列，不妨称这个子序列为 lcs。那么对于 s1 和 s2 中的每个字符，有什么选择？很简单，两种选择，要么在 lcs 中，要么不在。

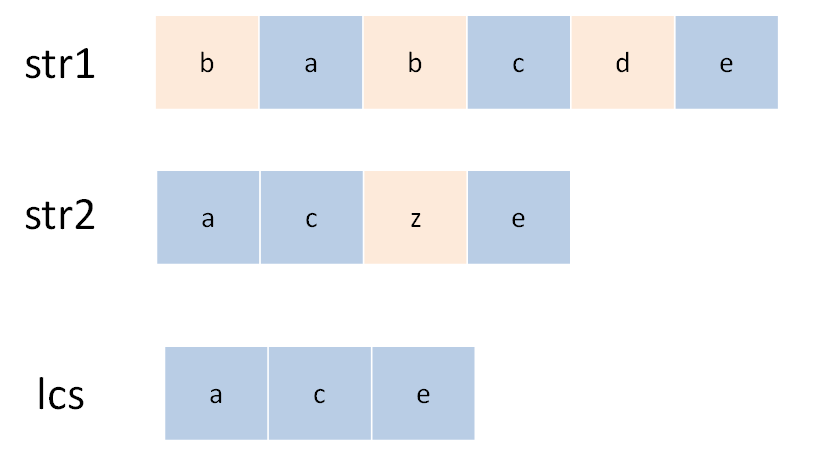
这个「在」和「不在」就是选择，关键是，应该如何选择呢？这个需要动点脑筋：如果某个字符应该在 lcs 中，那么这个字符肯定同时存在于 s1 和 s2 中，因为 lcs 是最长公共子序列嘛。所以本题的思路是这样：

用两个指针 i 和 j 从后往前遍历 s1 和 s2，如果 s1[i]==s2[j]，那么这个字符一定在 lcs 中；否则的话，s1[i] 和 s2[j] 这两个字符至少有一个不在 lcs 中，需要丢弃一个。先看一下递归解法，比较容易理解：

def longestCommonSubsequence(str1, str2) -> int:
    def dp(i, j):
        # 空串的 base case
        if i == -1 or j == -1:
            return 0
        if str1[i] == str2[j]:
            # 这边找到一个 lcs 的元素，继续往前找
            return dp(i - 1, j - 1) + 1
        else:
            # 谁能让 lcs 最长，就听谁的
            return max(dp(i-1, j), dp(i, j-1))

    # i 和 j 初始化为最后一个索引
    return dp(len(str1)-1, len(str2)-1)

对于第一种情况，找到一个 lcs 中的字符，同时将 i j 向前移动一位，并给 lcs 的长度加一；对于后者，则尝试两种情况，取更大的结果。

其实这段代码就是暴力解法，我们可以通过备忘录或者 DP table 来优化时间复杂度，比如通过前文描述的 DP table 来解决：

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int m = text1.length();
        int n = text2.length();
        int[][] dp = new int[m + 1][n + 1];
        for(int i = 1;i <= m;i++){
            for(int j = 1;j <= n;j++){
                if(text1.charAt(i - 1) == text2.charAt(j - 1))
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                else
                    dp[i][j] = Math.max(dp[i - 1][j],dp[i][j - 1]);
            }
        }
        return dp[m][n];
    }
}

总结

对于两个字符串的动态规划问题，一般来说都是像本文一样定义 DP table，因为这样定义有一个好处，就是容易写出状态转移方程，dp[i][j] 的状态可以通过之前的状态推导出来：

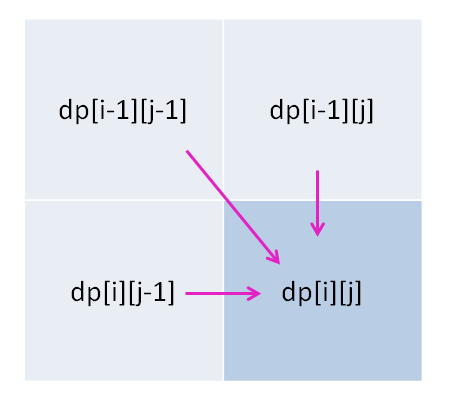
找状态转移方程的方法是，思考每个状态有哪些「选择」，只要我们能用正确的逻辑做出正确的选择，算法就能够正确运行。