3.K均值算法

一、概念

　　K-means中心思想：事先确定常数K，常数K意味着最终的聚类类别数，首先随机选定初始点为质心，并通过计算每一个样本与质心之间的相似度(这里为欧式距离)，将样本点归到最相似的类中，接着，重新计算每个类的质心(即为类中心)，重复这样的过程，直到质心不再改变，最终就确定了每个样本所属的类别以及每个类的质心。由于每次都要计算所有的样本与每一个质心之间的相似度，故在大规模的数据集上，K-Means算法的收敛速度比较慢。

二、特点：

常用距离

a.欧式距离

b.曼哈顿距离

三、算法流程

K-means是一个反复迭代的过程，算法分为四个步骤：

（x,k,y)

（1） 选取数据空间中的K个对象作为初始中心，每个对象代表一个聚类中心；

　　  　　def initcenter(x, k): kc

（2） 对于样本中的数据对象，根据它们与这些聚类中心的欧氏距离，按距离最近的准则将它们分到距离它们最近的聚类中心（最相似）所对应的类；

　　 　　def nearest(kc, x[i]): j

　　　　def xclassify(x, y, kc):y[i]=j

（3） 更新聚类中心：将每个类别中所有对象所对应的均值作为该类别的聚类中心，计算目标函数的值；

　　　　def kcmean(x, y, kc, k):

（4） 判断聚类中心和目标函数的值是否发生改变，若不变，则输出结果，若改变，则返回2）。

　　　　 while flag:

　　　　y = xclassify(x, y, kc)

　　　　kc, flag = kcmean(x, y, kc, k)

四、实践

（1）.扑克牌手动演练k均值聚类过程：>30张牌，3类

①本次模拟k均值用到的扑克牌，初始中心为(2,9,12)

②经过一轮计算（选出中心：3,8,12）

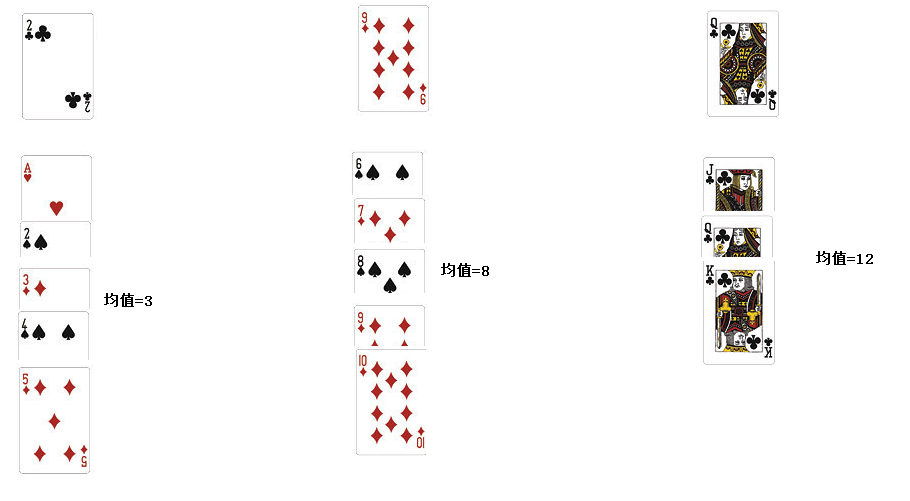
③一直算到最后

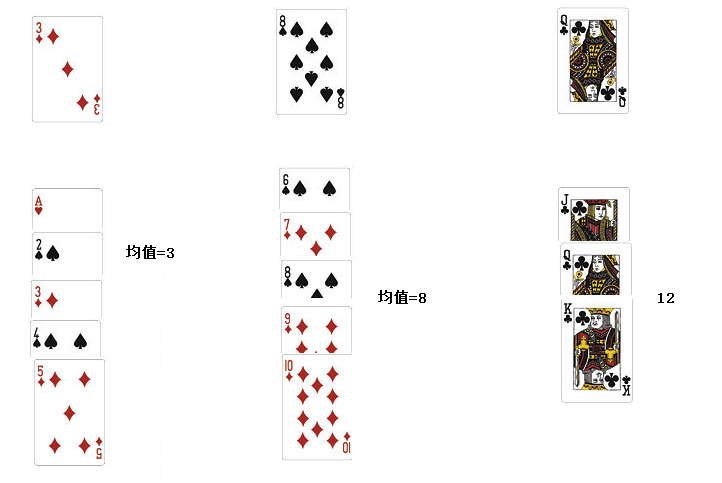
（2）.*自主编写K-means算法 ，以鸢尾花花瓣长度数据做聚类，并用散点图显示。

### 1、导入鸢尾花数据
from sklearn.datasets import load_iris
import numpy as np

### 2、鸢尾花数据
iris = load_iris()
data=iris['data']

#样本属性个数
m=data.shape[1]
#样本个数
n=len(data)
#类中心个数，即最终分类
k=3

### 3、数据初始化
#距离矩阵
dist=np.zeros([n,k+1])
#初始类中心
center=np.zeros([k,m])
#新的类中心
new_center=np.zeros([k,m])
### 4、选中心
#选择前三个样本作为初始类中心
center=data[:k, :]

while True:
    #求距离
    for i in range(n):
        for j in range(k):
            dist[i,j]=np.sqrt(sum((data[i,:]-center[j,:])**2))
        #归类
        dist[i,k]=np.argmin(dist[i,:k])
    #求新类中心
    for i in range(k):
        index=dist[:,k]==i
        new_center[i,:]=np.mean(data[index, :])
    #判断结束
    if(np.all(center==new_center)):
        break
    else:
        center=new_center
print('聚类结果：',dist[:,k])

　　

（3）用sklearn.cluster.KMeans，鸢尾花花瓣长度数据做聚类，并用散点图显示。

from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 获取鸢尾花数据集
iris = load_iris()
data = iris.data[:, 1]
# 鸢尾特征值
x = data.reshape(-1, 1)
# 构建模型
model = KMeans(n_clusters=3)
# 训练
model.fit(x)
# 预测样本的聚类索引
y = model.predict(x)
print("预测结果：", y)
#画图
plt.scatter(x[:, 0], x[:, 0], c=y, s=50, cmap='rainbow')
plt.show()

预测结果：

散点图可视化：

（4）鸢尾花完整数据做聚类并用散点图显示。

from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 导入鸢尾花数据集
iris = load_iris()
# 鸢尾花花瓣长度数据
x = iris.data
# 构建模型
model = KMeans(n_clusters=3)
# 训练
model.fit(x)
# 预测
y = model.predict(x)
print("预测结果：", y)
#画图
plt.scatter(x[:, 2], x[:, 3], c=y, s=50, cmap='rainbow')
plt.show()

　预测结果：

散点图可视化：

（5）想想k均值算法中以用来做什么？

• 文本分析和归类
• K均值算法实现图像压缩
• 像素处理
• K均值算法处理图像