Android实例-解决启动黑屏问题(XE8+小米2)

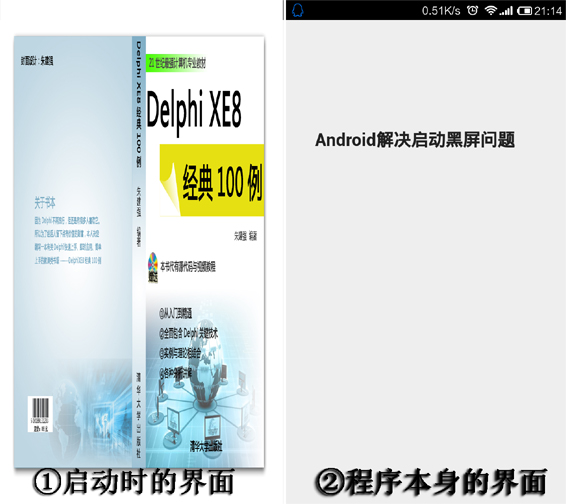
结果：

1.在启动时马上出现图片界面，但在出现程序界面前会有黑屏，大约有0.2秒左右。

实现：

1.建立2个文件：loading.png和styles.xml：

①其中loading.png是启动时替代黑屏的图片。

②styles.xml是对背景图片的定义，其内容为：

 <resources>

      <!--
         Base application theme, dependent on API level. This theme is replaced
          by AppBaseTheme from res/values-vXX/styles.xml on newer devices.
      -->
  <style name="MyTheme.NoTitleBar.CustomBackground" parent="@android:Theme.Black">
          <item name="android:windowBackground">@drawable/loading</item>
          <item name="android:windowNoTitle">true</item>
          <item name="android:windowFullscreen">true</item>
          <item name="android:windowContentOverlay">@null</item>
   </style> 

      <style name="AppBaseTheme" parent="android:Theme.Light">
          <!--
             Theme customizations available in newer API levels can go in
              res/values-vXX/styles.xml, while customizations related to
              backward-compatibility can go here.
          -->
      </style>

      <!-- Application theme. -->
      <style name="AppTheme" parent="AppBaseTheme">
          <!-- All customizations that are NOT specific to a particular API-level can go here. -->
      </style>

  </resources>

2.因为在 Java 下大小写是敏感的，在 styles.xml 定义中“loading ”的这个文件名一定要用小写。

3.文件 styles.xml 和 loading.png 最好放在工程文件所在根目录下。反正不要放在根目录的外面，其下子文件夹倒是可以，文件夹用英文，只是建义，不想找麻烦最好用英文。

4.将建立好的2个文件打包到安装文件中：

①Project  ->Deployment->Add Files->选择文件 styles.xml 和 loading.png。

②PlatForm属性都设置为Android。

③RemotePath属性：

styles.xml 的RemotePath为 res\values\

loading.png 的RemotePath为 res\drawable-port\

5.工程缺省配置文件 AndroidManifest.template.xml：

①Ctrl+F9编译工程文件，并生成相关配置文件，打开工程文件所在目录，就可以找到。

②记事本打开AndroidManifest.template.xml文件，查找以下文字：

android:theme="%theme%"

替换为以下文字，注意是替换，不是新增，然后关闭并保存。

android:theme="@style/MyTheme.NoTitleBar.CustomBackground"。

6. 重新编译。