【策略】UVa 1344 - Tian Ji -- The Horse Racing（田忌赛马）

Here is a famous story in Chinese history.

That was about 2300 years ago. General Tian Ji was a high official in the country Qi. He likes to play horse racing with the king and others.

Both of Tian and the king have three horses in different classes, namely, regular, plus, and super. The rule is to have three rounds in a match; each of the horses must be used in one round. The winner of a single round takes two hundred silver dollars from the loser.

Being the most powerful man in the country, the king has so nice horses that in each class his horse is better than Tian's. As a result, each time the king takes six hundred silver dollars from Tian.

Tian Ji was not happy about that, until he met Sun Bin, one of the most famous generals in Chinese history. Using a little trick due to Sun, Tian Ji brought home two hundred silver dollars and such a grace in the next match.

It was a rather simple trick. Using his regular class horse race against the super class from the king, they will certainly lose that round. But then his plus beat the king's regular, and his super beat the king's plus. What a simple trick. And how do you think of Tian Ji, the high ranked official in China?

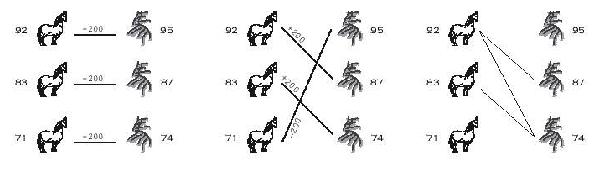
Were Tian Ji lives in nowadays, he will certainly laugh at himself. Even more, were he sitting in the ACM contest right now, he may discover that the horse racing problem can be simply viewed as finding the maximum matching in a bipartite graph. Draw Tian's horses on one side, and the king's horses on the other. Whenever one of Tian's horses can beat one from the king, we draw an edge between them, meaning we wish to establish this pair. Then, the problem of winning as many rounds as possible is just to find the maximum matching in this graph. If there are ties, the problem becomes more complicated, he needs to assign weights 0, 1, or -1 to all the possible edges, and find a maximum weighted perfect matching...

However, the horse racing problem is a very special case of bipartite matching. The graph is decided by the speed of the horses -- a vertex of higher speed always beat a vertex of lower speed. In this case, the weighted bipartite matching algorithm is a too advanced tool to deal with the problem.

In this problem, you are asked to write a program to solve this special case of matching problem.

Input

The input consists of up to 50 test cases. Each case starts with a positive integer n ( n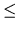1000) on the first line, which is the number of horses on each side. The next n integers on the second line are the speeds of Tian's horses. Then the next n integers on the third line are the speeds of the king's horses. The input ends with a line that has a single `0' after the last test case.

Output

For each input case, output a line containing a single number, which is the maximum money Tian Ji will get, in silver dollars.

Sample Input

3
92 83 71
95 87 74
2
20 20
20 20
2
20 19
22 18
0

Sample Output

200
0
0

贪心策略:

一、当田忌最快的马比国王最快的马快时，用田忌最快的马赢国王最快的马。
二、当田忌最快的马比国王最快的马慢时，用田忌最慢的马输给国王最快的马。
三、当田忌最快的马跟国王最快的马一样快时，分情况。(对于情况三，我们应该从最慢的马开始考虑了)

　　1、当田忌最慢的马比国王最慢的马快，那么用田忌最慢的马赢国王最慢的马

　　2、当田忌最慢的马比国王最慢的马慢，那么用田忌最慢的马输给国王最快的马

　　3、当田忌最慢的马跟国王最慢的马相等的时候，用田忌最慢的马跟国王最快的马比(此时国王最快的马只能大于等于田忌最慢的马，若大于，则田忌输，等于，平局)

 #include<iostream>
 #include<cstdio>
 #include<cstdlib>
 #include<algorithm>
 using namespace std;
 const int maxn = ;
 int t[maxn], k[maxn];
 int main()
 {
     int n;
     while(~scanf("%d", &n) && n)
     {
         for(int i = ; i < n; i++)
         {
             scanf("%d", &t[i]);
         }
         for(int i = ; i < n; i++)
         {
             scanf("%d", &k[i]);
         }
         sort(t, t+n); sort(k, k+n);
         int tmax = n-, kmax = n-; //T和K最快的马的编号
         int tmin = , kmin = ; //T和K最慢的马的编号
         int win = , lose = ;
         while(tmin <= tmax && kmin <= kmax)
         {
             if(t[tmax] > k[kmax])
             {
                 tmax--; kmax--;
                 win++;
             }
             else if(t[tmax] < k[kmax])
             {
                 tmin++; kmax--;
                 lose++;
             }
             else
             {
                 if(t[tmin] > k[kmin])
                 {
                     tmin++; kmin++;
                     win++;
                 }
                 else if(t[tmin] < k[kmin])
                 {
                     tmin++; kmax--;
                     lose++;
                 }
                 else
                 {
                     if(t[tmin] < k[kmax])
                          lose++;
                     tmin++; kmax--;
                 }
             }
         }
         printf("%d\n", ((win-lose)*));
     }
     return ;
 }