20155338 ch02 ch03课下作业

要求：

1、补充完成课上测试（不能只有截图，要有分析，问题解决过程，新学到的知识点）

课上测试-3-ch02

1、编写一个程序 “week0603学号.c",运行下面代码：

（1） short int v = -学号后四位

（2） unsigned short uv = (unsigned short) v

（3） printf("v = %d, uv = %u\n "， v, uv);

2、在第三行设置断点用gdb调试，用p /x v; p /x uv查看变量的值，提交调试结果截图，要全屏，要包含自己的学号信息

3、分析p /x v; p /x uv 与程序运行结果的不同和联系

课上编写完代码，在gdb调试中输入了题目要求的命令，但动作比较慢，没来得及提交上，课后下来上网查了查p/x v 和 p/x uv 之间的联系，也算get到一个知识点。

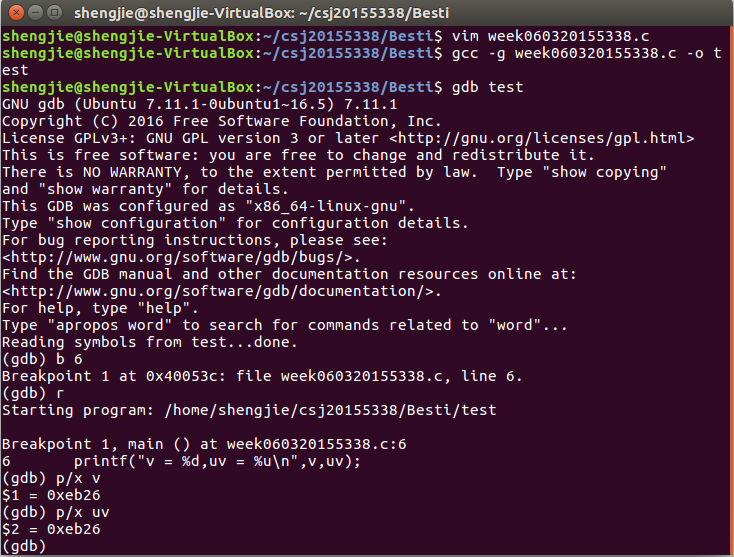
p/x v和 p/x uv之间的联系在于有符号数和无符号数之间的转换，其数值可能会变，但位模式不会变

课上测试-5-ch03

1、通过输入gcc -S -o main.s main.c将下面c程序编译成汇编代码

2、参考博客使用gdb跟踪汇编代码，在纸上画出f中每一条语句引起的eip(rip),ebp(rbp),esp(rsb),eax(rax)的值和栈的变化情况。提交照片，要有学号信息。

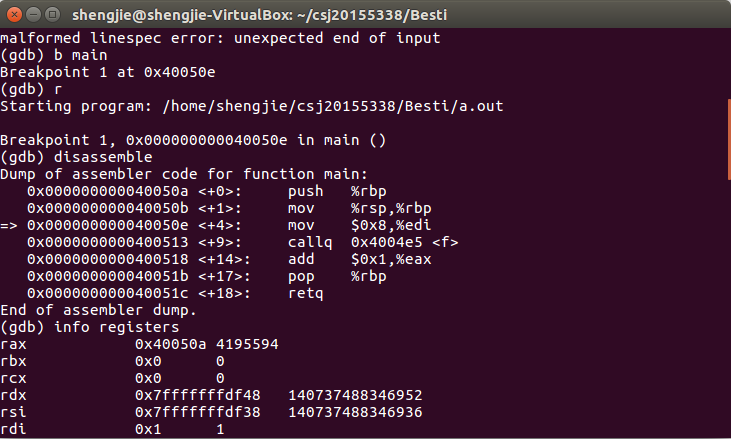
使用disassemble命令获取汇编代码，info registers查看寄存器的值。根据参考博客，ret命令将栈顶弹给%eip，在执行下一条汇编语句之前，设置：display /i $pc，此命令在每次程序中断后可以看到即将被执行的下一条汇编指令，/i表示以十六进制显示，$pc表示当前汇编命令，si执行一条汇编指令。将其变化记录即可。

2、缓冲区溢出漏洞实验

1、输入命令安装一些用于编译32位C程序的东西：

shellcode

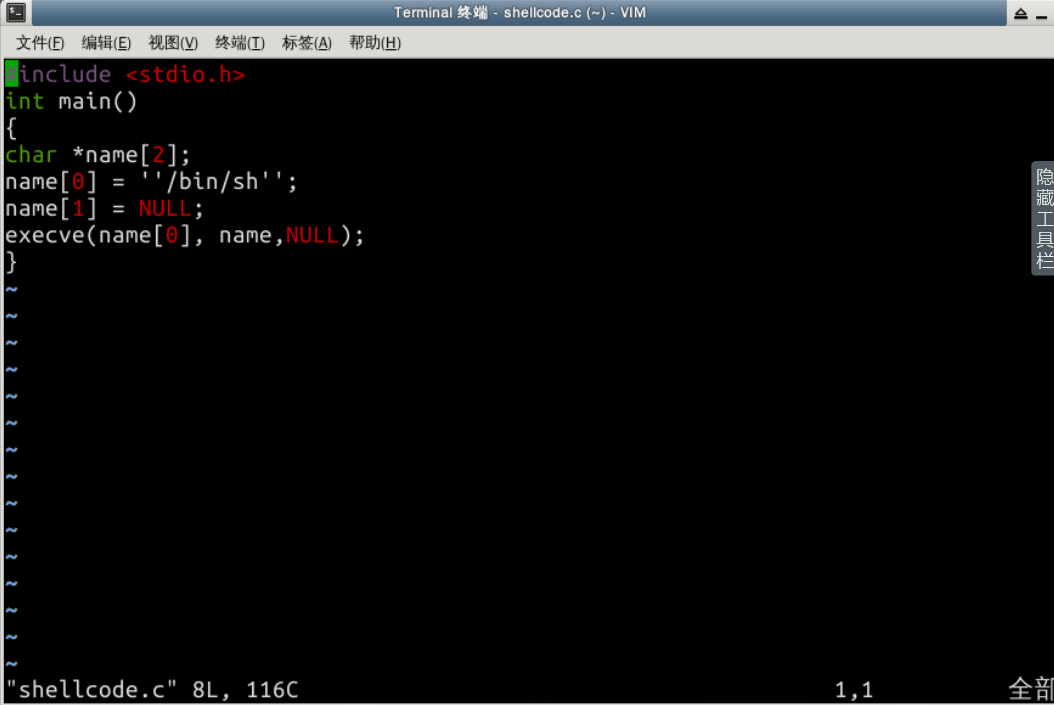
一般情况下，缓冲区溢出会造成程序崩溃，在程序中，溢出的数据覆盖了返回地址。而如果覆盖返回地址的数据是另一个地址，那么程序就会跳转到该地址，如果该地址存放的是一段精心设计的代码用于实现其功能，输入shellcode.c

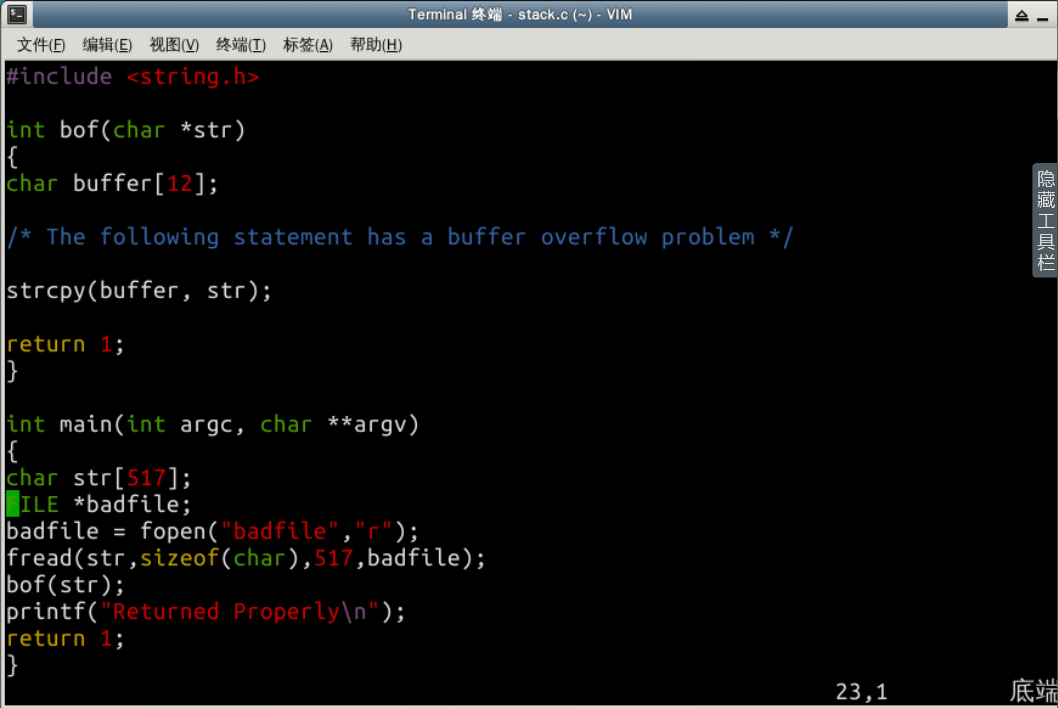
漏洞程序stack.c

程序会读取一个名为“badfile”的文件，并将文件内容装入“buffer”。

攻击程序exploit.c

“\x??\x??\x??\x??”
处需要添上shellcode保存在内存中的地址，因为发生溢出后这个位置刚好可以覆盖返回地址。
strcpy(buffer+100,shellcode); 这一句又告诉我们，shellcode保存在 buffer+100 的位置。
现在我们要得到shellcode在内存中的地址，需要gdb测试：

然后编译exploit.c程序：gcc -m32 -o exploit exploit.c

但不知道为什么我试了好几次，有出现段错误，然后又进行gdb测试，但后来一直出现“非法命令”，这点还未弄明白，后面我也会请教一下老师同学。

3、完成教材p97 2.96 2.97

2.96

题目：遵循位级浮点编码规则，实现如下原型的函数：

int float_f2i(float_bits f);

对于浮点数f，这个函数计算（int）f。如果f是NaN，你的函数一个向零舍入。如果f不能用整数表示（例如，超出表示范围，或者他是一个NaN），那么函数一应该返回0x80000000.测试你的函数，对参数f可以取得所有2^32个值求值，将结果与你使用的机器的浮点运算得到的结果相比较。

遇到的问题：

对‘pow’未定义的引用；导致编译不出来

解决过程：

使用math.h中声明的库函数还有一点特殊之处，gcc命令行必须加-lm选项，因为数学函数位于libm.so库文件中（这些库文件通常位于/lib目录下），-lm选项告诉编译器，我们程序中用到的数学函数要到这个库文件里找。

知道后加上-lm，编译成功了

代码托管

2.97

遵循位级浮点编码规则，实现具有如下原型的函数：

Compute (float) i
float_bitsfloat_i2f(inti);

对于参数i，这个函数计算(float)i的位级表示。
测试你的函数，对参数f可以取的所有2^32个值求值，将结果与你使用机器的浮点运算得到的结果相比较。

代码托管

进行编译：

运行结果：