【uoj#225】[UR #15]奥林匹克五子棋 构造

题目描述

两个人在 $n\times m$ 的棋盘上下 $k$ 子棋，问：是否存在一种平局的情况？如果存在则输出一种可能的最终情况。

输入

第一行三个正整数 $n,m,k$ ，意义如前所述。

输出

如果双方不能打成平局，输出 $−1$ ；

否则输出 $n×m$ 行，第 $i$ 行两个整数 $x_i,y_i$ 表示第 $i$ 次落子的坐标为第 $x_i$ 行第 $y_i$ 列。黑子先行，所以 $i$ 为奇数时为黑方落子，$i$ 为偶数时白方落子。坐标需满足 $1≤x_i≤n,1≤y_i≤m$ 。

样例输入

4 4 3

样例输出

1 2
1 1
1 4
1 3
2 1
2 3
2 2
2 4
3 3
3 2
3 4
3 1
4 1
4 4
4 3
4 2

---

题解

构造

显然 $k=1$ 时无解。

$k=2$ 当且仅当 $\text{min}(n,m)=1$ 时有解。因为若 $n>1,m>1$ ，对于一个 $2\times 2$ 的部分一定无法避免两个连续。

当 $k\ge 3$ 时，可以构造出如下的棋盘：

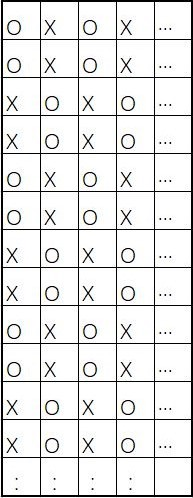
显然这其中包含连续的棋子数最多只有 $2$ 。

那么是否满足O与X相差不超过1呢？

容易发现只有 $n\mod 4=2$ （此时第一列会多填两个O）且 $m$ 为奇数时不成立，这种情况下把棋盘向上平移一排（即第一列从上至下是OXXOOXXOO...XXOOX）即可。

时间复杂度 $O(nm)$

#include <cstdio>
int ax[125010] , ay[125010] , at , bx[125010] , by[125010] , bt;
int main()
{
	int n , m , k , i , j;
	scanf("%d%d%d" , &n , &m , &k);
	if(k == 1) puts("-1");
	else if(k == 2)
	{
		if(n > 1 && m > 1) puts("-1");
		else
			for(i = 1 ; i <= n ; i ++ )
				for(j = 1 ; j <= m ; j ++ )
					printf("%d %d\n" , i , j);
	}
	else
	{
		if((n & 3) == 2 && m & 1)
		{
			for(i = 1 ; i <= n ; i ++ )
			{
				for(j = 1 ; j <= m ; j ++ )
				{
					if(((i & 3) > 1) == (j & 1)) ax[++at] = i , ay[at] = j;
					else bx[++bt] = i , by[bt] = j;
				}
			}
		}
		else
		{
			for(i = 1 ; i <= n ; i ++ )
			{
				for(j = 1 ; j <= m ; j ++ )
				{
					if(((i & 3) && ((i & 3) < 3)) == (j & 1)) ax[++at] = i , ay[at] = j;
					else bx[++bt] = i , by[bt] = j;
				}
			}
		}
		for(i = 1 ; i <= n * m ; i ++ )
		{
			if(i & 1) printf("%d %d\n" , ax[at] , ay[at]) , at -- ;
			else printf("%d %d\n" , bx[bt] , by[bt]) , bt -- ;
		}
	}
	return 0;
}