scikit-learn 学习笔记-- Generalized Linear Models （二）

Lasso regression

今天介绍另外一种带正则项的线性回归， ridge regression 的正则项是二范数，还有另外一种是一范数的，也就是lasso 回归，lasso 回归的正则项是系数的绝对值之和，这种正则项会让系数最后变得稀疏：

minw12N‖Xw−y‖22+α‖w‖1" role="presentation">minw12N∥Xw−y∥22+α∥w∥1minw12N‖Xw−y‖22+α‖w‖1

其中，N" role="presentation" style="position: relative;">NN 是样本的个数。

Elastic Net

Elastic Net 这种线性回归将二范数和一范数的正则都考虑进去了，两种正则项以某种权重的方式组合在一起，所以类似一种弹性的模型，这大概也是其名称的由来吧，elastic net 的目标函数为：

minw12N‖Xw−y‖22+αρ‖w‖1+α(1−ρ)2‖w‖22" role="presentation">minw12N∥Xw−y∥22+αρ∥w∥1+α(1−ρ)2∥w∥22minw12N‖Xw−y‖22+αρ‖w‖1+α(1−ρ)2‖w‖22

elastic net 模型可以让模型像 lasso regression 一样具有一定的稀疏性，同时又保持 ridge regression 的稳定性

import numpy as np
import matplotlib.pyplot as plt

from sklearn.metrics import r2_score

np.random.seed(42)

n_samples, n_features = 100, 100
X = np.random.randn(n_samples, n_features)

coef = 3 * np.random.randn(n_features)
inds = np.arange(n_features)
np.random.shuffle(inds)
coef[inds[10:]] = 0  # sparsify coef
y = np.dot(X, coef)

# add noise
y += 0.01 * np.random.normal(size=n_samples)

# Split data in train set and test set
n_samples = X.shape[0]
X_train, y_train = X[:n_samples // 2], y[:n_samples // 2]
X_test, y_test = X[n_samples // 2:], y[n_samples // 2:]

# #############################################################################
# Lasso
from sklearn.linear_model import Lasso

alpha = 0.1
lasso = Lasso(alpha=alpha)

y_pred_lasso = lasso.fit(X_train, y_train).predict(X_test)
r2_score_lasso = r2_score(y_test, y_pred_lasso)
print(lasso)
print("r^2 on test data : %f" % r2_score_lasso)

# #############################################################################
# ElasticNet
from sklearn.linear_model import ElasticNet

enet = ElasticNet(alpha=alpha, l1_ratio=0.7)

y_pred_enet = enet.fit(X_train, y_train).predict(X_test)
r2_score_enet = r2_score(y_test, y_pred_enet)
print(enet)
print("r^2 on test data : %f" % r2_score_enet)

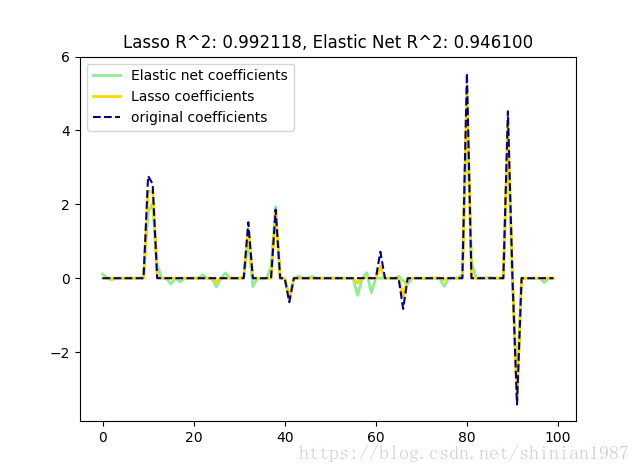
plt.plot(enet.coef_, color='lightgreen', linewidth=2,
         label='Elastic net coefficients')
plt.plot(lasso.coef_, color='gold', linewidth=2,
         label='Lasso coefficients')
plt.plot(coef, '--', color='navy', label='original coefficients')
plt.legend(loc='best')
plt.title("Lasso R^2: %f, Elastic Net R^2: %f"
          % (r2_score_lasso, r2_score_enet))
plt.show()

#########################
**output**：
Lasso(alpha=0.1, copy_X=True, fit_intercept=True, max_iter=1000,
   normalize=False, positive=False, precompute=False, random_state=None,
   selection='cyclic', tol=0.0001, warm_start=False)
r^2 on test data : 0.992118
ElasticNet(alpha=0.1, copy_X=True, fit_intercept=True, l1_ratio=0.7,
      max_iter=1000, normalize=False, positive=False, precompute=False,
      random_state=None, selection='cyclic', tol=0.0001, warm_start=False)
r^2 on test data : 0.946100
#########################