2017BUAA软工个人项目之数独生成与求解

1.项目GitHub地址：https://github.com/ZiJiaW/Soduko

（由于一开始把sudoku看成了soduko，于是名字建错了，读起来可能有点奇怪…）

2.项目PSP表格如下：

PSP2.1	Personal Software Process Stages	预估耗时	实际耗时
Planning	计划	0.5h	0.5h
.Estimate	.估计这个任务需要多少时间	0.5h	0.5h
Development	开发	20.5h	21.5
.Analysis	.需求分析（包括学习新技术）	3h	2h
.Design Spec	.生成设计文档	0h	0h
.Design Review	.设计复审（和同事设计审核设计文档）	0h	0h
.Coding Standard	.代码规范（为目前的开发指定合适的规范）	0h	0h
.Design	.具体设计	3h	2.5h
.Coding	.具体编码	8h	6h
.Code Review	.代码复审	0h	0h
.Test	.测试（自我测试，修改代码，提交修改）	2h	6h
Reporting	报告	3h	4h
.Test Reprot	.测试报告	1.5h	1h
.Size Measurement	.计算工作量	0.5h	0h
.Postmortem & Process Improvement Plan	.事后总结，并提出过程改进计划	1h	0.5h
	合计	24h	23h

3.解题思路

3.1 任务需求

编写命令行程序(sudoku.exe)，支持下列指令：1. sudoku.exe –c N  2. sudoku.exe  -s absolute_path_of_puzzlefile；

指令1实现程序生成不重复的N个数独终局至同目录下文件sudoku.txt，数独矩阵的左上角数字为确定的(9+6)%9+1=7；指令2将绝对路径下的数独题目解出并生成答案于同目录下的sudoku.txt。

3.2 思路分析

直觉告诉我解数独比较简单，所以我先想的是怎么解数独。查了下资料发现主要就两种方法，最简单的就是递归回溯，另外一种就是Dancing Links算法，将数独转化成精确覆盖问题求解，其实也是需要回溯的，但是使用的数据结构比较方便。因为我先想的也是递归填数，而且比较简单，所以就选择第一种方法了。思路很简单，将读取到的数独题目保存在9*9的二维数组中：

1. 从第一个格子开始填数，如果该格子已经填过，那么处理下一个格子；
2. 如果当前格子是空的，尝试从1-9中选择数字填入，并判断是否符合数独规则，符合则填入；
3. 若最终没有找到合适的数填入，说明在之前填的某一个数字不对，进行回溯。
4. 若填的是最后一个格子且满足规则，说明找到了数独的一个解，程序结束。

解决了解数独的问题，再来看怎么生成数独，其实从上面的角度很容易就想到，把初始的数独矩阵全部置零，按照解数独的方法即可生成数独了，只不过需要生成的数独数量较多，相当于求全零数独的前N个解，那么只要将解数独的算法步骤稍作修改，当生成的解是第N个，输出该解让程序结束，当生成的解不足N个时，输出该解并回溯，这样就能够保证已经生成的解不会二次生成，因为回溯后必然改变之前的某个值。至于左上角规则，只需要在预先放置好需要的数字，然后从第二个格子开始处理即可。

4.实现过程

分析需求，我设计了以下函数和类：

4.1输入

vector<int(*)[]> SodukoInput(char * filename);

读取文件中的数独题目，每一个题目为一个2维矩阵，返回各题目矩阵指针的vector；

4.2输出

void SudokuOutput(char *ret, int maxnum, char *ret2);

将得到的保存所有数独解的数组设置格式（空格和回车），然后返回之，使用fputs输出。

4.3数独求解模块

class SudokuSolve {
public:
    bool Solve(int r, int l);//递归填数
    bool check(int r, int l, int num);//测试同行同宫同列是否已有num
    void ProblemInit(int p[][]);//初始化
    int(*getSolution())[];//返回解
private:
    int problem[][];
};

每一个需要求解的数独初始化一个类，Solve函数即为对problem[r][l]的处理试填，check函数判断在problem[r][l]处填入num是否符合规则，getSolution用于在解决数独后返回填完的problem的指针，用于输出。

4.3数独生成模块

class SudokuMaker {
public:
    bool fill(int r, int l, char *ret);//递归填数
    bool check(int r, int l, int num);//判断在[r,l]处放入num是否符合数独规则
    void RequestInit(int n);//初始化需求
private:
    int maxnum;//需要生成的数独终局数
    int count;//当前已生成的数独终局数
    int M[][];//维护的数独棋盘
};

5.关键代码说明

下面给出数独求解的Solve函数进行说明：

bool SudokuSolve::Solve(int r, int l)
{
    int nr = l ==  ? r +  : r;
    int nl = l ==  ?  : l + ;
    if (problem[r][l] !=  && nr < )//(r, l) already has a number
    {
        if (SudokuSolve::Solve(nr, nl))
            return true;
        else
            return false;
    }
    else if (problem[r][l] !=  && nr >= )//problem solved
        return true;
    // now problem[i][j] == 0, try to fill it.
    for (int k = ; k < ; ++k)
    {
        if (!SudokuSolve::check(r, l, k))
            continue;
        problem[r][l] = k;
        if (r ==  && l == )//problem solved
            return true;
        if (SudokuSolve::Solve(nr, nl))
            return true;
        else
            problem[r][l] = ;//k is bad, try k+1.
    }
    return false;//can't find a k.
}

实际调用的时候，首先初始化数独题目，即函数中的problem，而后调用Solve(0,0)即可将problem解出；上面的函数首先计算当前处理位置的下一位置，若当前位置已经有值，则直接处理下一个，若恰好在最后一个位置有值，则说明此时数独已经解好了，可以结束递归；在当前位置为空时，我们就要尝试填数，对每一个判断是否符合规则，找到一个合适的值后，若填的是最后一个位置，同样说明数独解决；否则填值后处理下一个位置，若下一个位置的处理失败，说明当前位置的填值不合适，尝试下一个数；在尝试所有数后，若没有合适的，说明之前位置填值有误，需要恢复当前位置的空状态并回溯。注意恢复problem[r][l]=0是必要的，否则回溯到上一个位置时会对check函数（判断同行同列同宫是否存在k）的结果有影响，导致少解。

对这个函数的单元测试函数如下：

TEST_METHOD(TestMethod1)
        {
            int p[][] = { {,,,,,,,,},{,,,,,,,,},{,,,,,,,,},
            {,,,,,,,,},{,,,,,,,,},{,,,,,,,,},
            {,,,,,,,,},{,,,,,,,,},{,,,,,,,,} };
            SudokuSolve s;
            s.ProblemInit(p);
            s.Solve(, );
            int(*q)[] = s.getSolution();
            bool r = true;
            for (int i = ; i < ; ++i)
            {
                for (int j = ; j < ; ++j)
                    r &= s.check(i, j, q[i][j]);
            }
            Assert::AreEqual(r, true);
        }

使用的数独题目为号称最难的芬兰题，在实际运行中使用clock计时得到求解时间为245ms，测试中给出数独的解并测试其是否合法，测试结果如下：

相似的思路处理生成数独的问题，给出SudokuMaker::fill函数如下：

bool SudokuMaker::fill(int r, int l, char *ret)
{
    int nr = l ==  ? r +  : r;
    int nl = l ==  ?  : l + ;
    for (int k = ; k < ; ++k)
    {
        if (!SudokuMaker::check(r, l, k))
            continue;
        M[r][l] = k;
        if (r ==  && l == )//到达最后一个位置
        {
            count++;
            if (count == maxnum)//若已生成要求数目的数独终局，则输出终局并结束递归
            {
                for (int i = ; i < ; ++i)
                {
                    for (int j = ; j < ; ++j)
                    {
                        ret[ * i + j +  * (count-)] = char(M[i][j] + '');
                    }
                }
                return true;
            }
            else
            {
                //生成数目不够，则输出并恢复[r,l]处的值，并试填下一个
                for (int i = ; i < ; ++i)
                {
                    for (int j = ; j < ; ++j)
                    {
                        ret[ * i + j +  * (count-)] = char(M[i][j] + '');
                    }
                }
                M[r][l] = ;
                continue;
            }
        }
        else
        {
            if (SudokuMaker::fill(nr, nl, ret))//递归求解下一个位置
                return true;
            else
            {
                M[r][l] = ;
                continue;
            }
        }
    }
    return false;
}

可以看到两个函数布局差不多，实际上和之前分析的一样，初始化数组M的左上角，从位置(0,1)开始求解，两者的区别在于前者只要得到一个可行解就可以输出结束递归，而后者需要生成maxnum个数独终局，因此在生成足够数目的数独前，函数一律在输出后继续尝试，尝试所有的值后回溯。下面给出代码覆盖率测试结果，分两块，一块是生成数独，一块是解数独：

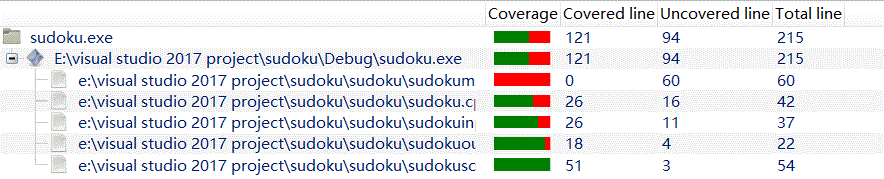
因为一次只能设置一个命令行参数，所以都不是100%，但是可以看到两个模块分别都是覆盖率很高的。

6.性能分析和改进

由于选择的是暴力回溯，瓶颈在那里，所以数独生成的速度肯定不会很快…但是按照以上的思路编译通过后第一次性能分析，我选择的是生成1000个数独终局，运行时间达到了惊人的38秒，我瞬间有了跳崖的冲动。仔细查看性能分析结果，我发现程序98%以上的时间在做文件IO（最初版本性能测试没有截图），于是我仔细查看了我的IO函数，实际上我的IO是在每生成一个数组的时候进行输出，由于写的比较快，就直接在函数内进行文件的打开和关闭了，所以输出1000个数独需要开闭文件1000次，我将文件流传入函数，在外面开闭文件，速度就上去了。此时100000个数独需要1分钟左右，仍然很慢，下面是这时的输出函数。

void SudokuOutput(int p[][], bool flag, fstream &file)
{
    if (!file.is_open())
        cerr << "fail to open file!" << endl;
    else
    {
        for (int i = ; i < ; ++i)
        {
            for (int j = ; j < ; ++j)
            {
                if (j == )
                    file << p[i][j] << endl;
                else
                    file << p[i][j] << ' ';
            }
        }
        if (flag)
            file << endl;
    }
}

再次进行性能分析，发现程序运行时间依然是文件IO占了大头，这是突然想到这里是直接将数字以整型输出到文件，如果我把它改成字符输出呢？当即把p[i][j]改成char(p[i][j]+’0’),发现输出快了十几秒。继续分析发现操作符<<和endl的耗时很长，查阅资料，这里endl的flush作用是不需要的，所以将endl改成file.put(‘\n’),前者同理，到这里再运行，100000级的时间是14秒。但是还是很慢。由于我选择的算法十分的暴力，所以我预期百万级的测试在1分钟内完成，十万级就耗时14秒是不行的。机缘巧合之下又看到了这篇文章，于是试用了freopen重定向和putchar的组合，运行时间优化到9秒，确实有效果。这时又看到微信群里罗老师建议保存答案到最后一起输出，于是我尝试建了一个全局字符数组，将所有终局都存进去，在最后的时候直接用fputs全部输出，这时运行100000级输出运行时间为：5.121s，百万级为：49.553s（用clock计时）。满足预期了……到这里Output函数已经面目全非，被我改成给输出的数组添加空格和回车的函数了，就不贴了，但是之前贴的关键函数都是最终版。下面是性能分析结果（-c 100000）：

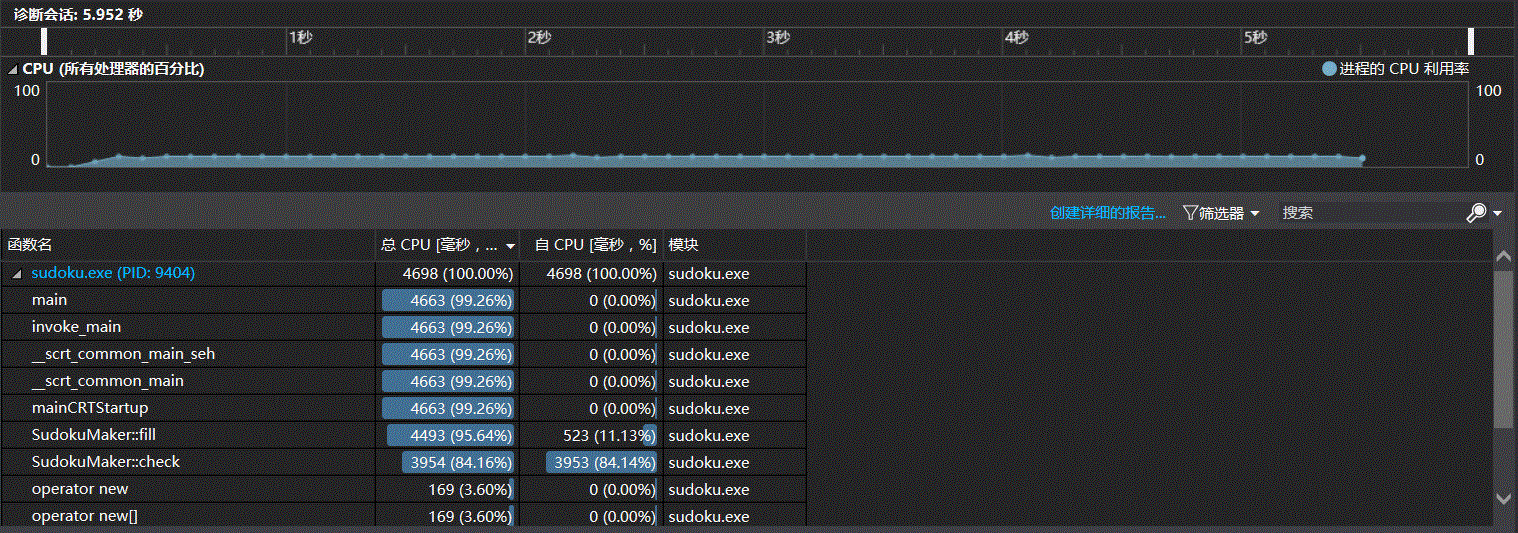
可以看到在优化IO后，IO占的时间很少了，现在最耗时的在于每次试填都要使用的check函数，用于判断同行同宫同列是否符合需求，我尝试过维护专门的数组来记录每行每列每宫已填数的信息，这样check函数就只需要查询这些数组了，但是实际测试下来和最简单的直接遍历行列宫相差无几，因为维护这些数组同样需要时间成本，所以最终按照原方案。

7.PSP各模块实际花费时间（略，见1）

8.感想

俗话说得好，不作死就不会死，暴力回溯生成数独终局确实是挺慢的，比不上各种取巧的方法，但是用来解数独我倒觉得是最实用也是最简单的方法，因为解数独是无法避免回溯和试填的。在写这个程序之前，说实话我没怎么用C++写过程序，计院的面向对象也还没上过，撑死了用C++解过几十道LeetCode，只能说略懂C++的语法而已，可以说是相当的菜了。前面写的优化其实只是对IO作了优化，对大佬们来说可以说是相当trivial了，但是对我来说，之前确实没有过处理这么多数据的情况，所以其实收获还是蛮大的，因为很多东西都是第一次用，包括VS和GitHub。最后，图简单暴力解题我觉得我大概要倒数了吧……