在PBN旁切转弯的基础上，再来看飞越转弯接TF（或CF）航段，保护区结构上有些相似，只是转弯拐角处的保护区边界有“简化”，其余部分是相近的。

FlyOver接TF段的标称航迹有一个飞越之后转弯切入航迹的过程，FlyBy是通过计算提前转弯量，一次性转弯完成切入下一段。

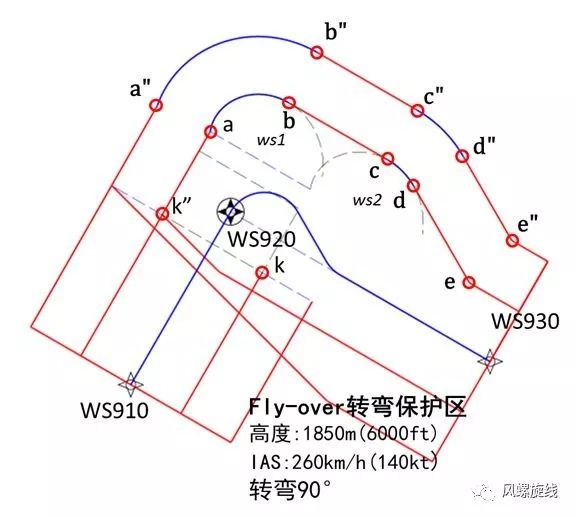
按照字母顺序对相关的风螺旋上的点进行标注，可以得到如图所示的a\b\c\d等位置点。与Flyby转弯一样，图中的a”点是a点按照0.5倍的保护区半宽外扩后的风螺旋与直线的交点，它不是a点的直接外扩点，在计算时可以采用迭代计算的方法进行求解。

（注：当副区外扩距离不是0.5倍的保护区半宽时，a”点的计算会更复杂一些，后续的b”点、c”点均与a”点对应的外扩距离相关。）

b点是从a点开始绘制的风螺旋旋转至90°+DA时的位置点。线段bc是两条风螺旋的公切线，b点与c点对应的sita值都等于90°+DA。

图中d点是按照30°内收线与风螺旋的切点，它所对应的sita 角度计算过程为：出航角度+30°-90°+ DA -（入航角度 – 90°）= 转弯角度 + 30°+DA 。

图中的d”点是副区外边界风螺旋与30°内收线的交点，它所对应的sita角度与d点相同，即sita等于转弯角度+ 30°+DA。

e点及e”点是30°内收线与后一段主/副区边界线的交点，可通过直线相交的计算方法得到。

当逐渐减少转弯角度时，e”会逐渐向d”靠拢，最终重合，之后e”点继续向c”靠拢，主区对应点会有相应的变化，需要具体分析。

总体来说，a”点与d”点若是通过保护区边界与风螺旋直接相交得到的时候，需要通过迭代计算来获得准确数据。其它的位置点如b”、c”（若存在的话）可以直接通过数学公式确定计算得到。

相关话题：

一张图读懂PBN旁切转弯计算

PBN参考模板--旁切转弯保护区

PBN参考模板--Flyover转弯衔接TF、CF航段

PBN参考模板--Flyover转弯衔接DF航段

9月1号，开学第一天，是一个很特别的日子。如果未来某一天，等距螺旋的概念可以成为几何课本的一部分，那该是多么开心的一件事情，我将为此而努力！

 

 

微信扫一扫
关注该公众号

一张图读懂PBN飞越转弯衔接TF/CF航段计算的更多相关文章

  1. 一张图读懂PBN飞越转弯衔接DF航段计算

    飞越转弯衔接TF航段时,转弯外边界与旁切转弯相似,只是在拐角位置直接以风螺旋绘制外边界,大部分切点可以精确计算得到. 飞越转弯衔接DF航段时,转弯外边界全部由风螺旋和它的切线构成,又会有哪些神奇的事情 ...

  2. 一张图读懂PBN旁切转弯计算

    当DOC8168进入PBN章节以后,所有的保护区不再标注风螺旋的字母位置点.似乎ICAO已经有了精确计算的方法,只是没有告诉我们.沿着风螺旋的轨迹一路走来,切线与角度的换算方法想必已经相当熟悉了吧,这 ...

  3. 一张图读懂https加密协议

    搭建CA服务器和iis启用https:http://blog.csdn.net/dier4836/article/details/7719532 一张图读懂https加密协议 https是一种加密传输 ...

  4. 比传统事务快10倍？一张图读懂阿里云全局事务服务GTS

    近日,阿里云全局事务服务GTS正式上线,为微服务架构中的分布式事务提供一站式解决方案.GTS的原理是将分布式事务与具体业务分离,在平台层面开发通用的事务中间件GTS,由事务中间件协调各服务的调用一致性 ...

  5. 一张图读懂Java多线程

    1.带着疑问看图 1)竞争对象的锁和竞争CPU资源以及竞争被唤醒 2)何种情况下获取到了锁,何种情况下会释放锁 2.还是那张图 3.详细图解 1)Thread t = new Thread(),初始化 ...

  6. 基础知识《零》---一张图读懂JDK,JRE,JVM的区别与联系

  7. PBN飞越转弯Flyover衔接DF航段保护区组图

    PBN飞越转弯Flyover衔接DF航段,是飞越转弯中最常用的形态. Flyover-DF保护区叠加图: Flyover-DF保护区分解图:

  8. PBN飞越转弯Flyover衔接TF、CF航段保护区组图

    PBN飞越转弯Flyover衔接TF.CF航段虽不常用,但也很重要,与旁切转弯有一定的相似性. 飞越转弯 flyover-TF/CF 叠加图: 飞越转弯 flyover-TF/CF 分解图:

  9. 一张图看懂Function和Object的关系及简述instanceof运算符

    我在写一篇图解prototype和__proto__的区别时,搜资料搜到了一个有意思的现象,下面这两个运算返回的结果是一样的: Function instanceof Object;//true Ob ...

随机推荐

  1. AX_UserInfo

    UserInfoHelp::userInUserGroup(curuserid(), "Admin")  EmplTable::userId2EmplId(curuserid()) ...

  2. Mac 电脑设置显示路径

    # 设置 defaults write com.apple.finder _FXShowPosixPathInTitle -bool TRUE;killall Finder # 删除 defaults ...

  3. 《Linux就该这么学》第八天课程

        当一个人的心中,有着更高的山峰想要去攀登时,他就不会在意脚下的泥沼. 今天发一下干货,常用命令的一些总结,今天的理论知识比较多. 原创地址:https://www.linuxprobe.com ...

  4. JAVA 8 主要新特性 ----------------(四)Lambda函数式接口

    一.什么是函数式接口 只包含一个抽象方法的接口,称为函数式接口.  你可以通过 Lambda 表达式来创建该接口的对象.(若 Lambda 表达式抛出一个受检异常,那么该异常需要在目标接口的抽象方法 ...

  5. Hdp安装问题杂解

    5.在安装的时候遇到的问题 5.1使用ambari-server start的时候出现ERROR: Exiting with exit code -1. 5.1.1REASON: Ambari Ser ...

  6. Android-broadcast静态动态广播

    广播的静态和动态类型 静态广播: 1.继承之broadcastreceiver public class MyStaticBroadcastReceiver extends BroadcastRece ...

  7. 桌面应用开发之WPF动态背景

      因为项目需要,在WPF开发的桌面应用中,登陆页面需使用动态背景.由于没有前端开发人员,所以由半吊子的后端开发人员根据效果图写前端xaml.去掉页面上边框,抽离动态背景设置代码: <Windo ...

  8. veri HDL modeisim仿真：test bench文件编写

    预编译指令: verilog HDL预编译指令是以" ' "字符开头,而且不需要以";"结尾. 作用:指示在编译verilog hdl源代码前,需要执行哪些操作 ...

  9. 【洛谷4070】 [SDOI2016]生成魔咒（SAM）

    传送门 洛谷 Solution 考虑要求的是什么,前缀的本质不同的字符串个数? 如果只要求一个串那么显然答案是\(\sum_{i=1}^{tot}len[i]-len[fa[i]]\)(实际上这个并不 ...

  10. 「ZJOI2018」胖（ST表+二分）

    「ZJOI2018」胖(ST表+二分) 不开 \(O_2\) 又没卡过去是种怎么体验... 这可能是 \(ZJOI2018\) 最简单的一题了...我都能 \(A\)... 首先我们发现这个奇怪的图每 ...