梯度下降法原理与python实现
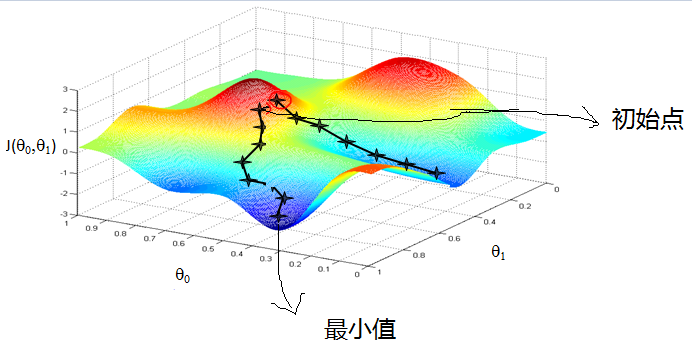
- 梯度下降法(Gradient descent)是一个一阶最优化算法,通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索,则会接近函数的局部极大值点;这个过程则被称为梯度上升法。
- 本文将从最优化问题谈起,回顾导数与梯度的概念,引出梯度下降的数据推导;概括三种梯度下降方法的优缺点,并用Python实现梯度下降(附源码)。
1 最优化问题
- 最优化问题是求解函数极值的问题,包括极大值和极小值。
- 微积分为我们求函数的极值提供了一个统一的思路:找函数的导数等于0的点,因为在极值点处,导数必定为0。这样,只要函数的可导的,我们就可以用这个万能的方法解决问题,幸运的是,在实际应用中我们遇到的函数基本上都是可导的。
- 机器学习之类的实际应用中,我们一般将最优化问题统一表述为求解函数的极小值问题,即:
\]
- 其中\(x\)称为优化变量,\(f\)称为目标函数。极大值问题可以转换成极小值问题来求解,只需要将目标函数加上负号即可:
\]
2 导数与梯度
- 梯度是多元函数对各个自变量偏导数形成的向量。多元函数的梯度表示:
\]
如果Hessian矩阵正定,函数有极小值;如果Hessian矩阵负定,函数有极大值;如果Hessian矩阵不定,则需要进一步讨论。
如果二阶导数大于0,函数有极小值;如果二阶导数小于0,函数有极大值;如果二阶导数等于0,情况不定。
问题:为何不直接求导,令导数等于零去求解?
- 直接求函数的导数,有的函数的导数方程组很难求解,比如下面的方程:
\]
3 梯度下降的推导过程
- 回顾一下泰勒展开式
\]
- 多元函数\(f(x)\)在x处的泰勒展开:
\]
3.1 数学推导
目标是求多元函数\(f(x)\)的极小值。梯度下降法是通过不断迭代得到函数极小值,即如能保证\(f(x +\Delta x)\)比\(f(x)\)小,则不断迭代,最终能得到极小值。想象你在山顶往山脚走,如果每一步到的位置比之前的位置低,就能走到山脚。问题是像哪个方向走,能最快到山脚呢?
由泰勒展开式得:
\]
如果\(\Delta x\)足够小,可以忽略\(o(\Delta x)\),则有:
\]
于是只有:
\]
能使
\]
因为\(\nabla f(x)\)与\(\Delta x\)均为向量,于是有:
\]
其中,\(\theta\)是向量\(\nabla f(x)\)与\(\Delta x\)的夹角,\(\| \nabla f(x)\|\)与\(\|\Delta x\|\)是向量对应的模。可见只有当
\]
才能使得
\]
又因
\]
可见,只有当
\]
即\(\theta = \pi\)时,函数数值降低最快。此时梯度和\(\Delta x\)反向,即夹角为180度。因此当向量\(\Delta x\)的模大小一定时,取
\]
即在梯度相反的方向函数值下降的最快。此时函数的下降值为:
\]
只要梯度不为\(0\),往梯度的反方向走函数值一定是下降的。直接用可能会有问题,因为\(x+\Delta x\)可能会超出\(x\)的邻域范围之外,此时是不能忽略泰勒展开中的二次及以上的项的,因此步伐不能太大。
一般设:
\]
其中\(\alpha\)为一个接近于\(0\)的正数,称为步长,由人工设定,用于保证\(x+\Delta x\)在x的邻域内,从而可以忽略泰勒展开中二次及更高的项,则有:
\]
此时,\(x\)的迭代公式是:
\]
只要没有到达梯度为\(0\)的点,则函数值会沿着序列\(x_{k}\)递减,最终会收敛到梯度为\(0\)的点,这就是梯度下降法。
迭代终止的条件是函数的梯度值为\(0\)(实际实现时是接近于\(0\)),此时认为已经达到极值点。注意我们找到的是梯度为\(0\)的点,这不一定就是极值点,后面会说明。
4 实现的细节
初始值的设定
一般的,对于不带约束条件的优化问题,我们可以将初始值设置为0,或者设置为随机数,对于神经网络的训练,一般设置为随机数,这对算法的收敛至关重要。学习率的设定
学习率设置为多少,也是实现时需要考虑的问题。最简单的,我们可以将学习率设置为一个很小的正数,如0.001。另外,可以采用更复杂的策略,在迭代的过程中动态的调整学习率的值。比如前1万次迭代为0.001,接下来1万次迭代时设置为0.0001。
5 存在的问题
- 局部极小值
- 梯度下降可能在局部最小的点收敛。
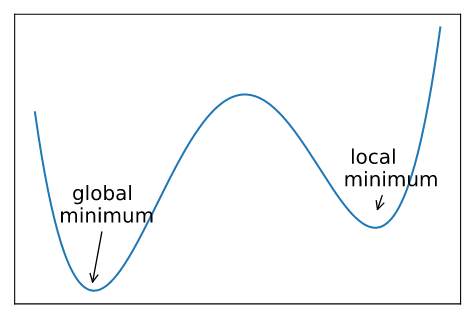
- 梯度下降可能在局部最小的点收敛。
- 鞍点
- 鞍点是指梯度为0,Hessian矩阵既不是正定也不是负定,即不定的点。如函数\(x^2-y^2\)在\((0,0)\)点梯度为0,但显然不是局部最小的点,也不是全局最小的点。
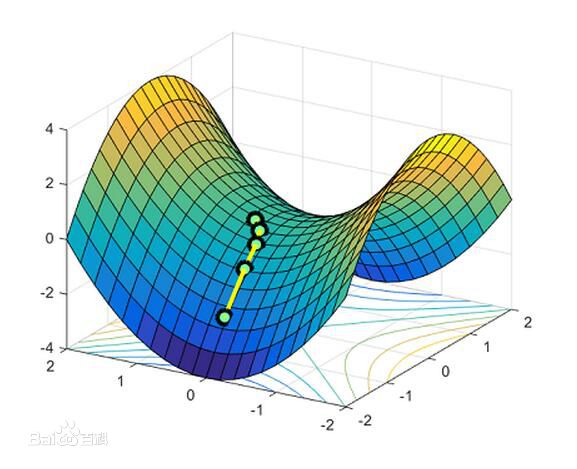
- 鞍点是指梯度为0,Hessian矩阵既不是正定也不是负定,即不定的点。如函数\(x^2-y^2\)在\((0,0)\)点梯度为0,但显然不是局部最小的点,也不是全局最小的点。
6 三种梯度下降的实现
- 批量梯度下降法:Batch Gradient Descent,简称BGD。求解梯度的过程中用了全量数据。
- 全局最优解;易于并行实现。
- 计算代价大,数据量大时,训练过程慢。
- 随机梯度下降法:Stochastic Gradient Descent,简称SGD。依次选择单个样本计算梯度。
- 优点:训练速度快;
- 缺点:准确度下降,并不是全局最优;不易于并行实现。
- 小批量梯度下降法:Mini-batch Gradient Descent,简称MBGD。每次更新参数时使用b个样本。(b一般为10)。
- 两种方法的性能之间取得一个折中。
7 用梯度下降法求解多项式极值
7.1 题目
\(argmin\frac{1}{2}[(x_{1}+x_{2}-4)^2 + (2x_{1}+3x_{2}-7)^2 + (4x_{1}+x_{2}-9)^2]\)
7.2 python解题
以下只是为了演示计算过程,便于理解梯度下降,代码仅供参考。更好的代码我将在以后的文章中给出。
# 原函数
def argminf(x1, x2):
r = ((x1+x2-4)**2 + (2*x1+3*x2 - 7)**2 + (4*x1+x2-9)**2)*0.5
return r
# 全量计算一阶偏导的值
def deriv_x(x1, x2):
r1 = (x1+x2-4) + (2*x1+3*x2-7)*2 + (4*x1+x2-9)*4
r2 = (x1+x2-4) + (2*x1+3*x2-7)*3 + (4*x1+x2-9)
return r1, r2
# 梯度下降算法
def gradient_decs(n):
alpha = 0.01 # 学习率
x1, x2 = 0, 0 # 初始值
y1 = argminf(x1, x2)
for i in range(n):
deriv1, deriv2 = deriv_x(x1, x2)
x1 = x1 - alpha * deriv1
x2 = x2 - alpha * deriv2
y2 = argminf(x1, x2)
if y1 - y2 < 1e-6:
return x1, x2, y2
if y2 < y1:
y1 = y2
return x1, x2, y2
# 迭代1000次结果
gradient_decs(1000)
# (1.9987027392533656, 1.092923742270406, 0.4545566995437954)
参考文献
- 《机器学习与应用》
- https://zh.wikipedia.org/wiki/梯度下降法
梯度下降法原理与python实现的更多相关文章
- 梯度下降法实现(Python语言描述)
原文地址:传送门 import numpy as np import matplotlib.pyplot as plt %matplotlib inline plt.style.use(['ggplo ...
- 机器学习中梯度下降法原理及用其解决线性回归问题的C语言实现
本文讲梯度下降(Gradient Descent)前先看看利用梯度下降法进行监督学习(例如分类.回归等)的一般步骤: 1, 定义损失函数(Loss Function) 2, 信息流forward pr ...
- 梯度下降法的python代码实现(多元线性回归)
梯度下降法的python代码实现(多元线性回归最小化损失函数) 1.梯度下降法主要用来最小化损失函数,是一种比较常用的最优化方法,其具体包含了以下两种不同的方式:批量梯度下降法(沿着梯度变化最快的方向 ...
- 对数几率回归(逻辑回归)原理与Python实现
目录 一.对数几率和对数几率回归 二.Sigmoid函数 三.极大似然法 四.梯度下降法 四.Python实现 一.对数几率和对数几率回归 在对数几率回归中,我们将样本的模型输出\(y^*\)定义 ...
- 机器学习入门-BP神经网络模型及梯度下降法-2017年9月5日14:58:16
BP(Back Propagation)网络是1985年由Rumelhart和McCelland为首的科学家小组提出,是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一. B ...
- BP神经网络模型及梯度下降法
BP(Back Propagation)网络是1985年由Rumelhart和McCelland为首的科学家小组提出,是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一. B ...
- 固定学习率梯度下降法的Python实现方案
应用场景 优化算法经常被使用在各种组合优化问题中.我们可以假定待优化的函数对象\(f(x)\)是一个黑盒,我们可以给这个黑盒输入一些参数\(x_0, x_1, ...\),然后这个黑盒会给我们返回其计 ...
- 梯度下降法VS随机梯度下降法 (Python的实现)
# -*- coding: cp936 -*- import numpy as np from scipy import stats import matplotlib.pyplot as plt # ...
- 梯度下降法实现-python[转载]
转自:https://www.jianshu.com/p/c7e642877b0e 梯度下降法,思想及代码解读. import numpy as np # Size of the points dat ...
随机推荐
- 谷歌开源的一个BTREE实现 Go语言
// Copyright 2014 Google Inc. // // Licensed under the Apache License, Version 2.0 (the "Licens ...
- 【APP测试(Android)】--客户端数据库
- 登录服务器失败 IP 统计和处理方法
一.登录ssh失败次数统计 1)错误的打开方式 awk '/Failed password/ {print $(NF-3)}' secure |sort -n |uniq -c|sort -n |ta ...
- 20175316盛茂淞 2018-2019-2 《Java程序设计》第5周学习总结
20175316盛茂淞 2018-2019-2 <Java程序设计>第5周学习总结 教材学习内容总结 第六章 接口与实现. 何谓接口 接口:书上没有明确地给出接口的定义,我理解的接口就是一 ...
- 64位版本为什么叫amd64,而不是intel64
64位版本为什么叫amd64,而不是intel64? 首先了解下常见的几个架构: X86是一个指令集,是刚有个人电脑时候的什么8086,286,386的那个兼容的指令集. “x86-64”,有时会 ...
- Navicat导入.xls等文件失败
一.问题 在学习django的models时,使用Navicat premium导入.xls数据的时候会出现导入失败的原因,即使是换成了csv文件也是失败的,原因是数据库的表有外键,而需要设置外键限制 ...
- mui几种页面跳转方式对比
1.初始化时创建子页面 mui.init({ subpages: [{ url: your - subpage - url, //子页面HTML地址,支持本地地址和网络地址 id: your - su ...
- easyui中的option设置selected没有效果
在mvc中,使用了easyUI框架,然后我点击添加新消息的时候弹窗一个新窗口,添加信息.却发现我的select一直无法设置默认状态,jq选中,还是直接在添加一条请选择的option都没办法选中,网络上 ...
- android 测试
Android Monkey压力测试 monkey测试结果详细分析 Android自动化测试工具 UiAutomator使用详解 在Android Sudio中使用Uiautomator 六款Andr ...
- 用Rider写一个有IOC容器Autofac的.net core的程序
一:Autofac是一个和Java里的Spring IOC容器一样的东西,不过它确实没有Spring里的那么方便,主要是在于它没有提供足够的Api和扫描方式等等,不过优点是它比Spring要快很多,而 ...
