Normal Equation of Computing Parameters Analytically

Normal Equation

Note: [8:00 to 8:44 - The design matrix X (in the bottom right side of the slide) given in the example should have elements x with subscript 1 and superscripts varying from 1 to m because for all m training sets there are only 2 features x0 and x1. 12:56 - The X matrix is m by (n+1) and NOT n by n. ]

Gradient descent gives one way of minimizing J. Let’s discuss a second way of doing so, this time performing the minimization explicitly and without resorting to an iterative algorithm. In the "Normal Equation" method, we will minimize J by explicitly taking its derivatives with respect to the θj ’s, and setting them to zero. This allows us to find the optimum theta without iteration. The normal equation formula is given below:

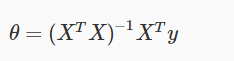
There is no need to do feature scaling with the normal equation.

The following is a comparison of gradient descent and the normal equation:

With the normal equation, computing the inversion has complexity 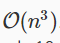 So if we have a very large number of features, the normal equation will be slow. In practice, when n exceeds 10,000 it might be a good time to go from a normal solution to an iterative process.

Normal Equation Noninvertibility

When implementing the normal equation in octave we want to use the 'pinv' function rather than 'inv.' The 'pinv' function will give you a value of θ even if 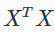 is not invertible.

If 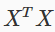 is noninvertible, the common causes might be having :

• Redundant features, where two features are very closely related (i.e. they are linearly dependent)
• Too many features (e.g. m ≤ n). In this case, delete some features or use "regularization" (to be explained in a later lesson).

Solutions to the above problems include deleting a feature that is linearly dependent with another or deleting one or more features when there are too many features.