洛谷 P2046 BZOJ 2007 海拔(NOI2010)

题目描述

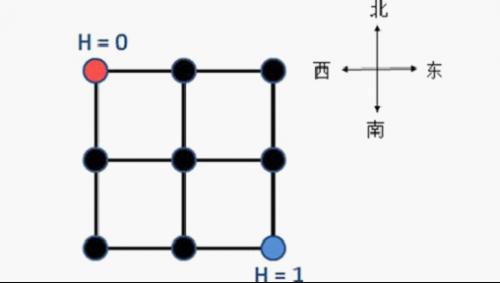
YT市是一个规划良好的城市，城市被东西向和南北向的主干道划分为n×n个区域。简单起见，可以将YT市看作 一个正方形，每一个区域也可看作一个正方形。从而，YT城市中包括(n+1)×(n+1)个交叉路口和2n×(n+1)条双向道路（简称道路），每条双向 道路连接主干道上两个相邻的交叉路口。下图为一张YT市的地图(n = 2)，城市被划分为2×2个区域，包括3×3个交叉路口和12条双向道路。

小Z作为该市的市长，他根据统计信息得到了每天上班高峰期间YT市每条道路两个方向的人流量，即在高峰期间沿 着该方向通过这条道路的人数。每一个交叉路口都有不同的海拔高度值，YT市市民认为爬坡是一件非常累的事情，每向上爬h的高度，就需要消耗h的体力。如果 是下坡的话，则不需要耗费体力。因此如果一段道路的终点海拔减去起点海拔的值为h(注意h可能是负数)，那么一个人经过这段路所消耗的体力是max{0, h}（这里max{a, b}表示取a, b两个值中的较大值）。

小Z还测量得到这个城市西北角的交叉路口海拔为0，东南角的交叉路口海拔为1(如上图所示)，但其它交叉路口的海拔高度都无法得知。小Z想知道在最理想的情况下（即你可以任意假设其他路口的海拔高度），每天上班高峰期间所有人爬坡消耗的总体力和的最小值。

输入输出格式

输入格式：

第一行包含一个整数n，含义如上文所示。

接下来4n(n + 1)行，每行包含一个非负整数分别表示每一条道路每一个方向的人流量信息。输入顺序：n(n + 1)个数表示所有从西到东方向的人流量，然后n(n + 1)个数表示所有从北到南方向的人流量，n(n + 1)个数表示所有从东到西方向的人流量，最后是n(n + 1)个数表示所有从南到北方向的人流量。对于每一个方向，输入顺序按照起点由北向南，若南北方向相同时由西到东的顺序给出(参见样例输入)。

输出格式：

仅包含一个数，表示在最理想情况下每天上班高峰期间所有人爬坡所消耗的总体力和（即总体力和的最小值），结果四舍五入到整数。

输入输出样例

输入样例#1：

1
1
2
3
4
5
6
7
8

输出样例#1：

3

说明

对于20%的数据：n ≤ 3；

对于50%的数据：n ≤ 15；

对于80%的数据：n ≤ 40；

对于100%的数据：1 ≤ n ≤ 500，0 ≤ 流量 ≤ 1,000,000且所有流量均为整数。

吐槽

　　吐槽恶心的输入……

　　BZOJ所有点一起评测，算总时间，我写spfa跑了8000+ms，交到洛谷上就TLE了两个点，给spfa加了SLF优化，依然只能8个点，再去大牛分站开O2，过了9个点。假设BZOJ和洛谷给我评测的那台评测机速度一样，洛谷#1到#9我总共跑了1500ms左右，那么#10我的要跑6000ms+啊，害怕……

　　spfa的LLL优化写这题得不偿失，代码长了容易错，反正也没负边权，就写了dijkstra，我用了最裸的堆优化，在洛谷主站(无O2)跑了1137ms，当时洛谷rank24，再去大牛分站开O2跑一波，409ms，正好rank10，看了看rank1的200+ms，那位dalao用的是algorithm里的heap，好像这玩意跑得比手写二叉堆还快，过几天学一下，不知道可不可以像pb_ds中的配对对一样无脑替代priority_queue。虽然平板电视里的配对堆快得多，但我嫌pb_ds使用方法过于复杂，单词太难背了……

解题思路

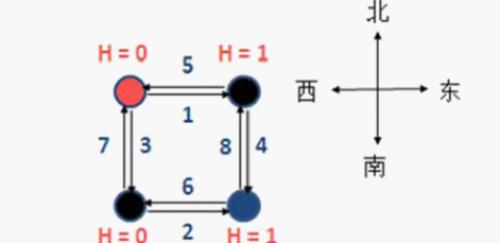
　　像BZOJ 1001狼爪兔子一样，本来是求原图最大流，但数据范围过大，会被卡。由于两题的图都是平面图，所以可以建对偶图，然后在对偶图上跑最短路(最小割)

源代码

1、spfa加SLF优化//不加这个优化在BZOJ、cogs上都能过了

#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

int n;

struct Edge{
    int next,to,w;
}e[];
int cnt=,head[]={};
void add(int u,int v,int w)
{
    e[cnt]={head[u],v,w};
    head[u]=cnt++;
}
int s,t;
int dis[];
bool inq[]={};
int spfa()
{
    memset(dis,0x7f,sizeof(dis));
    queue<int> q;
    dis[s]=;
    inq[s]=;
    q.push(s);
    while(!q.empty())
    {
        int u=q.front();q.pop();
        inq[u]=;
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to,w=e[i].w;
            if(dis[v]>dis[u]+w)
            {
                dis[v]=dis[u]+w;
                if(!inq[v])
                {
                    q.push(v);
                    inq[v]=;
                }
            }
        }
    }
    return dis[t];
}

int main()
{
    //freopen("altitude.in","r",stdin);
    //freopen("altitude.out","w",stdout);
    scanf("%d",&n);
    s=n*n+,t=n*n+;
    /***从左到右***/
    for(int i=,w;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            scanf("%d",&w);
            if(i==)
                add(s,(j-)*n+,w);
            else if(i==n)
                add(j*n,t,w);
            else
                add((j-)*n+i,(j-)*n+i+,w);
        }
    }
    /******/
    /***从上到下***/
    for(int i=,w;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            scanf("%d",&w);
            if(j==)
                add(i,t,w);
            else if(j==n)
                add(s,i+n*(n-),w);
            else
                add(j*n+i,(j-)*n+i,w);
        }
    }
    /******/

    /***从右向左***/
    for(int i=,w;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            scanf("%d",&w);
            if(i==)
                add((j-)*n+,s,w);
            else if(i==n)
                add(t,j*n,w);
            else
                add((j-)*n+i+,(j-)*n+i,w);
        }
    }
    /******/

    /***从下到上***/
    for(int i=,w;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            scanf("%d",&w);
            if(j==)
                add(t,i,w);
            else if(j==n)
                add(i+n*(n-),s,w);
            else
                add((j-)*n+i,j*n+i,w);
        }
    }
    /******/
    /*for(int i=1;i<=n*n+2;i++)
    {
        for(int j=head[i];j;j=e[j].next)
            printf("%d=>%d %d\n",i,e[j].to,e[j].w);
    }*///输出建好的图
    /***没啦***/
    printf("%d\n",spfa());
    return ;
}

2、堆优化的dijkstra

#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>

int n;

struct Edge{
    int next,to,w;
}e[];
int cnt=,head[]={};
void add(int u,int v,int w)
{
    e[cnt]={head[u],v,w};
    head[u]=cnt++;
}
int s,t;
int dis[];
bool vis[]={};
struct P{
    int u,D;
    bool operator < (const P & a)const{
        return D>a.D;
    }
}temp;
int dijkstra()
{
    memset(dis,0x7f,sizeof(dis));
    dis[s]=;
    std::priority_queue<P> q;
    q.push({s,});
    while(!q.empty())
    {
        temp=q.top();
        q.pop();
        int u=temp.u,D=temp.D;
        if(vis[u]) continue;
        vis[u]=;
        for(int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(dis[v]>D+e[i].w)
            {
                dis[v]=D+e[i].w;
                q.push({v,dis[v]});
            }
        }
    }
    return dis[t];
}

int main()
{
    //freopen("altitude.in","r",stdin);
    //freopen("altitude.out","w",stdout);
    scanf("%d",&n);
    s=n*n+,t=n*n+;
    /***从左到右***/
    for(int i=,w;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            scanf("%d",&w);
            if(i==)
                add(s,(j-)*n+,w);
            else if(i==n)
                add(j*n,t,w);
            else
                add((j-)*n+i,(j-)*n+i+,w);
        }
    }
    /******/
    /***从上到下***/
    for(int i=,w;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            scanf("%d",&w);
            if(j==)
                add(i,t,w);
            else if(j==n)
                add(s,i+n*(n-),w);
            else
                add(j*n+i,(j-)*n+i,w);
        }
    }
    /******/

    /***从右向左***/
    for(int i=,w;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            scanf("%d",&w);
            if(i==)
                add((j-)*n+,s,w);
            else if(i==n)
                add(t,j*n,w);
            else
                add((j-)*n+i+,(j-)*n+i,w);
        }
    }
    /******/

    /***从下到上***/
    for(int i=,w;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            scanf("%d",&w);
            if(j==)
                add(t,i,w);
            else if(j==n)
                add(i+n*(n-),s,w);
            else
                add((j-)*n+i,j*n+i,w);
        }
    }
    /******/
    /*for(int i=1;i<=n*n+2;i++)
    {
        for(int j=head[i];j;j=e[j].next)
            printf("%d=>%d %d\n",i,e[j].to,e[j].w);
    }*///输出建好的图
    /***没啦***/
    printf("%d\n",dijkstra());
    return ;
}