logistic regression model

softmax

classification

Fly

logistic regression model
loss fuction
softmax
基于python的logistic regression代码

logistic regression model

逻辑回归模型一般指的是二项分类的逻辑回归模型，也是非常经典的模型，它主要的决策函数是,给定数据的情况下，来求取Y属于1或者0的概率。具体的，我们可以做如下表示：

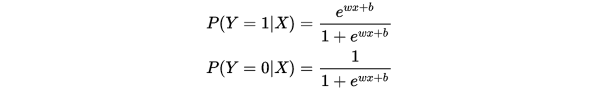
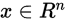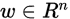这里，是输入，是输出，和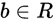是模型参数，是内积。

当然这里的决策函数化简后就是众所周知的sigmoid函数。这里我们使用更为通用的hypothesis来表示函数，具体如下：

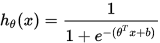
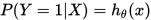
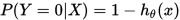
loss fuction

当我们的假设函数确定后，我们就需要来确定真实值与假设函数值之间能量损失。通俗的讲，我们的目标就是要求假设函数的值无限逼近真实值，是的二者的差值达到最小。从而得到最有的参数。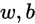

我们可以使用极大似然函数来求解我们的模型参数。0, 1综合起来得到：

求最大似然估计:

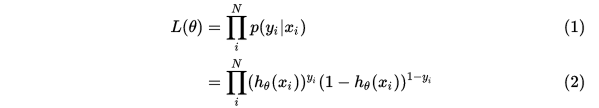
求取对数：

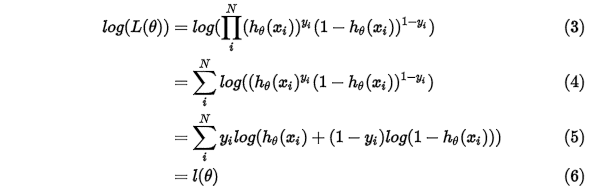
得到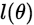之后，我们就可以通过梯度下降法或者牛顿法来求得参数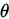，也就是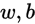

这里我们假设loss function 为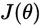可得到：

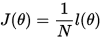
使用梯度下降法来求取模型参数: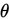

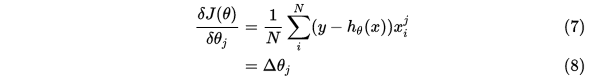
梯度公式更新参数求解：

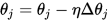
这样子就可以求解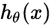的模型参数了。当模型参数确定后就可以用来对数据进行分类了。

softmax

多元逻辑回归，顾名思义就是考虑多分类问题的逻辑回归方法。

它的假设函数为：

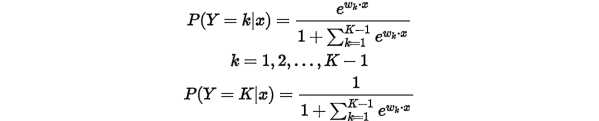
不过这个看着貌似有点繁琐，在Andrew Ng的文章中给出了一个更直观的表现形式：

对于给定的测试输入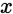,我们想用假设函数针对每一个类别j估算出概率值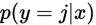。也就是说，我们想估计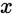的每一种分类结果出现的概率。因此，我们的假设函数将要输出一个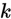维的向量（向量元素的和为1）来表示这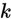个估计的概率值。具体地说，我们的假设函数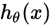形式如下：

这里需要注意的是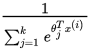这一项对概率分布进行归一化，是的概率之和为1.

具体的代价函数如下：

softmax

以看到，Softmax代价函数与logistic 代价函数在形式上非常类似，只是在Softmax损失函数中对类标记的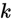个可能值进行了累加。注意在Softmax回归中将分类为类别的概率为：

softmax2

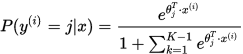
基于python的logistic regression代码

代码来自《机器学习实战》这本书

#!/usr/bin/python

# encoding: utf-8

"""

@version: 1.0

@author: Fly

@license: Apache Licence

@contact: luyfuyu@gmail.com

@site: https://www.flyuuu.cn

@software: PyCharm

@file: logistic_regression.py

"""

import numpy as np

import math

def load_dataset(filename="./data/lr_testSet.txt"):

    data_matrix = []

    label_matrix = []

    with open(filename, 'r') as f:

        for line in f.readlines():

            line_list = line.strip().split()

            data_matrix.append([1.0, float(line_list[0]), float(line_list[1])])

            label_matrix.append(int(line_list[2]))

    return data_matrix, label_matrix

def sigmoid(x):

    return 1/(1 + np.exp(-x))

def grandient_ascent(intput_data, class_labels, maxiter=500):

    data_matrix = np.mat(intput_data)

    label_matrix = np.mat(class_labels).transpose()

    m,n = data_matrix.shape

    alpha = 0.001

    weights = np.ones((n,1))

    for k in range(maxiter):

        h = sigmoid(data_matrix * weights)

        error = label_matrix - h

        weights = weights + alpha * data_matrix.transpose() * error

    return weights

def stoc_ascent(intput_data, class_lables):

    data_matrix = np.mat(intput_data)

    label_matrix = class_lables

    m, n = data_matrix.shape

    alpha = 0.001

    weights = np.ones(n)

    for i in range(m):

        h = sigmoid(data_matrix[i] * weights)

        error = label_matrix[i] - h

        weights = weights + alpha * data_matrix[i] * error

    return weights

def plotBestFit(weights):

    import matplotlib.pyplot as plt

    dataMat, labelMat=load_dataset()

    dataArr = np.array(dataMat)

    n = np.shape(dataArr)[0]

    xcord1 = []

    ycord1 = []

    xcord2 = []

    ycord2 = []

    for i in range(n):

        if int(labelMat[i])== 1:

            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])

        else:

            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])

    fig = plt.figure()

    ax = fig.add_subplot(111)

    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')

    ax.scatter(xcord2, ycord2, s=30, c='green')

    x = np.arange(-3.0, 3.0, 0.1)

    y = ((- weights[0] - weights[1] * x) / weights[2]).tolist()[0]

    ax.plot(x, y)

    plt.xlabel('X1')

    plt.ylabel('X2')

    plt.show()

def stocGradAscent1(dataMatrix, classLabels, numIter=150):

    m,n = np.shape(dataMatrix)

    weights = np.ones(n)   #initialize to all ones

    for j in range(numIter):

        dataIndex = list(range(m))

        for i in range(m):

            alpha = 4/(1.0+j+i)+0.0001    #apha decreases with iteration, does not

            randIndex = int(np.random.uniform(0,len(dataIndex)))#go to 0 because of the constant

            h = sigmoid(sum(dataMatrix[randIndex]*weights))

            error = classLabels[randIndex] - h

            weights = weights + alpha * error * dataMatrix[randIndex]

            del(dataIndex[randIndex])

    return weights

def classifyVector(inX, weights):

    prob = sigmoid(sum(inX*weights))

    if prob > 0.5:

        return 1.0

    else:

        return 0.0

def colicTest():

    frTrain = open('./data/horseColicTraining.txt'); frTest = open('./data/horseColicTest.txt')

    trainingSet = []

    trainingLabels = []

    for line in frTrain.readlines():

        currLine = line.strip().split('\t')

        lineArr =[]

        for i in range(21):

            lineArr.append(float(currLine[i]))

        trainingSet.append(lineArr)

        trainingLabels.append(float(currLine[21]))

    trainWeights = stocGradAscent1(np.array(trainingSet), trainingLabels, 1000)

    errorCount = 0

    numTestVec = 0.0

    for line in frTest.readlines():

        numTestVec += 1.0

        currLine = line.strip().split('\t')

        lineArr =[]

        for i in range(21):

            lineArr.append(float(currLine[i]))

        if int(classifyVector(np.array(lineArr), trainWeights))!= int(currLine[21]):

            errorCount += 1

    errorRate = (float(errorCount)/numTestVec)

    print("the error rate of this test is: %f" % errorRate)

    return errorRate

def multiTest():

    numTests = 10; errorSum=0.0

    for k in range(numTests):

        errorSum += colicTest()

    print ("after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests)))

if __name__ == "__main__":

    filename = "./data/lr_testSet.txt"

    x, y = load_dataset(filename)

    weights = grandient_ascent(x, y)

    plotBestFit(weights)

    multiTest()