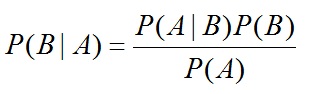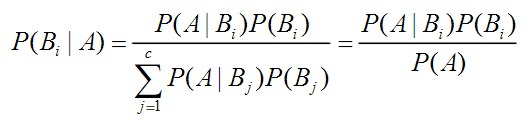OpenCV实现朴素贝叶斯分类器诊断病情
贝叶斯定理由英国数学家托马斯.贝叶斯(Thomas Baves)在1763提出,因此得名贝叶斯定理。贝叶斯定理也称贝叶斯推理,是关于随机事件的条件概率的一则定理。
对于两个事件A和B,事件A发生则B也发生的概率记为P(B|A),事件B发生则A也发生的概率记为P(A|B),这样如果A发生B也必然发生或者B发生A也必然发生,则有P(B|A)=P(A|B)=1,这种情况是一种确定性推理。
更多的情况下,概率推理是不确定性推理,AB之间是一种不确定性概率关系,例如条件A发生时B会发生的概率计算公式为:
这种情况在现实中一般是容易推导计算出来的,或者根据先验知识是可以获取到的,例如如下两种情况:
1.条件A:一个人感冒了;条件B:这个人会发烧
2.条件A:一个人是女生;条件B:这个人会留长发
根据先验知识,条件B发生的概率是可以根据条件A推理得出的。在另一种更普遍的情况下,我们更加关心的是如果条件B发生,那么条件A发生的概率是多少?
1.条件B:一个人发烧了;条件A:这个人感冒了
2.条件B:一个人留长发;条件A:这个人是女生
这个问题称为“逆概率推理”,即已知A发生时B发生的概率,那么如果B已经发生,A发生的概率P(A|B)=?
贝叶斯公式
设有一个样本空间S,划分为B1,B2,....Bc一共c 类,或者成为c个事件,A为引发S中各个事件发生的事件,贝叶斯公式定义为:
其中P(Bi|A)称为后验概率,表示时间A发生后,各不相容的条件Bi发生的概率,它是在A的结果出现之后才能计算的,所以称为后验概率。
P(A|Bj)称为类条件概率,表示在各条件Bi存在时,事件A发生的概率。
P(Bj)称为先验概率,表示各不相容的条件Bi出现的概率,它与结果A是否出现无关,仅表示根据先验知识或者主观推断,认为总体上各个条件出现的可能性之间的差别。
贝叶斯是一位牧师,据不可靠消息,贝叶斯提出贝叶斯公式的目的是为了从统计理论上证明上帝的存在,尝试以一个科学的东西证明一个非科学的东西的科学性,这不科学。
朴素贝叶斯分类器(Naive Baves classifier)的“朴素”(Naive)之处在于,其假设了各个特征之间是独立的,简化了贝叶斯各个特征之间的相互关联,更易于推广应用。
以下代码是使用Opencv中正态贝叶斯Normal BavesClassifier 类建立的一个简单的病情诊断功能。假定以下是根据警院历来可靠数据获取的体温、咳嗽、流涕三个症状的严重程度判定的三类病情,分别是冷感冒、肺炎、热感冒。朴素贝叶斯根据这10组数据进行训练,然后输入一位病人的数据,自动进行诊断,以下是训练数据:
Opencv代码实现:
#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/ml/ml.hpp"
#include <iostream>
using namespace cv;
using namespace std;
int main( int argc, char** argv )
{
float trainingData[10][3] = { {34, 1, 1}, {35, 2, 2}, {36, 3,3},{37,8,4},{38,9,5},
{39,10,6},{40,7,7},{41,4,8},{42,5,9},{43,6,10}};
Mat trainingDataMat(10, 3, CV_32FC1, trainingData);
float responses[10] = {1,1,1,2,2,2,3,3,3};
Mat responsesMat(10, 1, CV_32FC1, responses);
NormalBayesClassifier nbc;
nbc.train(trainingDataMat, responsesMat);
float myData[3] = {40, 8, 10}; //病人发烧、咳嗽、流涕数据
Mat myDataMat(1, 3, CV_32FC1, myData);
float r = nbc.predict( myDataMat );
int result=r;
string output;
switch(result)
{
case 1:
output="冷感冒";
break;
case 2:
output="肺炎";
break;
case 3:
output="热感冒";
break;
default:
output="健康";
break;
}
cout<<endl<<"该病人诊断为: "<<output<<endl<<endl;
system("pause");
return 0;
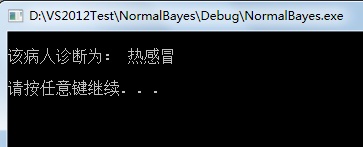
}输入病人的数据为:发烧-40、咳嗽-8、流涕-10,诊断结果为:
OpenCV实现朴素贝叶斯分类器诊断病情的更多相关文章
- 朴素贝叶斯分类器(Naive Bayesian Classifier)
本博客是基于对周志华教授所著的<机器学习>的"第7章 贝叶斯分类器"部分内容的学习笔记. 朴素贝叶斯分类器,顾名思义,是一种分类算法,且借助了贝叶斯定理.另外,它是一种 ...
- 数据挖掘十大经典算法(9) 朴素贝叶斯分类器 Naive Bayes
贝叶斯分类器 贝叶斯分类器的分类原理是通过某对象的先验概率,利用贝叶斯公式计算出其后验概率,即该对象属于某一类的概率,选择具有最大后验概率的类作为该对象所属的类.眼下研究较多的贝叶斯分类器主要有四种, ...
- 用scikit-learn实现朴素贝叶斯分类器 转
原文:http://segmentfault.com/a/1190000002472791 朴素贝叶斯(Naive Bayes Classifier)是一种「天真」的算法(假定所有特征发生概率是独立的 ...
- 十大经典数据挖掘算法(9) 朴素贝叶斯分类器 Naive Bayes
贝叶斯分类器 贝叶斯分类分类原则是一个对象的通过先验概率.贝叶斯后验概率公式后计算,也就是说,该对象属于一类的概率.选择具有最大后验概率的类作为对象的类属.现在更多的研究贝叶斯分类器,有四个,每间:N ...
- 机器学习---朴素贝叶斯分类器(Machine Learning Naive Bayes Classifier)
朴素贝叶斯分类器是一组简单快速的分类算法.网上已经有很多文章介绍,比如这篇写得比较好:https://blog.csdn.net/sinat_36246371/article/details/6014 ...
- 朴素贝叶斯分类器及Python实现
贝叶斯定理 贝叶斯定理是通过对观测值概率分布的主观判断(即先验概率)进行修正的定理,在概率论中具有重要地位. 先验概率分布(边缘概率)是指基于主观判断而非样本分布的概率分布,后验概率(条件概率)是根据 ...
- 朴素贝叶斯分类器(Naive Bayes)
1. 贝叶斯定理 如果有两个事件,事件A和事件B.已知事件A发生的概率为p(A),事件B发生的概率为P(B),事件A发生的前提下.事件B发生的概率为p(B|A),事件B发生的前提下.事件A发生的概率为 ...
- 朴素贝叶斯分类器的应用 Naive Bayes classifier
一.病人分类的例子 让我从一个例子开始讲起,你会看到贝叶斯分类器很好懂,一点都不难. 某个医院早上收了六个门诊病人,如下表. 症状 职业 疾病 打喷嚏 护士 感冒 打喷嚏 农夫 过敏 头痛 建筑工 ...
- PGM学习之三 朴素贝叶斯分类器(Naive Bayes Classifier)
介绍朴素贝叶斯分类器的文章已经很多了.本文的目的是通过基本概念和微小实例的复述,巩固对于朴素贝叶斯分类器的理解. 一 朴素贝叶斯分类器基础回顾 朴素贝叶斯分类器基于贝叶斯定义,特别适用于输入数据维数较 ...
随机推荐
- PHP unlink() 函数(删除文件)
PHP unlink() 函数(删除文件) 一.总结 unlink() 函数删除文件. 1.实例 $file = "test.txt"; if (!unlink($file)) 2 ...
- aspcms产品详情页调取相关产品
产品详情页调用相关产品最常见的应用就是装饰公司网站,设计师页面要求调取设计师做过的案例.aspcms本身有这个功能,但不能完全符合要求,看代码 {aspcms:content sort={aspcms ...
- Canvas基础知识总结之中的一个
canvas的HTML语法: <canvas> Canvas not supported </canvas> 上面这句代码中内容部分所含的文本,这种文本的叫法"后备内 ...
- swift学习第十五天:闭包
闭包 闭包的介绍 闭包和OC中的block非常相似 OC中的block是匿名的函数 Swift中的闭包是一个特殊的函数 block和闭包都经常用于回调 注意:闭包和block一样,第一次使用时可能不习 ...
- Android(Java) 模拟登录知乎并抓取用户信息
前不久.看到一篇文章我用爬虫一天时间"偷了"知乎一百万用户.仅仅为证明PHP是世界上最好的语言,该文章中使用的登录方式是直接复制cookie到代码中,这里呢,我不以爬信息为目的.仅 ...
- 事件处理之二:点击事件监听器的五种写法 分类: H1_ANDROID 2013-09-11 10:32 4262人阅读 评论(1) 收藏
首选方法二! 方法一:写一个内部类,在类中实现点击事件 1.在父类中调用点击事件 bt_dail.setOnClickListener(new MyButtonListener()); 2.创建内部类 ...
- 正确使用pthread_create,防止内存泄漏
近日,听说pthread_create会造成内存泄漏,觉得不可思议,因此对posix(nptl)的线程创建和销毁进行了分析. 分析结果:如果使用不当,确实会造成内存泄漏. 产生根源:pthread ...
- maven打包到本地库
mvn install:install-file -DgroupId=com.alipay -DartifactId=com.alipay.core -Dversion=20180104135026 ...
- php实现表示数值的字符串(is_numeric($s))
php实现表示数值的字符串(is_numeric($s)) 一.总结 is_numeric($s) 二.php实现表示数值的字符串 题目描述 请实现一个函数用来判断字符串是否表示数值(包括整数和小数) ...
- Android 比较两个时间段是否有交集或重复
先看一个例图: 在金山<电池管家>应用中就有一个类似上图这样的功能—— 开启多个定时任务. 当开启另一个定时任务的时候,如果即将开启的这个定时任务的时间段与已经开启了的定时任务的时间段有交 ...