Codeforces 959E. Mahmoud and Ehab and the xor-MST 思路：找规律题，时间复杂度O(log(n))

　　题目：

解题思路

　　

这题就是0,1,2...n-1总共n个数字形成的最小生成树。

我们可以发现，一个数字k与比它小的数字形成的异或值，一定可以取到k与所有正整数形成的异或值的最小值。

要计算n个数字的情况我们可以通过n-1个数字的情况得来，意为前n-1个数字的最小生成树已经生成好了，我们需要给第n个数字连一条边，使新的树为n个数字的最小生成树。

通过找规律我们可以发现：

1. 每隔2个数字多一个权值为1的边。
2. 每隔4个数字多一个权值为2的边。
3. 每隔8个数字多一个权值为4的边。
4. ……
5. 每隔2^n个数字多一个权值为2^(n-1)的边。

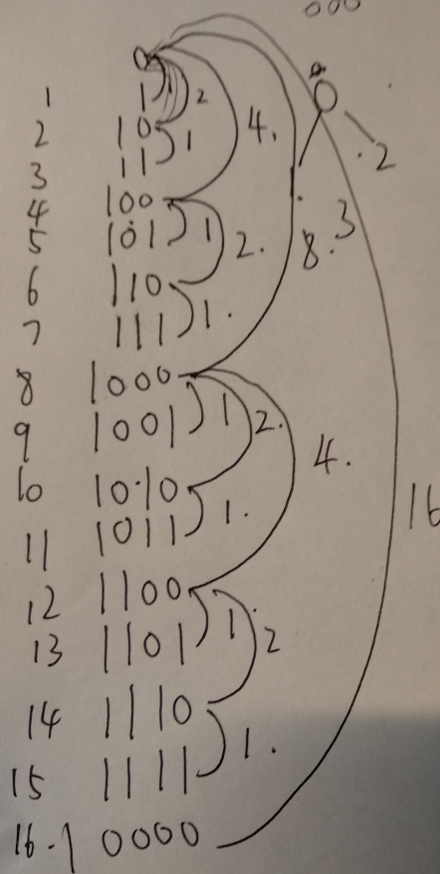
我们把这些边加起来可以推出这样一个公式：

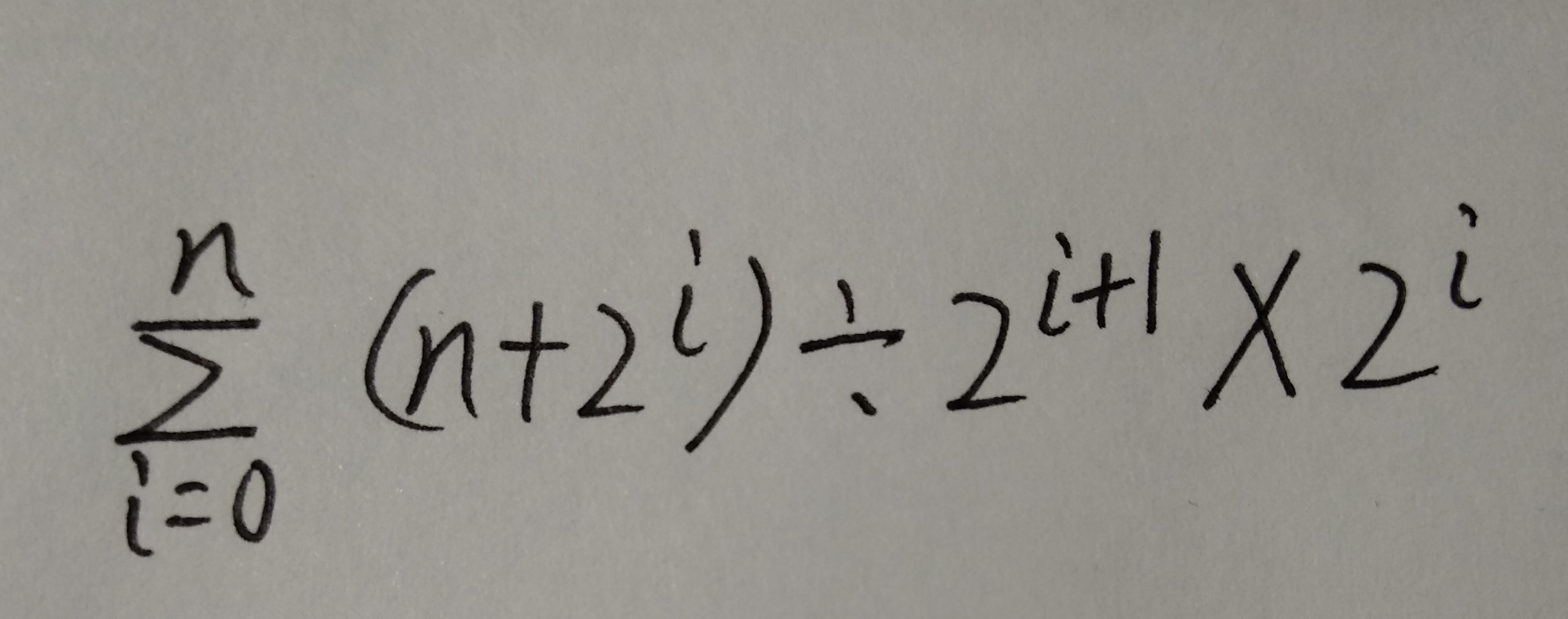
注意除以2^(i+1)和乘2^i不能直接抵消，因为这里的数字全是int型，没有小数。

时间复杂度：

　　O（log（n））

代码：

#include<bits\stdc++.h>
using namespace std;
typedef long long ll;
int main(){
    ll n;
    while(cin >> n){
        n--;
        int m = log(n)/log();
        ll ans = ;
        for(int i = ;i <= m; i++){
            ans += ((ll)(n+pow(,i))/(ll)pow(,i+))*(ll)pow(,i);
        }
        cout << ans << endl;
    }
    return ;
}