【xsy2440】【GDOI2016】疯狂动物城

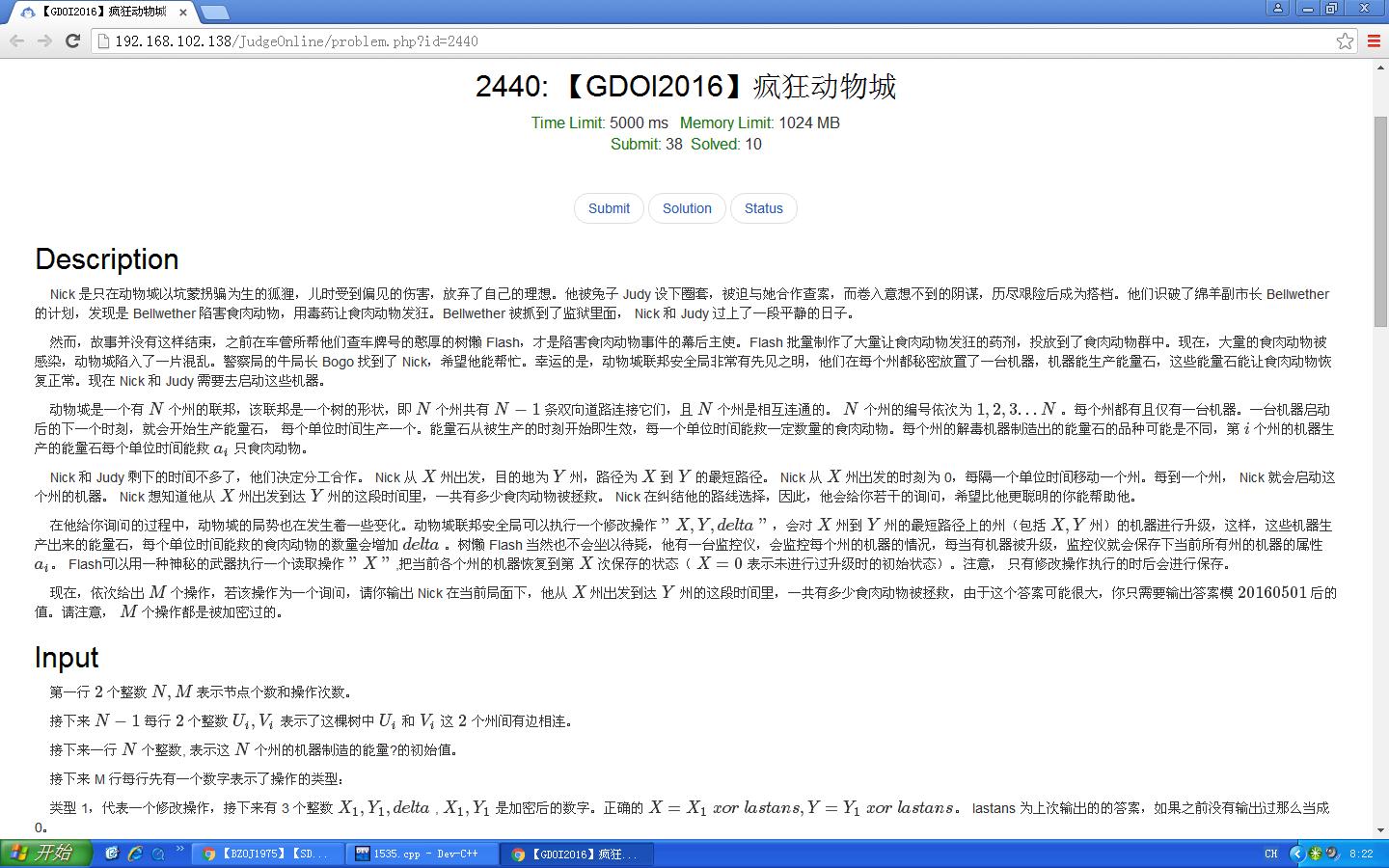
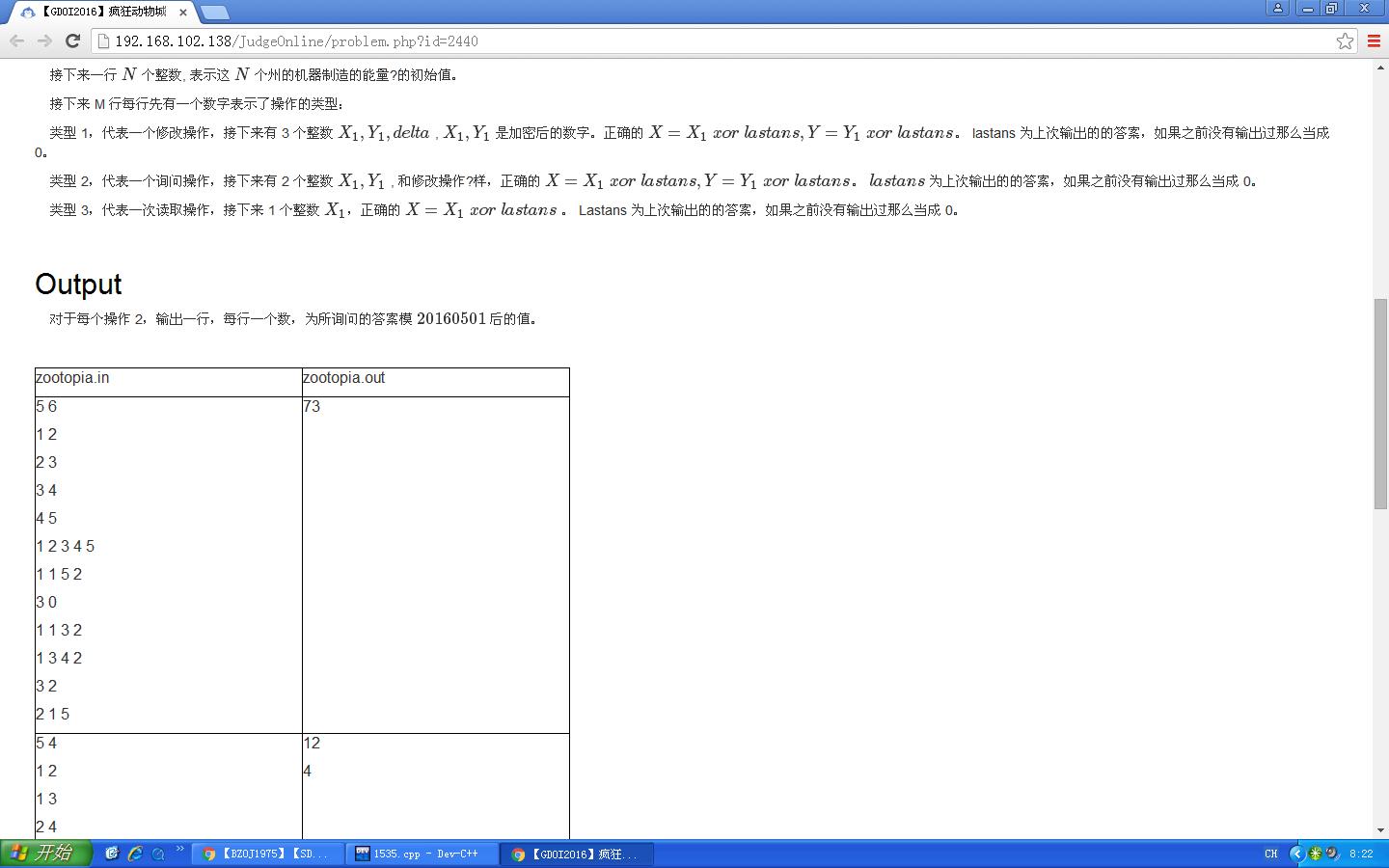
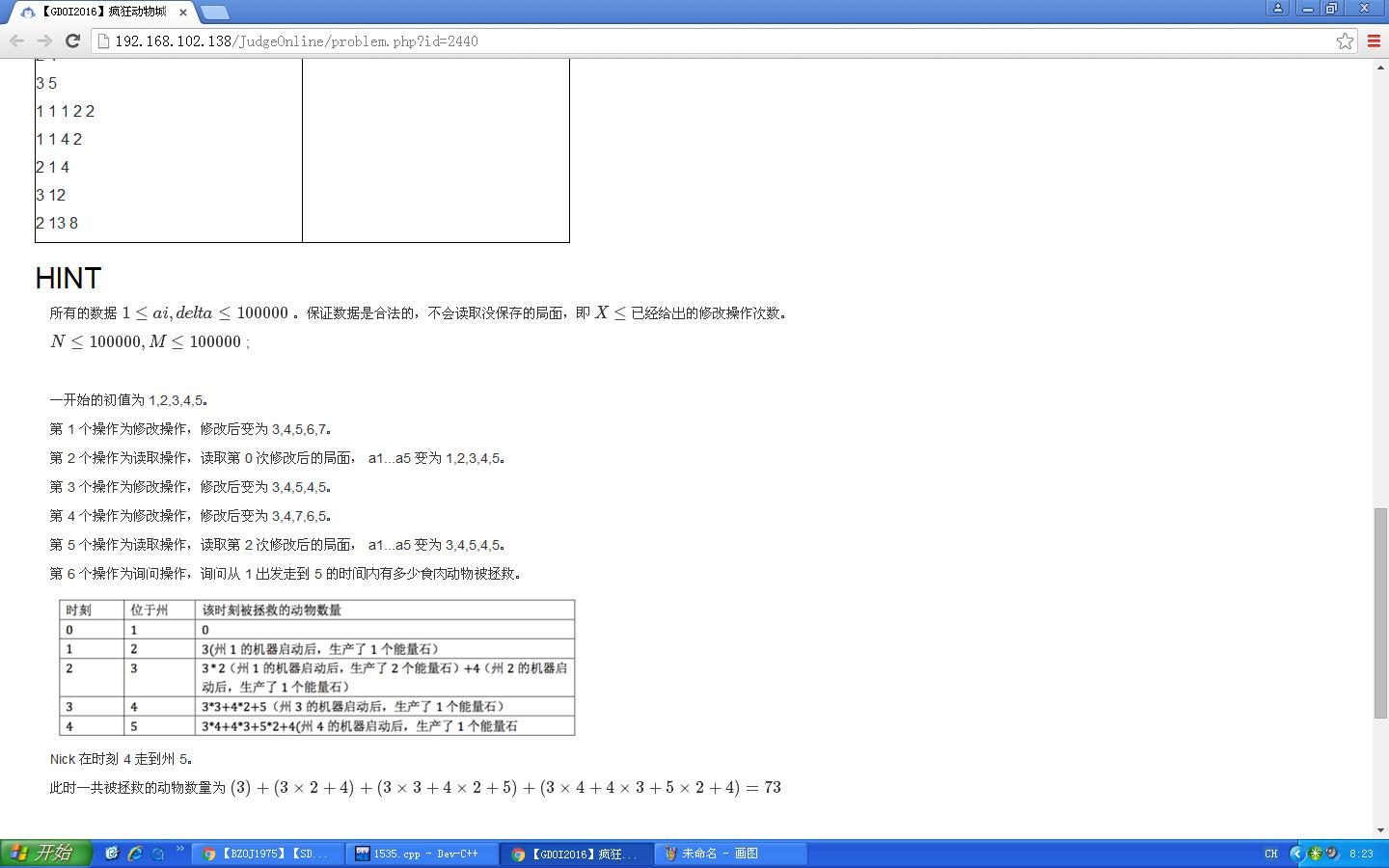
感受一下这恐怖的题目长度~~~

其实题意很裸，但是作为GDOI的一道防AK题，自然有他优秀的地方。

简化题意：给出一棵树，要求支持三个操作：

1.修改点值

2.询问点$x$到$y$之间的一些东东

3.回到某个版本之前

可持久化，强制在线。

考虑拆一下询问

如果把$x$到$y$路径上的所有点值放到一个数组$a$里，那么询问式子就是：

$\sum\limits_{i=1}^{n}a[i]\times\sum\limits_{j=1}^{n-i}j$

$=\sum\limits_{i=1}^{n}a[i]\times\frac{(n-i+1)\times(n-i)}{2}$

$=\sum\limits_{i=1}^{n}a[i]\times i^{2}-a[i]\times(2n+1)+a[i]\times n\times(n+1)$

发现$a[i]$，$a[i]\times i$，$a[i]\times i^2$都是常系数，于是就可以快乐维护了~

外面的很容易想到，树链剖分+可持久化线段树，单点修改即可。

可以感觉到逐渐膨胀的代码量>_<

注意到有左右方向的区别，要写两遍

代码量起飞了>_<

5000B刷新最长代码记录

注意：记得取模，随时爆int；

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #define mod 20160501
 using namespace std;
 typedef long long ll;
 struct edge{
     int v,next;
 }a[];
 struct data{
     ll s,a1,a2,s1,s2,ls,rs,lz,vv;
 }t[];
 ll n,m,u,v,w,ord,tim=,tot=,tote=,ans=,nrt=,nowrt=,last=,ans1[],ans2[],head[],rt[],num[],nmd[],dep[],top[],siz[],dfn[],son[],fa[];
 void add(int u,int v){
     a[++tote].v=v;
     a[tote].next=head[u];
     head[u]=tote;
 }
 void dfs1(int u,int f,int dpt){
     fa[u]=f;
     dep[u]=dpt;
     siz[u]=;
     for(int tmp=head[u];tmp!=-;tmp=a[tmp].next){
         int v=a[tmp].v;
         if(v==f)continue;
         dfs1(v,u,dpt+);
         siz[u]+=siz[v];
         if(son[u]==-||siz[v]>siz[son[u]])son[u]=v;
     }
 }
 void dfs2(int u,int nowtp){
     top[u]=nowtp;
     dfn[u]=++tim;
     nmd[tim]=u;
     if(son[u]==-)return;
     dfs2(son[u],nowtp);
     for(int tmp=head[u];tmp!=-;tmp=a[tmp].next){
         int v=a[tmp].v;
         if(v==son[u]||v==fa[u])continue;
         dfs2(v,v);
     }
 }
 void pushup(int u){
     t[u].s=(t[t[u].ls].s+t[t[u].rs].s)%mod;
     t[u].a1=(t[t[u].ls].a1+t[t[u].rs].a1)%mod;
     t[u].a2=(t[t[u].ls].a2+t[t[u].rs].a2)%mod;
     t[u].s1=(t[t[u].ls].s1+t[t[u].rs].s1)%mod;
     t[u].s2=(t[t[u].ls].s2+t[t[u].rs].s2)%mod;
 }
 void build(int l,int r,int u){
     if(l==r){
         t[u].s=num[nmd[l]];
         t[u].a1=dep[nmd[l]];
         t[u].a2=(t[u].a1*t[u].a1)%mod;
         t[u].s1=(t[u].s*t[u].a1)%mod;
         t[u].s2=(t[u].s*t[u].a2)%mod;
         return;
     }
     int mid=(l+r)/;
     build(l,mid,t[u].ls=++tot);
     build(mid+,r,t[u].rs=++tot);
     pushup(u);
 }
 void updata(int l,int r,int u,int L,int R,int lst,ll v){
     if(u==tot)t[u]=t[lst];
     if(l==L&&r==R){
         t[u].ls=t[lst].ls;
         t[u].rs=t[lst].rs;
         t[u].lz=(t[u].lz+v)%mod;
         t[u].s1=(t[u].s1+t[u].a1*v)%mod;
         t[u].s2=(t[u].s2+t[u].a2*v)%mod;
         t[u].s=(t[u].s+v*(r-l+))%mod;
         t[u].vv=(t[u].vv+v)%mod;
         return;
     }
     int mid=(l+r)/;
     if(R<=mid){
         if(t[u].rs<=last)t[u].rs=t[lst].rs;
         if(t[u].ls<=last)t[u].ls=++tot;
         updata(l,mid,t[u].ls,L,R,t[lst].ls,v);
     }else if(mid<L){
         if(t[u].ls<=last)t[u].ls=t[lst].ls;
         if(t[u].rs<=last)t[u].rs=++tot;
         updata(mid+,r,t[u].rs,L,R,t[lst].rs,v);
     }else{
         if(t[u].ls<=last)t[u].ls=++tot;
         updata(l,mid,t[u].ls,L,mid,t[lst].ls,v);
         if(t[u].rs<=last)t[u].rs=++tot;
         updata(mid+,r,t[u].rs,mid+,R,t[lst].rs,v);
     }
     t[u].s1=(t[t[u].ls].s1+t[t[u].rs].s1+t[u].a1*t[u].vv%mod)%mod;
     t[u].s2=(t[t[u].ls].s2+t[t[u].rs].s2+t[u].a2*t[u].vv%mod)%mod;
     t[u].s=(t[t[u].ls].s+t[t[u].rs].s+t[u].vv*(r-l+)%mod)%mod;
 }
 void getans(int u,int b,ll lz,ll v){
     ans=(ans+t[u].s2+lz*t[u].a2%mod)%mod;
     ans1[b]=(ans1[b]+t[u].s1+t[u].a1*lz%mod)%mod;
     ans2[b]=(ans2[b]+t[u].s+v*lz%mod)%mod;
 }
 void query(int l,int r,int u,int L,int R,int b,ll lz){
     if(!u)return;
     lz+=t[u].vv;
     if(l==L&&r==R){
         lz-=t[u].lz;
         getans(u,b,lz,r-l+);
         return;
     }
     int mid=(l+r)/;
     if(R<=mid)query(l,mid,t[u].ls,L,R,b,lz);
     else if(mid<L)query(mid+,r,t[u].rs,L,R,b,lz);
     else{
         query(l,mid,t[u].ls,L,mid,b,lz);
         query(mid+,r,t[u].rs,mid+,R,b,lz);
     }
 }
 void work(int t,int t1,int u,int v,ll w){
     while(top[u]!=top[v]){
         if(dep[top[u]]<dep[top[v]])swap(u,v);
         updata(,n,rt[t],dfn[top[u]],dfn[u],rt[t1],w);
         u=fa[top[u]];
     }
     if(dep[u]>dep[v])swap(u,v);
     updata(,n,rt[t],dfn[u],dfn[v],rt[t1],w);
 }
 int work1(int t,int u,int v){
     while(top[u]!=top[v]){
         if(dep[top[u]]>dep[top[v]]){
             query(,n,rt[t],dfn[top[u]],dfn[u],,);
             u=fa[top[u]];
         }else{
             query(,n,rt[t],dfn[top[v]],dfn[v],,);
             v=fa[top[v]];
         }
     }
     if(dep[u]>dep[v]){
         query(,n,rt[t],dfn[v],dfn[u],,);
         return v;
     }else{
         query(,n,rt[t],dfn[u],dfn[v],,);
         return u;
     }
 }
 int main(){
     memset(son,-,sizeof(son));
     memset(head,-,sizeof(head));
     scanf("%lld%lld",&n,&m);
     for(int i=;i<n;i++){
         scanf("%lld%lld",&u,&v);
         add(u,v);
         add(v,u);
     }
     for(int i=;i<=n;i++)scanf("%lld",&num[i]);
     dfs1(,,);
     dfs2(,);
     rt[]=tot=;
     build(,n,rt[]);
     for(int i=;i<=m;i++){
         scanf("%lld",&ord);
         if(ord==){
             scanf("%lld%lld%lld",&u,&v,&w);
             u^=ans;
             v^=ans;
             last=tot;
             rt[++nrt]=++tot;
             work(nrt,nowrt,u,v,w);
             nowrt=nrt;
         }else if(ord==){
             scanf("%lld%lld",&u,&v);
             u^=ans;
             v^=ans;
             ans=ans1[]=ans1[]=ans2[]=ans2[]=;
             int t=dep[v]-dep[work1(nowrt,u,v)]*;
             ans=(ans+ans1[]*(t*+)%mod+ans2[]*t%mod*(t+)%mod)%mod;
             ans=(ans-ans1[]*(dep[v]*+)%mod+ans2[]*dep[v]%mod*(dep[v]+)%mod+mod)%mod;
             ans=(ans*)%(ll)mod;
             ans=(ans+mod)%mod;
             printf("%lld\n",ans);
         }else{
             scanf("%lld",&u);
             u^=ans;
             nowrt=u;
         }
     }
     return ;
 }