斜率DP hdu 3507

Problem Description

Zero has an old printer that doesn't work well sometimes. As it is antique, he still like to use it to print articles. But it is too old to work for a long time and it will certainly wear and tear, so Zero use a cost to evaluate this degree.
One day Zero want to print an article which has N words, and each word i has a cost Ci to be printed. Also, Zero know that print k words in one line will cost

M is a const number.
Now Zero want to know the minimum cost in order to arrange the article perfectly.

 

Input

There are many test cases. For each test case, There are two numbers N and M in the first line (0 ≤ n ≤ 500000, 0 ≤ M ≤ 1000). Then, there are N numbers in the next 2 to N + 1 lines. Input are terminated by EOF.

 

Output

A single number, meaning the mininum cost to print the article.

 

Sample Input

5 5 5 9 5 7 5

 

Sample Output

230

 

Author

Xnozero

 

Source

2010 ACM-ICPC Multi-University Training Contest（7）——Host by HIT

大致题意：要打印一长串词语，每个词语有一个对应的打印费用Ci，要给词语分行，一行的总费用记为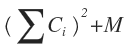,M是给定的常数

要求计算一种分行方案使得总费用最小。

数据规模50万。

分析：首先可以想到枚举上一次断行处，这样可以得到最初的状态转移方程：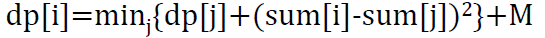

，复杂度为O(n^2)。

观察一下数据规模为50万，需要优化。

主要思路是考虑淘汰肯定对最优答案没有贡献的点。

将状态转移方程展开：

（注：公式和图来自BIG YAO学长）

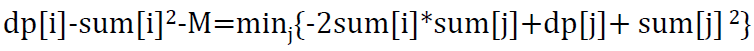
移项可得：

　　　　　　　　　　　　　　　　　　　　

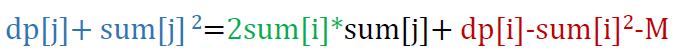
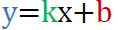
观察到蓝色字体部分只与j有关，绿色字体对给定的i为常量，红色字体部分取最小的时候dp[i]取最小。

将蓝色字体视为y(j),sum[j]视为x(j)，问题就转化为对平面上无数个点（x,y），对每一个i，找出一个最优点（x0,y0），使得一条通过该点，斜率为k=2sum[i]的直线的截距最小。

放张图表现一下优化情况：

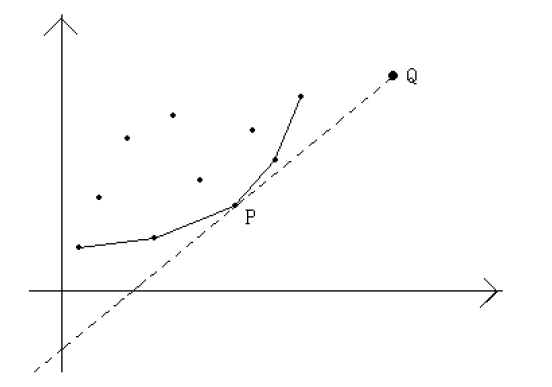
维护一个队列，即为下凸折线上点的队列，每次寻找最优的j的时候只在队列里的点找。（注意取得最优点的时候相邻的两根折线的斜率对于k=2sum[i]一大一小）

以下具体讨论怎么实现：

i不断向前推进，每次循环做两件事情：

1，找出对于dp[i]最优的上一个断行处j

如果队列上该点i和他后面的那个店形成的斜率小于k=2*sum[i]就头指针+1。

注意由于随i的递增，k=2*sum[i]必然递增，所以出队的点就不需要回来了

2，把i放入队列后就不再需要的点淘汰掉：

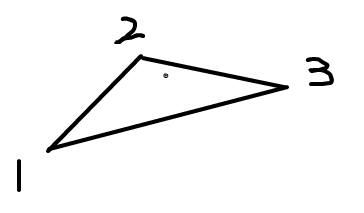
一旦出现3个点呈这样，即可淘汰点2，因为：直线经过点4的截距必然小于经过点2的截距，而经过点4的截距必然小于经过点1或点3的截距。

从而经过点2的截距必然小于小1或点3的截距，点2不可能为最优点，可淘汰。

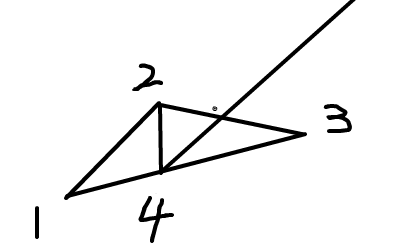
然后把i放入队列（注意sum[i]为严格递增的，所以i个点中最后一个点必然在“外围”，不会被淘汰）

 #include<cstdio>
 #include<algorithm>
 #define rep(i,a,b) for(int i=a;i<=b;++i)
 using namespace std;
 const int MAXN=;
 long long int dp[MAXN],q[MAXN],sum[MAXN];
 int n,m;
 inline long long int getdp(int i,int j)
 {
     return dp[j]+m+(sum[i]-sum[j])*(sum[i]-sum[j]);
 }
 inline long long int gety(int x,int y)
 {
     return dp[x]+sum[x]*sum[x]-dp[y]-sum[y]*sum[y];
 }
 inline long long int getx(int x,int y)
 {
     return *sum[x]-*sum[y];
 }
 int main()
 {
    // freopen("in.txt","r",stdin);
     while(scanf("%d%d",&n,&m)==)
     {
         sum[]=;
         rep(i,,n)
         {
             scanf("%lld",&sum[i]);
             sum[i]=sum[i-]+sum[i];
         }
         dp[]=;
         int head,tail;
         tail=;
         head=;
         q[tail]=;          //虚拟制造一个点0，若0点最优代表把所有词语分成一行最优
         rep(i,,n)
         {
             while(head+<=tail&&(gety(q[head+],q[head])<=sum[i]*getx(q[head+],q[head]))) head++;  //寻找对于i最好的上一次分行的截止点
             dp[i]=getdp(i,q[head]);
             while(head+<=tail&&gety(i,q[tail])*getx(q[tail],q[tail-])<=gety(q[tail],q[tail-])*getx(i,q[tail])) tail--;      //i放入队列后需要淘汰的点
             q[++tail]=i;        //把i放入队列
         }
         printf("%lld\n",dp[n]);
     }
     return ;
 }