【算法】二叉查找树实现字典API
二叉查找树的定义


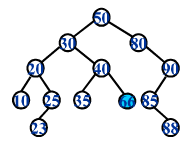

一颗二叉查找树对应一个有序序列
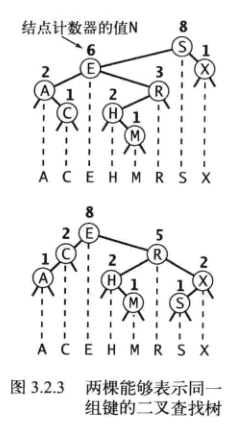

本文的字典API
int size() 获取字典中键值对的总数量
void put(int key, int val) 将键值对存入字典中
int get(int key) 获取键key对应的值
void delete(int key) 从字典中删去对应键(以及对应的值)
int min() 字典中最小的键
int max() 字典中最大的键
int rank(int key) key在键中的排名(小于key的键的数量)
int select(int k) 获取排名为k的键
BST类的基本结构
public class BST {
Node root; // 根结点
private class Node { // 匿名内部类Node
int key; // 存储字典的键
int val; // 存储字典的值
Node left,right; // 分别表示左链接和右链接
int N; // 以该结点为根的子树中的结点总数
public Node (int key,int val,int N) {
this.key = key;
this.val = val;
this.N = N;
}
}
public int get (int key) { }
public void put (int key,int val) { }
// 其他方法 ... ...
}
Node内部类中成员变量N的作用


- 如果你不需要rank/select方法, 那么N完全可以设为BST的成员变量, 表示的是整棵树的结点总数, 维护N的代码编写很简单:在调用put方法时候使其加1, 在调用delete方法时使其减1。
- 如果你需要rank/select方法,则需对每个结点单独设N,代表的是该结点为根的子树中的结点总数,维护N的代码编写将会复杂很多,但这是必要的。(具体往下看)
方法设计的共同点
// 针对某个结点设计的递归处理方法
private int get(Node x, int key) {
// 递归调用get方法
}
// 将root作为上面方法的参数,从根结点开始处理整颗二叉树
public int get(int key) {
return get(root, key)
}
size方法
private int size (Node x) {
if(x == null) return 0;
return x.N;
}
public int size () {
return size(root);
}
- 当结点存在的时候,返回结点所在子树的结点总数(包括自身)
- 当结点不存在的时候,即x为null时,返回0
get方法
- key小于当前结点的键,说明key在左子树,向左儿子递归调用get
- key大于当前结点的键,说明key在右子树,向右儿子递归调用get
- key等于当前结点的键,查找成功并返回对应的值
- 查找到给定的key,返回对应的值
- x迭代至最下方的结点也没有查找到key,因为x.left=x.right=null,在下一次调用get返回-1,结束递归
private int get (Node x,int key) {
if(x == null) return -1; // 结点为空, 未查找到
if(key<x.key) {
return get(x.left,key); // 键在左子树,向左子树查找
}else if(key>x.key) {
return get(x.right, key); // 键在右子树,向右子树查找
}else{
return x.val; // 查找成功,返回值
}
}
public int get (int key) {
return get(root,key);
}

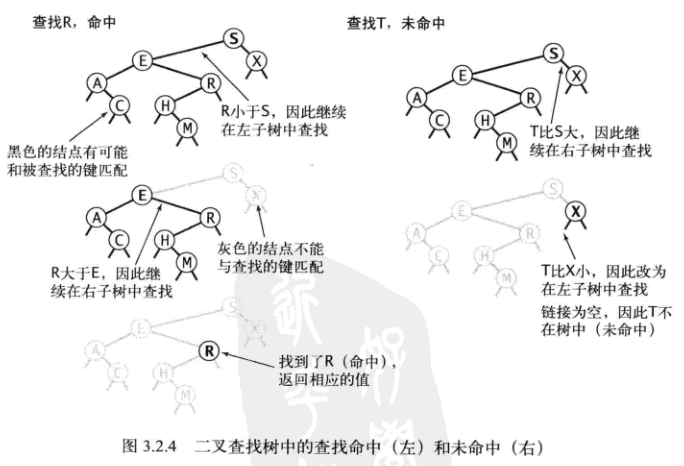
put方法
- key小于当前结点的键,向左子树插入
- key大于当前结点的键,向右子树插入
- key等于当前结点的键,则将值替换为给定的val
private Node put (Node x, int key, int val) {
if(x == null) return new Node(key,val,1); // 未查找到key,创建新结点,并插入树中
if(key<x.key){
x.left = put(x.left,key,val); // 向左子树插入
}else if(key>x.key){
x.right = put(x.right,key,val); // 向右子树插入
}else {
x.val = val; // 查找到给定key, 更新对应val
}
x.N =size(x.left) + size(x.right) + 1; // 更新结点计数器
return x; //
}
public void put (int key,int val) {
if(root == null) root = put(root,key,val); // 向空树中插入第一个结点
put(root,key,val);
}


x.N =size(x.left) + size(x.right) + 1; // 更新结点计数器
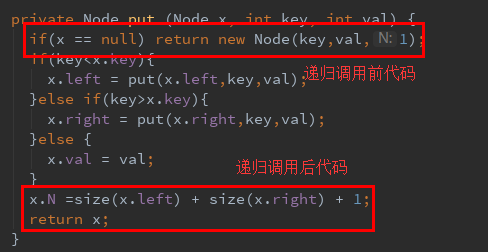

- 递归调用前代码先执行, 而递归调用后代码后执行
- 递归调用前代码是一个“沿着树向下走”的过程,即递归层次是由浅到深, 而递归调用后代码是一个“沿着树向上爬”的过程, 即递归层次是由深到浅
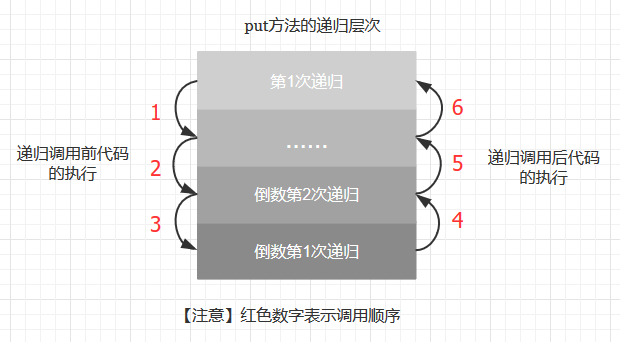


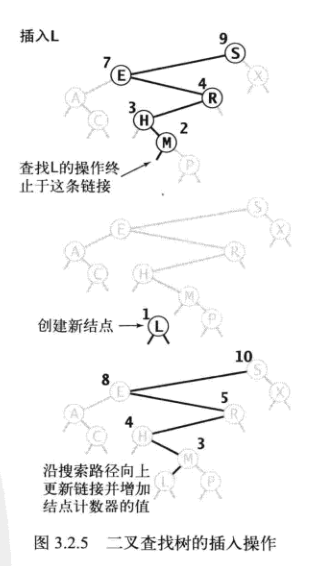
- 先“沿着树向下走”, 插入或更新结点
- 再“沿着树向上爬”, 更新结点计数器N
min,max方法

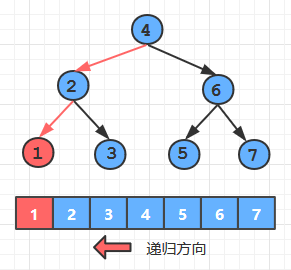
private Node min (Node x) {
if(x.left == null) return x; // 如果左儿子为空,则当前结点键为最小值,返回
return min(x.left); // 如果左儿子不为空,则继续向左递归
}
public int min () {
if(root == null) return -1;
return min(root).key;
}
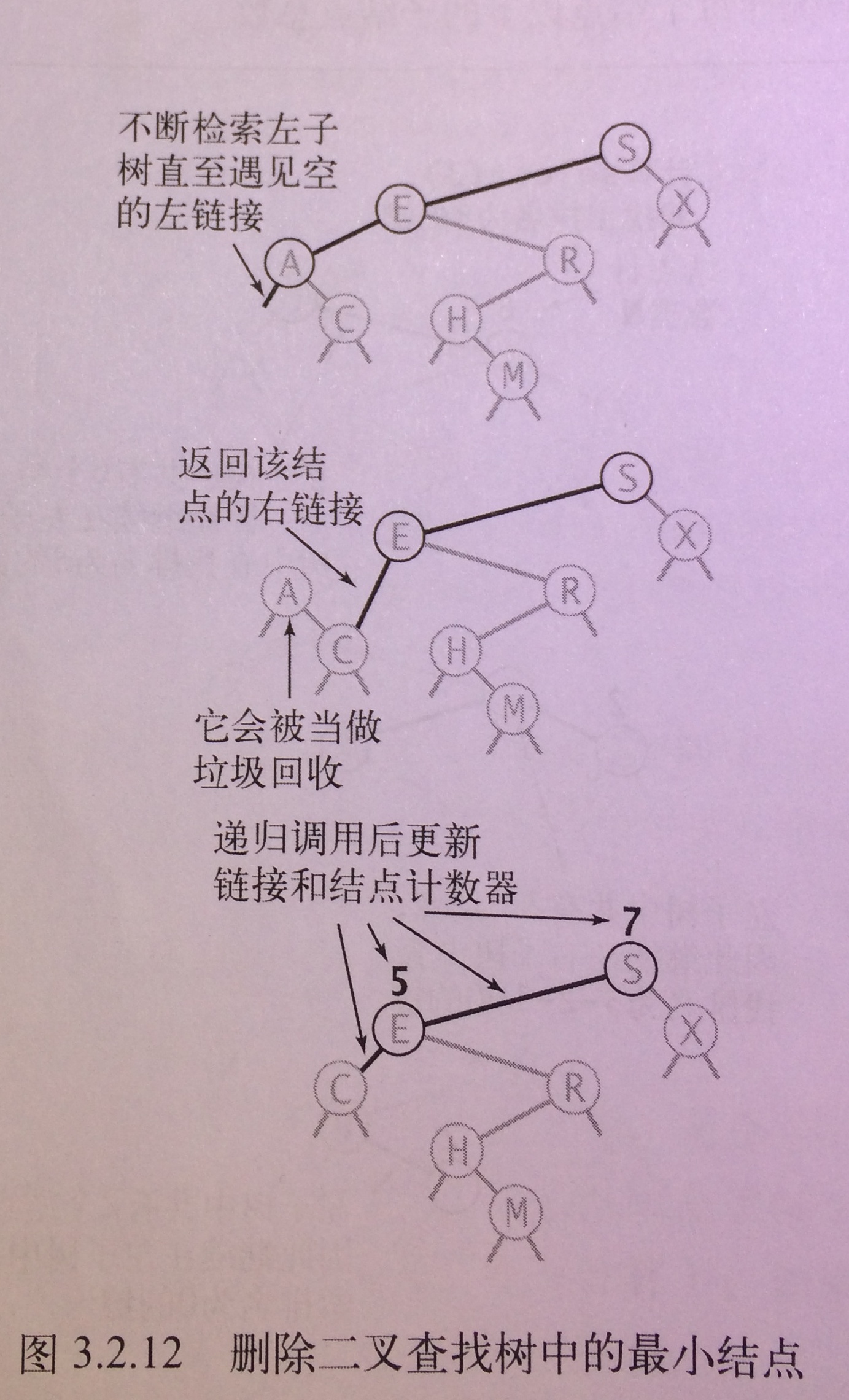
deleteMin方法
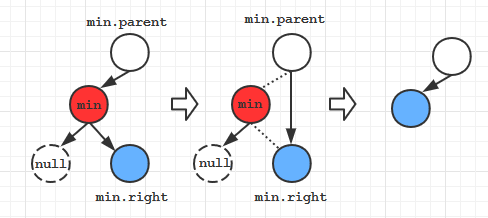

public Node deleteMin (Node x) {
if(x.left==null) return x.right; // 如果当前结点左儿子空,则将右儿子返回给上一层递归的x.left
x.left = deleteMin(x.left);// 向左子树递归, 同时重置搜索路径上每个父结点指向左儿子的链接
x.N = size(x.left) + size(x.right) + 1; // 更新结点计数器N
return x; // 当前结点不是min ###
}
public void deleteMin () {
root = deleteMin(root);
}
- 沿搜索路径重置结点链接
- 更新路径上的结点计数器
- 在递归到最后一个结点前, 下一层递归返回值是x(代码中###处), 这时,对上一层递归来说, x.left = deleteMin(x.left)等同于x.left = x.left
- 当递归到最后一个结点时,下一层递归中x = min, x.left==null判定为true, 返回x.right给上一层递归, 对上一层递归来说,x.left = deleteMin(x.left)等同于x.left = x.left.right;

delete方法






- 相对于父节点(A)而言是有序的。
- 相对于左子树(B)而言是有序的(15原本位于14右子树,所以大于14的左子树)
- 相对于右子树(C)而言是有序的(15是原来14右子树的最小键,移动后也小于C中其他结点)
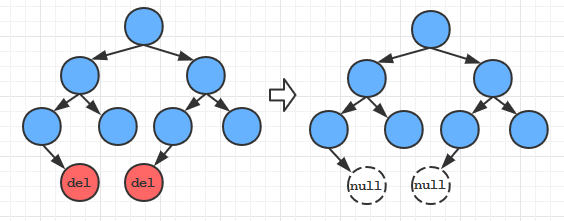
- 查找到相应的结点
- 将其删除






public Node delete (int key,Node x) {
if(x == null) return null;
if(key<x.key){
x.left = delete(key,x.left); // 向左子树查找键为key的结点 #1
}else if (key>x.key){
x.right = delete(key,x.right); // 向右子树查找键为key的结点 #2
}else{ // 在这个else里结点已经被找到,就是当前的x
// 这里处理的是上述的 第一种情况和第二种情况:左子树为null或右子树为null(或都为null)
if(x.left==null) return x.right; // 如果左子树为空,则将右子树赋给父节点的链接 #3
if(x.right==null) return x.left; // 如果右子树为空,则将左子树赋给父节点的链接 #4
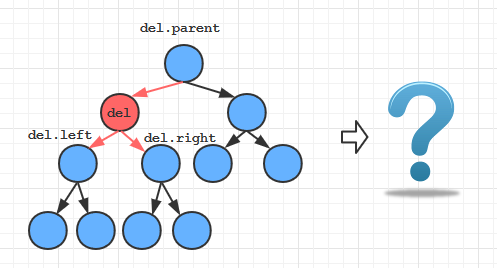
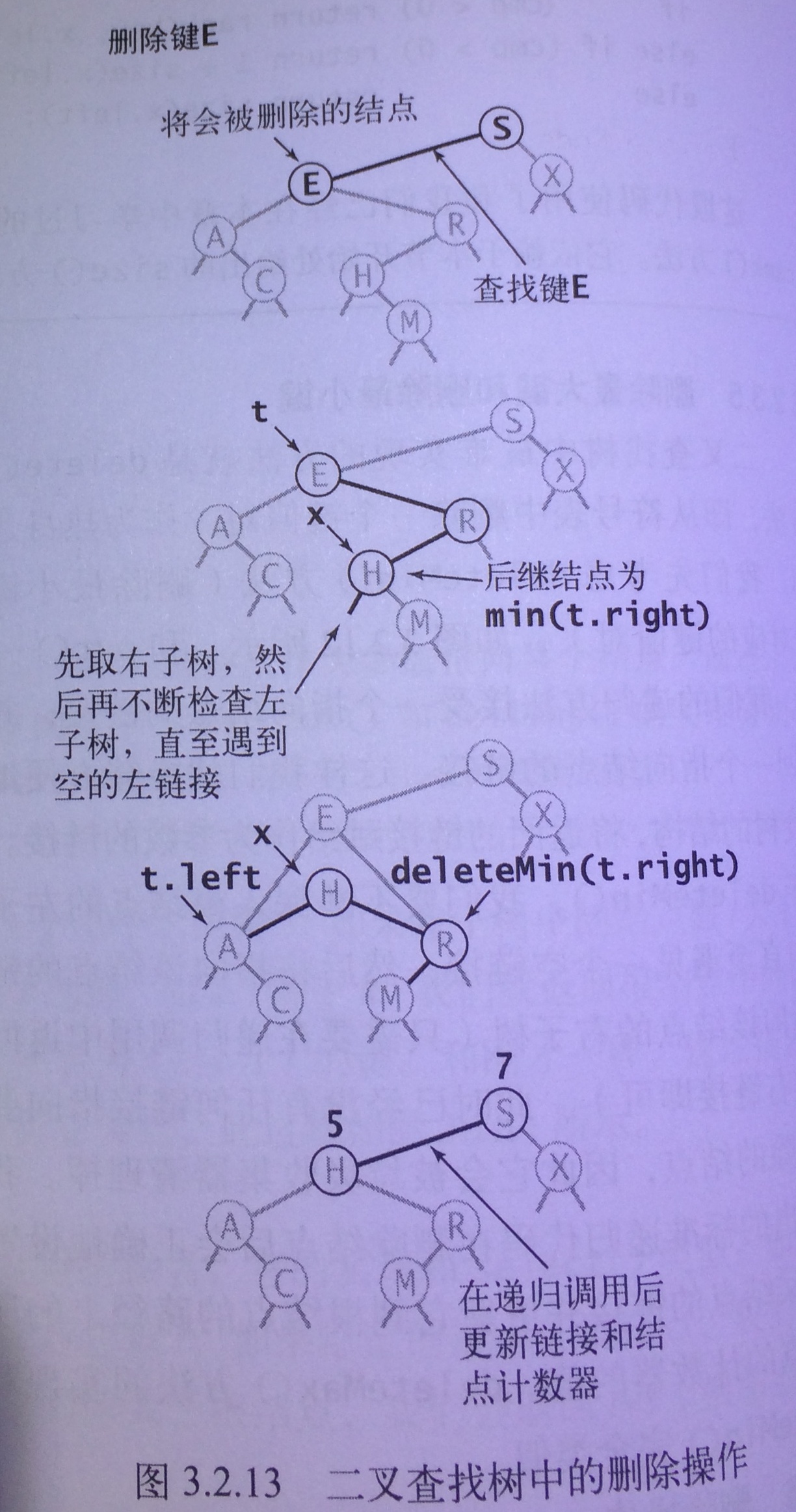
// 这里处理的是上述的第三种情况
Node inherit = min(x.right); // 取得结点x的继承结点
inherit.right = deleteMin(x.right); // 将继承结点从原来位置删除,并重置继承结点右链接
inherit.left = x.left; // 重置继承结点左链接
x = inherit; // 将x替换为继承结点
}
x.N = size(x.left)+ size(x.right) + 1; // 更新结点计数器
return x; // #5
}
public void delete (int key) {
root = delete(key, root);
}

rank方法



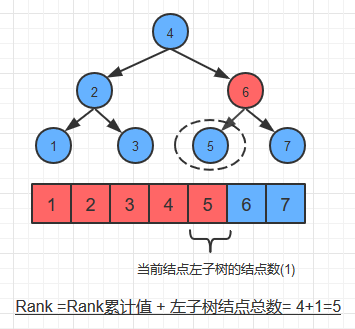
public int rank (Node x,int key) {
if(x == null) return 0;
if(key<x.key) {
return rank(x.left,key);
}else if(key>x.key) {
return size(x.left) + 1 + rank(x.right, key);
}else {
return size(x.left);
}
}
public int rank (int key) {
return rank(root,key);
}
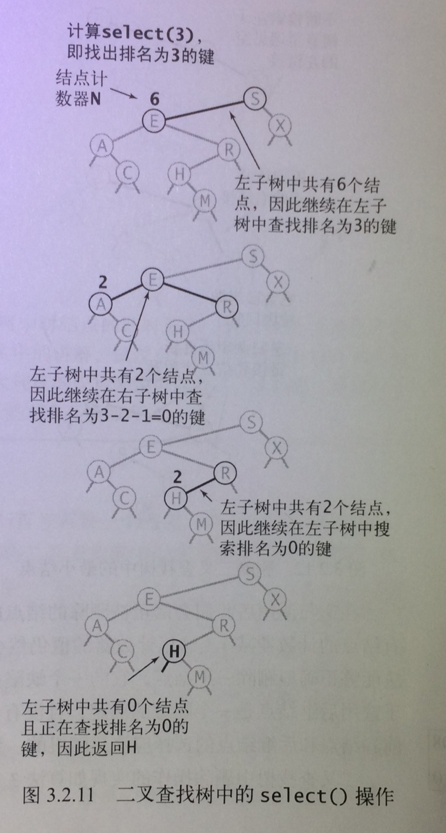
select方法
private Node select (Node x,int k) {
if(x==null) return null;
int t = size(x.left);
if(t>k){
return select(x.left,k);
}else if(t<k) {
return select(x.right,k-t-1);
}else {
return x;
}
}
public int select (int k) {
return select(root,k).key;
}
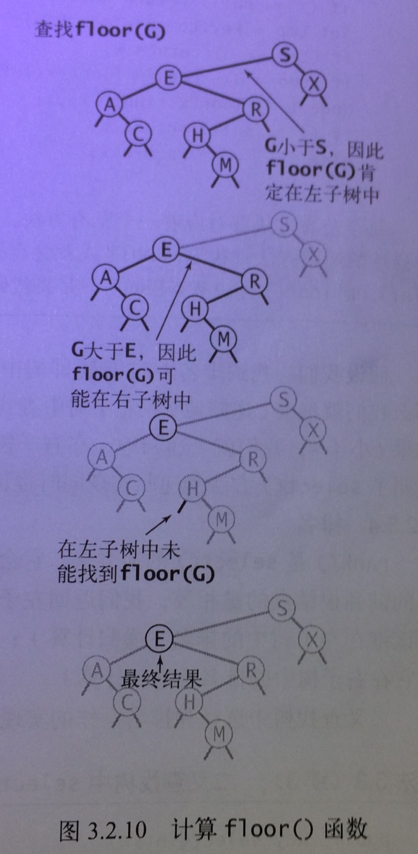
floor、ceiling方法
- 如果递归返回null,说明右子树没有floor值,所以floor值就是当前结点的键,
- 如果递归不为null,说明右子树还有比当前结点键更大的floor值,所以返回递归后的非null的floor值
private Node floor (Node x,int key) {
if(x==null) return null;
if(key<x.key){ // key小于当前结点的键
return floor(x.left,key); // key的floor值在左子树,向左递归
}else if(key==x.key) {
return x; // 和key相等,也是floor值,返回
}else { // 这里排除floor值在左子树,剩下两种可能:floor值是当前结点或在右子树
Node n = floor(x.right, key);
if(n==null) return x; // 右子树没有找到floor值,所以当前结点键就是floor
else return n; // 右子树找到floor值,返回找到的floor值
}
}
public int floor (int key) {
if(root==null) return -1; //树为空, 没有floor值
return floor(root, key).key;
}

【算法】二叉查找树实现字典API的更多相关文章
- 【算法】实现字典API:有序数组和无序链表
参考资料 <算法(java)> — — Robert Sedgewick, Kevin Wayne <数据结构> ...
- 【算法】二叉查找树(BST)实现字典API
参考资料 <算法(java)> — — Robert Sedgewick, Kevin Wayne <数据结构> ...
- 数据结构和算法(Golang实现)(27)查找算法-二叉查找树
二叉查找树 二叉查找树,又叫二叉排序树,二叉搜索树,是一种有特定规则的二叉树,定义如下: 它是一颗二叉树,或者是空树. 左子树所有节点的值都小于它的根节点,右子树所有节点的值都大于它的根节点. 左右子 ...
- Pythoncookbook(数据结构与算法)在字典中将键映射到多个值上的方法
Python cookbook(数据结构与算法)在字典中将键映射到多个值上的方法 本文实例讲述了Python在字典中将键映射到多个值上的方法.分享给大家供大家参考,具体如下: 问题:一个能将键(key ...
- 萌新笔记——用KMP算法与Trie字典树实现屏蔽敏感词(UTF-8编码)
前几天写好了字典,又刚好重温了KMP算法,恰逢遇到朋友吐槽最近被和谐的词越来越多了,于是突发奇想,想要自己实现一下敏感词屏蔽. 基本敏感词的屏蔽说起来很简单,只要把字符串中的敏感词替换成"* ...
- 用KMP算法与Trie字典树实现屏蔽敏感词(UTF-8编码)
前几天写好了字典,又刚好重温了KMP算法,恰逢遇到朋友吐槽最近被和谐的词越来越多了,于是突发奇想,想要自己实现一下敏感词屏蔽. 基本敏感词的屏蔽说起来很简单,只要把字符串中的敏感词替换成“***”就可 ...
- 算法总结篇---字典树(Trie)
目录 写在前面 具体实现 引例: 引例代码: 例题 Phone List Solution: The XOR Largest Pair Solution L语言 Solution: 写在前面 字典树是 ...
- 数据结构和算法 – 6.构建字典: DictionaryBase 类和 SortedList 类
6.1.DictionaryBase 类的基础方法和属性 大家可以把字典数据结构看成是一种计算机化的词典.要查找的词就是关键字,而词的定义就是值. DictionaryBase 类是一种用作专有字 ...
- 【算法】字典的诞生:有序数组 PK 无序链表
参考资料 <算法(java)> — — Robert Sedgewick, Kevin Wayne <数据结构> ...
随机推荐
- myeclipse自动保存修改代码
当你修改过代码后,myeclipse往往要你手动的保存代码才能运行这个修改后的代码,要是不保存就会一直运行修改前的代码.只要修改myeclipse中这两项,就可以让它编译运行修改后的代码: Windo ...
- ASP.NET Core的身份认证框架IdentityServer4(5)- 包和构建
包和构建 IdentityServer有许多nuget包 IdentityServer4 nuget | github 包含IdentityServer核心对象模型,服务和中间件. 仅支持内存配置和用 ...
- 一场围绕着‘Deeping Learning’的高考
Deep Learning的基本思想和方法 实际生活中,人们为了解决一个问题,如对象的分类(对象可是是文档.图像等),首先必须做的事情是如何来表达一个对象,即必须抽取一些特征来表示一个对象,如文本的处 ...
- JDBC+Servlet+jsp(增删查改)
先在mysql新增数据库和表先,把下面的几句代码复制去到mysql运行就可以创建成功了! 创建数据库 create database jdbc01 character set utf8 collat ...
- 使用weinre远程调试
1.调试环境: 1)使用nodejs搭建调试服务器: 先安装node,然后使用npm安装weinre,在node.js安装目录输入以下命令 npm install weinre 2)需要wifi环境和 ...
- ligerUI---ligerGrid中treegrid(表格树)的使用
写在前面: 表格树是在普通ligerGrid的基础上,做了一点改变,使数据以表格树的形式显示出来,适用于有级别的数据比如菜单(有父菜单,父菜单下面有子菜单).表格树的显示有两种方法,可以根据自己的项目 ...
- jQuery选择器(添加节点及删除节点及克隆及替换及包装)第九节
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- iOS字符串修改及运用
//创建字符串 直接赋值 NSString *lytTest = @"A common string"; 1.获取字符串的长度 NSLog(@"%d",lytT ...
- 高效sql2005分页存储过程
高效分页存储过程 --分页存储过程示例 Alter PROCEDURE [dbo].[JH_PageDemo] @pageSize int = 9000000000, @pageIndex int = ...
- 【转】Entity Framework 5.0系列之自动生成Code First代码
在前面的文章中我们提到Entity Framework的“Code First”模式也同样可以基于现有数据库进行开发.今天就让我们一起看一下使用Entity Framework Power Tools ...
