[补档]Password

Password

题目

Rivest是密码学专家。近日他正在研究一种数列E = {E[1],E[2],……,E[n]}，且E[1] = E[2] = p（p为一个质数），E[i] = E[i-2]×E[i-1] （若2<i<=n）。

例如{2,2,4,8,32,256,8192,……}就是p = 2的数列。在此基础上他又设计了一种加密算法，该算法可以通过一个密钥q (q < p)将一个正整数n加密成另外一个正整数d，计算公式为：d = E[n] mod q。现在Rivest想对一组数据进行加密，但他对程序设计不太感兴趣，请你帮助他设计一个数据加密程序。

INPUT

第一行读入m，p。其中m表示数据个数，p用来生成数列E。 以下有m行，每行有2个整数n，q。n为待加密数据，q为密钥。 数据范围: 0 < p n< 2^31 0 < q < p 0 < m <= 5000。

OUTPUT

将加密后的数据按顺序输出到文件 第i行输出第i个加密后的数据。

SAMPLE

INPUT1

2 7

4 5

4 6

OUTPUT1

3

1

INPUT2

4 7

2 4

7 1

6 5

9 3

OUTPUT2

3

0

1

1

解题报告

考试时候本以为推了个正解，又强行推出了实现，结果= =

还不如打个暴力

正解：

首先写个公式：

其中，phi(p)为p的欧拉函数。

不要问我怎么证，我不会

然后，我们可以得出，要求的显然就是p^fib(i)%q,其中fib(i)为斐波那契数列的第i项。

显然，正经递推斐波那契是会T的。所以我们考虑优化，显然可以用矩阵快速幂解决问题。

那么，剩下的就很简单了。直接快速幂就可以解决了。

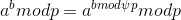
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 using namespace std;
 typedef long long L;
 inline int read(){
     int sum();
     char ch(getchar());
     for(;ch<''||ch>'';ch=getchar());
     for(;ch>=''&&ch<='';sum=sum*+(ch^),ch=getchar());
     return sum;
 }
 L m,p,n,q;
 L fib;
 L unit[][],start[][];
 inline void multi(L a[][],L b[][],L mod){
     L tmp[][]={};
     for(int i=;i<;i++)
         for(int j=;j<;j++)
             for(int k=;k<;k++)
                 tmp[i][j]=(tmp[i][j]+a[i][k]*b[k][j])%mod;
     for(int i=;i<;i++)
         for(int j=;j<;j++)
             b[i][j]=tmp[i][j];
 }
 inline int get_phi(L x){
     L ret(x);
     for(int i=;i*i<=x;i++)
         if(x%i==){
             ret=ret-ret/i;
             while(x%i==)
                 x/=i;
         }
     if(x>)
         ret=ret-ret/x;
     return ret;
 }
 inline L fi(L p,L mod){
 /*  if(p==0)
         return 0;
     if(p==1||p==2)
         return 1;*/
     start[][]=start[][]=start[][]=,start[][]=;
     unit[][]=unit[][]=,unit[][]=unit[][]=;
     while(p){
         if(p&)
             multi(start,unit,mod);
         multi(start,start,mod);
         p>>=;
     }
     return unit[][];
 }
 L mod;
 inline L qpow(L a,L p,L mod){
     L ret();
     while(p){
         if(p&)
             ret*=a,ret%=mod;
         a*=a,a%=mod;
         p>>=;
     }
     return ret;
 }
 int main(){
 //  freopen("1.in","r",stdin);
 //  freopen("1.out","w",stdout);
     m=read(),p=read();
     while(m--){
         n=read(),q=read();
         mod=get_phi(q);
         fib=fi(n,mod);
         fib%=mod;
         printf("%lld\n",qpow(p,fib,q)%q);
     }
 }