Slim Span（Kruskal）

题目链接：http://poj.org/problem?id=3522

 

Slim Span

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 7227		Accepted: 3831

Description

Given an undirected weighted graph G, you should find one of spanning trees specified as follows.

The graph G is an ordered pair (V, E), where V is a set of vertices {v₁, v₂, …, v_n} and E is a set of undirected edges {e₁, e₂, …, e_m}. Each edge e ∈E has its weight w(e).

A spanning tree T is a tree (a connected subgraph without cycles) which connects all the n vertices with n − 1 edges. The slimness of a spanning tree Tis defined as the difference between the largest weight and the smallest weight among the n − 1 edges of T.

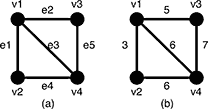
Figure 5: A graph G and the weights of the edges

For example, a graph G in Figure 5(a) has four vertices {v₁, v₂, v₃, v₄} and five undirected edges {e₁, e₂, e₃, e₄, e₅}. The weights of the edges arew(e₁) = 3, w(e₂) = 5, w(e₃) = 6, w(e₄) = 6, w(e₅) = 7 as shown in Figure 5(b).

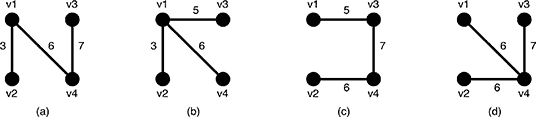
Figure 6: Examples of the spanning trees of G

There are several spanning trees for G. Four of them are depicted in Figure 6(a)~(d). The spanning tree T_a in Figure 6(a) has three edges whose weights are 3, 6 and 7. The largest weight is 7 and the smallest weight is 3 so that the slimness of the tree T_a is 4. The slimnesses of spanning trees T_b,T_c and T_d shown in Figure 6(b), (c) and (d) are 3, 2 and 1, respectively. You can easily see the slimness of any other spanning tree is greater than or equal to 1, thus the spanning tree Td in Figure 6(d) is one of the slimmest spanning trees whose slimness is 1.

Your job is to write a program that computes the smallest slimness.

Input

The input consists of multiple datasets, followed by a line containing two zeros separated by a space. Each dataset has the following format.

n	m
a1	b1	w1
	⋮
am	bm	wm

Every input item in a dataset is a non-negative integer. Items in a line are separated by a space. n is the number of the vertices and m the number of the edges. You can assume 2 ≤ n ≤ 100 and 0 ≤ m ≤ n(n − 1)/2. a_k and b_k (k = 1, …, m) are positive integers less than or equal to n, which represent the two vertices v_ak and v_bk connected by the kth edge e_k. w_k is a positive integer less than or equal to 10000, which indicates the weight of e_k. You can assume that the graph G = (V, E) is simple, that is, there are no self-loops (that connect the same vertex) nor parallel edges (that are two or more edges whose both ends are the same two vertices).

Output

For each dataset, if the graph has spanning trees, the smallest slimness among them should be printed. Otherwise, −1 should be printed. An output should not contain extra characters.

Sample Input

4 5
1 2 3
1 3 5
1 4 6
2 4 6
3 4 7
4 6
1 2 10
1 3 100
1 4 90
2 3 20
2 4 80
3 4 40
2 1
1 2 1
3 0
3 1
1 2 1
3 3
1 2 2
2 3 5
1 3 6
5 10
1 2 110
1 3 120
1 4 130
1 5 120
2 3 110
2 4 120
2 5 130
3 4 120
3 5 110
4 5 120
5 10
1 2 9384
1 3 887
1 4 2778
1 5 6916
2 3 7794
2 4 8336
2 5 5387
3 4 493
3 5 6650
4 5 1422
5 8
1 2 1
2 3 100
3 4 100
4 5 100
1 5 50
2 5 50
3 5 50
4 1 150
0 0

Sample Output

1
20
0
-1
-1
1
0
1686
50

 

题意：

一个图可能会构成多个生成树，那么求其中生成树中最小的一条边与最大的一条边之差最小的是多少。

 

 

题解：

这题虽然不是求最小生成树，但是也很类似。 按照Kruskal的方法，把所有边排序，然后依次枚举最小边，开始构造生成树，取差值最小的便是。

 介绍一下kruskal算法：

这个算法是基于并查集的，每次从图中未加入树种的边种找到边权最小的看，这两个点的祖先是否是一个，如果是一个说明两个点已经是一个树上的了，不做操作，如果两个点来自不同的树即有不同的祖先，那么就把这两个点所代表的两个树合并起来，最后当所有的点都在一棵树上的时候停止操作，一般用合并次数来控制，即n个点需要合并n-1次，所以最好合并操作写在kruskal函数内部，这样方便统计步数

下面是这个题的代码，一定要 注意点的编号是从1开始还是从0开始，wa了好多次

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 const int N = ;
 const int INF = ;
 struct Edge{
     int from;
     int to;
     int w;
     bool operator < (const Edge &a) const
     {
         return w<a.w;
     }
 }edge[N*N];
 int fa[N];
 int Getfa(int x){return (fa[x]==x)?x:fa[x] = Getfa(fa[x]); }
 int fl;
 int n,m;
 bool solve(int x){
     int cnt = ;//共合n-1次结束
     for(int i = ; i <= n; i++) fa[i] = i;//注意点是从1开始编号的
     for(int i = x; i < m; i++){
         int X = Getfa(edge[i].from);
         int Y = Getfa(edge[i].to);
         if(X != Y){
             fa[X] = Y;
             cnt++;
             if(cnt==n-){ fl = edge[i].w;return true;}
         }
     }
     return false;
 }

 int main()
 {
     while(~scanf("%d%d",&n,&m))
     {
         if(n==&&m==) return ;
         for(int i = ; i < m; i++)
         {
             scanf("%d%d%d",&edge[i].from,&edge[i].to,&edge[i].w);
         }
         sort(edge,edge+m);
         int ans = INF;
         for(int i = ; i < m; i++){
             if(solve(i)) ans = min(ans,fl-edge[i].w);
         }
         if(ans==INF) puts("-1");
         else printf("%d\n",ans);
     }
     return ;
 }