【割点】【割边】tarjan

洛谷割点模板题——传送门

割边：在连通图中，删除了连通图的某条边后，图不再连通。这样的边被称为割边，也叫做桥。
割点：在连通图中，删除了连通图的某个点以及与这个点相连的边后，图不再连通。这样的点被称为割点。
DFS搜索树：用DFS对图进行遍历时，按照遍历次序的不同，我们可以得到一棵DFS搜索树。

树边：在搜索树中的蓝色线所示，可理解为在DFS过程中访问未访问节点时所经过的边，也称为父子边
回边：在搜索树中的橙色线所示，可理解为在DFS过程中遇到已访问节点时所经过的边，也称为返祖边、后向边
观察DFS搜索树，我们可以发现有两类节点可以成为割点。对根节点u，若其有两棵或两棵以上的子树，则该根结点u为割点；对非叶子节点u(非根节点)，若其中的某棵子树的节点均没有指向u的祖先节点的回边，说明删除u之后，根结点与该棵子树的节点不再连通；则节点u为割点。对于根结点，显然很好处理；但是对于非叶子节点，怎么去判断有没有回边是一个值得深思的问题。我们用dfn[u]记录节点u在DFS过程中被遍历到的次序号，low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小)，那么low[u]的计算过程如下。

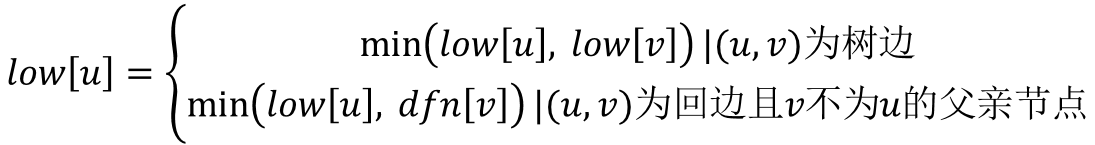
对于给的例子，其求出的dfn和low数组如下。
id     1 2 3 4 5 6
dfn   1 2 3 4 5 6
low   1 1 1 4 4 4
可以发现，对于情况2，当(u,v)为树边且low[v]≥dfn[u]时，节点u才为割点。而当(u,v)为树边且low[v]>dfn[u]时，表示v节点只能通过该边(u,v)与u连通，那么(u,v)即为割边。tarjan算法的时间复杂度是O(n+m)的，非常快。

——附带码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

const int maxn = ;
int n, m, cnt, rp;
int next[ * maxn], to[ * maxn], head[maxn], low[maxn], dfn[maxn], father[maxn];//father为父节点
vector <int> cut_point;
vector < pair <int, int> > cut_edge;

void add(int x, int y)
{
    to[cnt] = y;
    next[cnt] = head[x];
    head[x] = cnt++;
}

void tarjan(int u)
{
    int i, v, child = ;//child表示当前节点孩子数量
    bool flag = ;
    dfn[u] = low[u] = ++rp;
    for(i = head[u]; i != -; i = next[i])
    {
        v = to[i];
        if(!dfn[v])
        {
            child++;
            father[v] = u;
            tarjan(v);
            if(low[v] >= dfn[u]) flag = ;//割点
            if(low[v] > dfn[u]) cut_edge.push_back(make_pair(min(u, v), max(u, v)));//割边
            low[u] = min(low[u], low[v]);
        }
        else if(v != father[u]) low[u] = min(low[u], dfn[v]);

    }
    //根节点若有两棵或两棵以上的子树则该为割点
    //非根节点若所有子树节点均没有指向u的祖先节点的回边则为割点
    if((father[u] ==  && child > ) || (father[u] && flag)) cut_point.push_back(u);
}

int main()
{
    int i, j, x, y, s;
    memset(head, -, sizeof(head));
    scanf("%d %d", &n, &m);
    for(i = ; i <= m; i++)
    {
        scanf("%d %d", &x, &y);
        add(x, y);
        add(y, x);
    }
    for(i = ; i <= n; i++)//图可能不联通（mdzz的洛谷模板题）
     if(!dfn[i])
      tarjan(i);
    sort(cut_point.begin(), cut_point.end());
    s = cut_point.size();
    printf("%d\n", s);
    for(i = ; i < s; i++) printf("%d ", cut_point[i]);//输出割点
    s = cut_edge.size();
    printf("\n%d\n", s);
    for(i = ; i < s; i++) printf("%d %d\n", cut_edge[i].first, cut_edge[i].second);//输出割边
    return ;
}

经过培训，发现上面的代码如果有重边就会拉闸。

下面是可以应对重边的代码

 # include <iostream>
 # include <cstdio>
 # include <cstring>
 # include <string>
 # include <cmath>
 # include <vector>
 # include <map>
 # include <queue>
 # include <cstdlib>
 # define MAXN
 using namespace std;

 inline void File() {
 #ifdef DEBUG
     freopen("in.txt", "r", stdin);
 #else
     //freopen();
     //freopen();
 #endif
 }

 inline int get_num() {
     int k = , f = ;
     char c = getchar();
     for(; !isdigit(c); c = getchar()) if(c == '-') f = -;
     for(; isdigit(c); c = getchar()) k = k *  + c - '';
     return k * f;
 }

 int n, m, tim, cnt;
 int dfn[MAXN], low[MAXN], f[MAXN], to[MAXN], next[MAXN], head[MAXN];
 vector <int> cut_point;
 vector < pair <int, int> > cut_edge;

 inline void add(int x, int y)
 {
     to[cnt] = y;
     next[cnt] = head[x];
     head[x] = cnt++;
 }

 inline void dfs(int u, int fa)
 {
     int i, v, child = ;
     bool flag = ;
     dfn[u] = low[u] = ++tim;
     for(i = head[u]; i != -; i = next[i])
     {
         if((i ^ ) == fa) continue;
         v = to[i];
         if(!dfn[v])
         {
             child++;
             f[v] = u;
             dfs(v, i);
             if(low[v] >= dfn[u]) flag = ;
             if(low[v] > dfn[u]) cut_edge.push_back(make_pair(min(u, v), max(u, v)));
             low[u] = min(low[v], low[u]);
         }
         else low[u] = min(low[u], dfn[v]);
     }
     if((!f[u] && child > ) || (f[u] && flag)) cut_point.push_back(u);
 }

 int main()
 {
     int i, j, x, y;
     n = get_num();
     m = get_num();
     memset(head, -, sizeof(head));
     for(i = ; i <= m; i++)
     {
         x = get_num();
         y = get_num();
         add(x, y);
         add(y, x);
     }
     for(i = ; i <= n; i++)
         if(!dfn[i])
             dfs(i, -);
     for(i = ; i < cut_point.size(); i++) printf("%d\n", cut_point[i]);
     puts("");
     for(i = ; i < cut_edge.size(); i++) printf("%d %d\n", cut_edge[i].first, cut_edge[i].second);
     puts("");
     return ;
 }