U558032 芒果的收获季-区间dp

T4 解析

对于 \(20 \%\) 的数据范围， 保证 \(1\le T \le 20, 1 \le n \le 300,1 \le a_i \le b_i \le 10^4, 1 \le d_i \le 10^4\) ，所有的 \([a_i, b_i]\) 互不包含，

说明每个区域只能单独去采摘，所以答案是 \(\sum d_i\) 。

对于额外的 \(20\%\) 的数据范围，保证 \(1\le T \le 20, 1 \le n \le 300,1 \le a_i \le b_i \le 10^4, 1 \le d_i \le 10^4\) ，所有的 \([a_i, b_i]\) 相等，

说明所有区域成熟的时间相同，可以在同一时间采摘，为了节省距离，直接选择最远的距离即可，答案是 \(max(d_i)\)。

对于 \(100 \%\) 的数据范围，首先考虑将时间看作区间范围，作为 \(x\) 轴的变换方向，另外距离当作 \(y\) 轴，此时将问题转换为区间内选多条直线覆盖所有的区间，如

一条直线覆盖多个区间，取区间的最高的距离当作答案的一部分，求解距离和的最小值。

此时很多同学会想到，直接采用区间贪心的方式，按照右端点从小到大排序，然后进行从右往左进行选择，

如果按照区间贪心的方式，可以获取一部分分数

存在hack数据

1
5
3 4 2
2 8 2
3 4 1
4 5 4
1 3 1

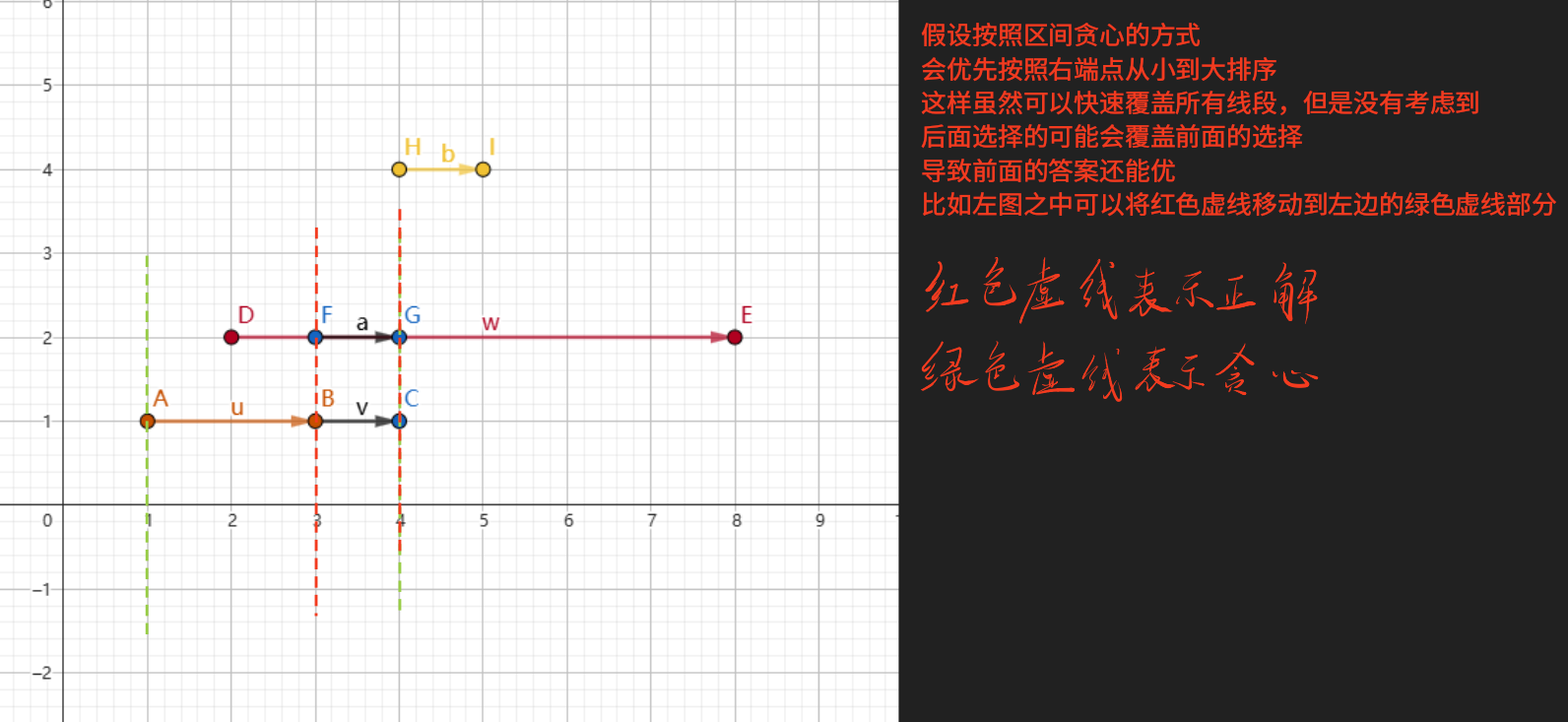
将时间看成横向的 \(x\) 坐标， 距离看成竖向的 \(y\) 坐标之后

发现线段整体是一个区间，考虑区间 \(dp\) 如何计算？这是本题的难点，在此之前可以先把简单的过程写清楚

步骤一、定义状态

\(dp[l][r]\) 表示区间范围 \([l, r]\) 之内覆盖所有线段的距离最小值

步骤二、确定答案

此时因为时间范围有些大，通过离散化的形式，将时间区间转换为 \(600\) 个离散化单位，最终离散化的区间从 \([1, 10000]\) 转换为 \([1, tot]\) 。

答案变成 \(dp[1][tot]\) 。

重点

步骤三、状态转移

先写出状态转移

dp[l][r] = dp[l][m - 1] + dp[m + 1][r] + d, 其中d是区间[l, r] 内完全被包含的线段的最高点

看下图，这里画的竖线表示这里派出了员工，采摘距离最远的 \(4\) ，黄色线段，顺便将下面的暗红色线段 \([2, 8]\) 也给覆盖了，

我们会清晰的发现，在一段区间内，最高点所在的线段的选取，一定会影响它顺便可以覆盖到的答案。

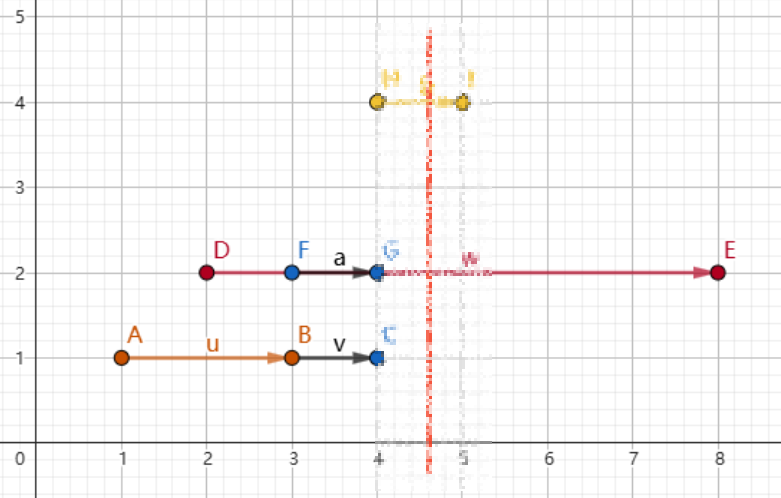
此时我们的答案之和左边区间的答案和右边区间的答案有关，

另外右边区间内出现了 \([2, 8]\) 这条已经被选中的线段，被右边区域包含一部分，

这里不能重复计算，所以我们制定一个规则，参与 \(dp[l][r]\) 答案计算的区间，一定是能够完全被 \([l,r]\) 范围包含的。

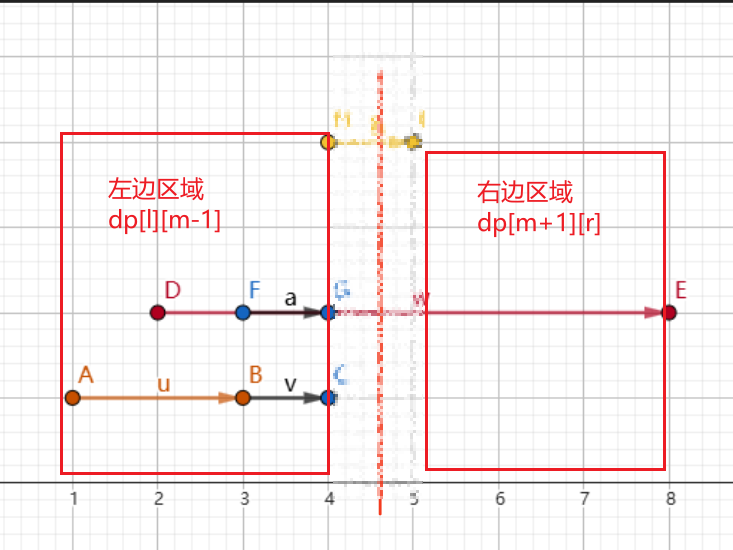
为了方便大家理解，以刚刚左边区间的为例

此时我们的转移断点 \(m\) 只在完全被包含的所有区间内找到的最高的那条范围内

比如此时的 \(m\) 的移动范围是 \([F, G]\) ，为什么 \(D\) 所在的线段不计入答案，因为它只有一部分在区间内，肯定有外面的区间把它包含进去了，比如上面的图。

接下来只需要考虑线段 \([F, G]\) 这个最高的区间范围的影响，在这段范围内，只要选中 \([F, G]\) 之中的任意一点， 此时被覆盖的范围是没有机会的，所以依靠这个

移，然后考虑 dp[l][m - 1] 和 dp[m + 1][r]

因为一定是距离比较低的小区间，比如 \([A, B]\) 先更新，然后区间扩大到 \([A, G]\) 的时候，考虑最高点的影响，

最高点选中之后覆盖的某些高点之后，左侧的最高 dp[l][m - 1] 和右侧的最高 dp[m + 1][r] 的答案，区间是一段一段合并的，所以合并之后，

得到的就是总距离。

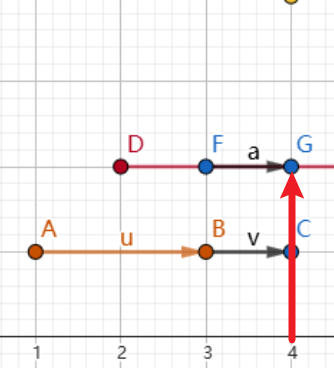
本题属于线段类型的区间 \(dp\) ， 整体思维和实现难度非常高，请同学们反复去看几遍。