AtCoder Beginner Contest 341-F

F - Breakdown

Problem

给你一个由 $N$ 个顶点和 $M$ 条边组成的简单无向图。每个顶点拥有权重$W_i$，并且被放置了$A_i$个棋子。

只要图形上还有棋子，就重复下面的操作：

首先，从图形中选择一个（有棋子的）顶点$x$并移除一个棋子。
从$x$相邻点中选择出一些点组成集合$S$（可以不选），要保证这个集合内的所有点的权重之和小于顶点$x$，即$\sum_{y \in S} W_y \lt W_x$，并在$S$中的每个顶点上放置一个棋子。

请求出最多最多能进行多少次这样的操作。

可以证明，无论如何操作，在有限次迭代后，图形上将没有棋子。

Constraints

$2 \leq N \leq 5000$
$1 \leq M \leq \min \lbrace N(N-1)/2, 5000 \rbrace$
$1 \leq u_i, v_i \leq N$
$u_i \neq v_i$
$i \neq j \implies \lbrace u_i, v_i \rbrace \neq \lbrace u_j, v_j \rbrace$
$1 \leq W_i \leq 5000$
$0 \leq A_i \leq 10^9$

Solution

首先再此解释一下题目中的操作：

假设现在图是这样的：

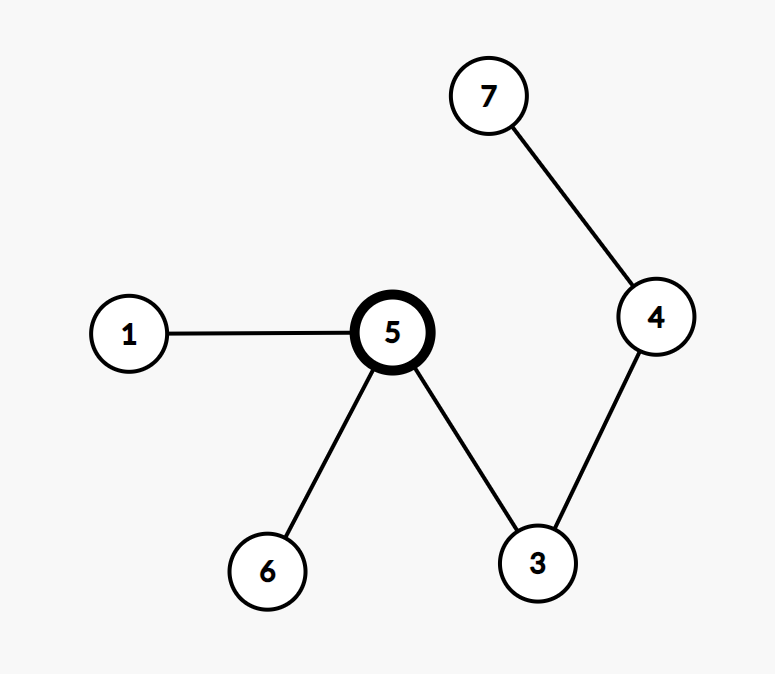
（为了方便，图中的数字既表示顶点，同时也表示该点的权重$W_i$）

其中顶点5上有一颗棋子，并且现在选择$x=5$，开始操作。

首先取下5上的棋子，接下来选择5的相邻点的一个集合（比如1,3），且保证集合内点的权重之和小于$W_x$。因此我们可以选1,3，可以选1，可以选3，也可以不选，但是不能选6。

此时可以发现，我们始终只能选择比点$x$要小的点，也就是说棋子的扩散方向永远是单向的（3永远不可能给5棋子，5也永远不能给6棋子）

所以题目中说的简单无向图其实是个幌子，这其实是一个DAG

那么我们先将原图化为DAG，再按照权重升序来看各个顶点（小权重顶点不会对大权重顶点有干扰，棋子之间也不会有相互作用），进行DAG上的dp。

具体的，设X[i]表示若顶点i有一枚棋子，可以操作的次数

当轮到点x的时候，权重比其小的出点都已经计算好了X[i]，现在需要抉择出如何选择他的出点集合，使得在权重之和不超过$W_x$的情况下，尽力包含更多的X[i]——相当于做个背包问题了。

Code

#define N 5020

int n,m;

vector<pair<int,int>>edge;

int W[N],A[N];

pair<int,int>ww[N];

vector<int>e[N];

int order[N];

bool cmp(int x,int y)

{

	return W[x]<W[y];

}

LL dp[N];

LL X[N];

int main()

{

	cin>>n>>m;

	for(int i=0;i<m;i++)

	{

		int x,y;

		cin>>x>>y;

		edge.push_back(make_pair(x,y));

	}

	for(int i=1;i<=n;i++)

	{

		cin>>W[i];

	}

	for(int i=1;i<=n;i++)

	{

		cin>>A[i];

	}

	for(int i=0;i<m;i++)

	{

		if(W[edge[i].first]>W[edge[i].second]) e[edge[i].first].push_back(edge[i].second);

		if(W[edge[i].first]<W[edge[i].second]) e[edge[i].second].push_back(edge[i].first);

	}

	for(int i=1;i<=n;i++) order[i]=i;

	sort(order+1,order+n+1,cmp);

	for(int i=1;i<=n;i++) X[i]=1;

	for(int i=1,x;i<=n;i++)

	{

		x=order[i];

		memset(dp,0,sizeof(dp));

		dp[0]=1;

		for(unsigned int j=0;j<e[x].size();j++)

		{

			int y=e[x][j];

			for(int k=W[x]-1;k-W[y]>=0;k--)

			{

				dp[k]=max(dp[k],dp[k-W[y]]+X[y]);

			}

		}

		for(int k=0;k<=5000;k++) X[x]=max(X[x],dp[k]);

	}

	LL ans=0;

	for(int i=1;i<=n;i++) ans+=X[i]*A[i];

	cout<<ans;

	return 0;

}

Attention

记得开long long

注意背包dp[i]与X[i]的初值

Reference

A-F in 4 minutes