改进的SMO算法

S. S. Keerthi等人在Improvements to Platt’s SMO Algorithm for SVM Classifier Design一文中提出了对SMO算法的改进，纵观SMO算法，其核心是怎么选择每轮优化的两个拉格朗日乘子，标准的SMO算法是通过判断乘子是否违反原问题的KKT条件来选择待优化乘子的，由KKT条件：

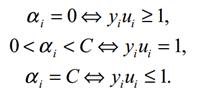
是否违反它，与这几个因素相关：拉格朗日乘子 、样本标记 、偏置b 。 b的更新依赖于两个优化拉格朗日乘子，这就可能出现这种情况：拉格朗日乘子 已经能使目标函数达到最优，而SMO算法本身并不能确定当前由于两个优化拉格朗日乘子计算得到的b是否就是使目标函数达到最优的那个b，换句话说，对一些本来不违反KKT条件的点，由于上次迭代选择了不合适的，使得它们出现违反KKT条件的情况，导致后续出现一些耗时而无用的搜索，针对标准SMO的缺点，出现了以下改进方法。

对于SVM的最优化问题的解：

定义：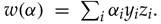

是拉格朗日乘子，通过解下面对偶问题，我们可以得到：

一旦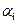确定，其他参数如：就很容易由KKT条件确定了，并且解是不唯一的，最后得拉格朗日函数如下：

定义：

则对偶问题的KKT条件如下：

这个条件可以简化成下面三种情况：

1.：

2.

3．

定义如下数集：I0 = {i: 0 < αi < C}; I1 ={i: yi = 1,αi = 0}; I2 = {i: yi = −1,αi = C}; I3 = {i: yi = 1,αi = C};I4 = {i: yi = −1,αi = 0}.

可以看到以上的KKT条件成立当且仅当有一个使得下式成立：

定义：

当且仅当blow ≤ bup.成立时KKT条件成立。更进一步KKT条件可以写成如下形式：

是一个正的容忍因子。