Another kind of Fibonacci(hdu3306)

Another kind of Fibonacci

Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 2353    Accepted Submission(s): 936

Problem Description

As
we all known , the Fibonacci series : F(0) = 1, F(1) = 1, F(N) = F(N -
1) + F(N - 2) (N >= 2).Now we define another kind of Fibonacci : A(0)
= 1 , A(1) = 1 , A(N) = X * A(N - 1) + Y * A(N - 2) (N >= 2).And we
want to Calculate S(N) , S(N) = A(0)² +A(1)²+……+A(n)².

 

Input

There are several test cases.
Each test case will contain three integers , N, X , Y .
N : 2<= N <= 2³¹ – 1
X : 2<= X <= 2³¹– 1
Y : 2<= Y <= 2³¹ – 1

 

Output

For each test case , output the answer of S(n).If the answer is too big , divide it by 10007 and give me the reminder.

 

Sample Input

2 1 1

3 2 3

 

Sample Output

6

196

 思路：矩阵快速幂；

S(n) = ∑f(n)2 = S(n-1)+f(n)2 = S(n-1)+x2f(n-1)2+y2f(n-2)2+2xyf(n-1)f(n-2)；

然后f(n)*f(n-1) = (x*f(n-1)+y*f(n-2))*f(n-1) = x*f(n-1)2+y*f(n-1)*f(n-2)；

然后构造矩阵；

其中的第三个矩阵写错了，应该是s[n-1];     f[n-1]^2;     f[n-2]^2;  f[n-1]*f[n-2];

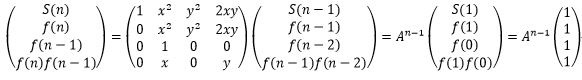
 1 #include<stdio.h>
 2 #include<algorithm>
 3 #include<iostream>
 4 #include<string.h>
 5 #include<queue>
 6 #include<set>
 7 #include<math.h>
 8 #include<map>
 9 using namespace std;
10 typedef struct node
11 {
12         int m[4][4];
13         node()
14         {
15                 memset(m,0,sizeof(m));
16         }
17 } maxtr;
18 void Init(maxtr *ans,int x,int y);
19 maxtr E();
20 maxtr quick_m(maxtr ak,int m);
21 const int mod = 10007;
22 int main(void)
23 {
24         int n,x,y;
25         while(scanf("%d %d %d",&n,&x,&y)!=EOF)
26         {
27                 int f1 = 2;
28                 int a1 = 1;
29                 int a0 = 1;
30                 int xx = 1;
31                 maxtr ask ;
32                 Init(&ask,x,y);
33                 maxtr tp = quick_m(ask,n-1);
34                 printf("%d\n",(tp.m[0][0]*2+tp.m[0][1]*a1+tp.m[0][2]*a0+tp.m[0][3]*xx)%mod);
35         }
36         return 0;
37 }
38 void Init(maxtr *ans,int x,int y)
39 {      memset(ans->m,0,sizeof(ans->m));
40         x%=mod;y%=mod;
41         ans->m[0][0] = 1;
42         ans->m[0][1] = x*x%mod;
43         ans->m[0][2] = y*y%mod;
44         ans->m[0][3] =2*x*y%mod;
45         ans->m[1][1] = x*x%mod;
46         ans->m[1][2] = y*y%mod;
47         ans->m[1][3] = 2*x*y%mod;
48         ans->m[2][1] = 1;
49         ans->m[3][1] = x%mod;
50         ans->m[3][3] = y%mod;
51 }
52 maxtr E()
53 {
54         maxtr ak;
55         int i,j;
56         for(i = 0; i < 4; i++)
57         {
58                 for(j = 0; j < 4; j++)
59                 {
60                         if(i == j)
61                                 ak.m[i][j]  = 1;
62                 }
63         }
64         return ak;
65 }
66 maxtr quick_m(maxtr ak,int m)
67 {
68         int i,j;
69         maxtr ac = E();
70         while(m)
71         {
72                 if(m&1)
73                 {
74                         maxtr a;
75                         for(i = 0; i < 4; i++)
76                                 for(j = 0; j < 4; j++)
77                                         for(int s= 0; s < 4; s++)
78                                                 a.m[i][j] = (a.m[i][j] + ak.m[i][s]*ac.m[s][j]%mod)%mod;
79                         ac = a;
80                 }
81                 maxtr b;
82                 for(i = 0; i < 4; i++)
83                         for(j = 0; j < 4; j++)
84                                 for(int s = 0; s < 4; s++)
85                                         b.m[i][j] = (b.m[i][j] + ak.m[i][s]*ak.m[s][j]%mod)%mod;
86                 ak = b;
87                 m>>=1;
88         }
89         return ac;
90 }