OO第三次博客作业--第三单元总结

一、JML 语言的理论基础及应用工具链

JML 是一种行为接口规格语言，提供了对方法和类型的规格定义手段。通过 JML 和其支持工具，不仅可以基于规格自动构造测试用例，并整合了 SMT Solver 等工具以静态方式来检查代码实现对规格的满足情况。

1.1 方法规格

JML 中的前置条件指的是在调用方法之前必须要满足的条件；
后置条件指的是该方法返回时必须要满足的条件，即制定了该方法的指责；
副作用范围限定指的是在执行过程中可能（允许）被修改的对象的属性数据或者类的静态成员变量。

1.2 类型规格

JML 中不变式 (invariant) 是要求在所以可见状态下都必须满足的特性，语法上定义 invariant P，其中 invariant 为关键词，P 为谓词；
状态变化约束 (constraint) 是指对象的状态在变化时也需要满足的一些约束，这些约束在本质上也是一种不变式。

1.3 应用工具链

openJML
JMLUnitNG

二、 JMLUnitNG

我使用 JMLUnitNG 组件的流程如下：

下载并安装 JMLUnitNG 组件
使用 JMLUnitNG 生成测试类
在 IDEA 中运行测试类

我首先对一个简单的方法 Demo.java 进行了测试：

通过命令行输入 java -jar jmlunitng.jar Demo.java 生成测试类，然后在测试类目录下建立 project，直接在 IDEA 中运行 Demo_JML_Test 即可。

我生成的测试数据如下：

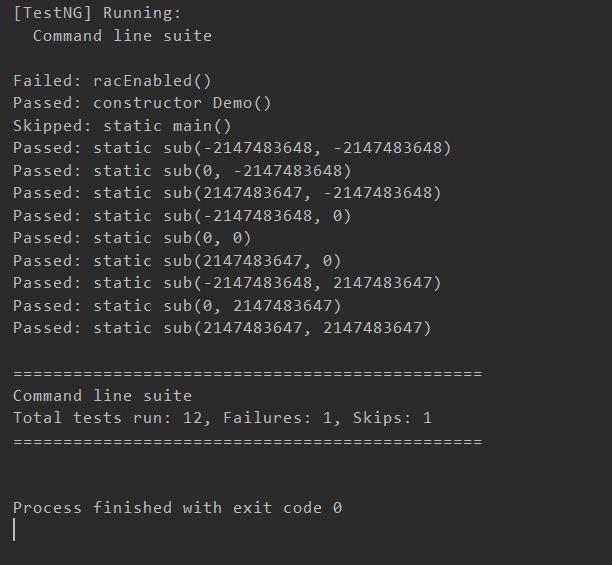
三、梳理架构设计，分析迭代中对架构的重构

第一次作业

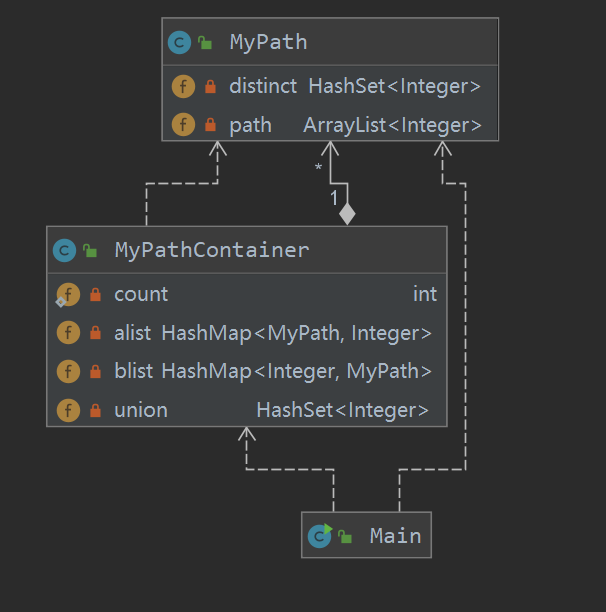
完全按照官方接口建立。

其中 union 记录的是整个 container 中的不同的节点，每次 container 中的路径变化，更新一次 union。

第二次作业

第二次作业将第一次中的 MyPathContainer 部分方法复制到 MyGraph 中，然后根据接口添加了新的方法，其他大致都没变。

第三次作业

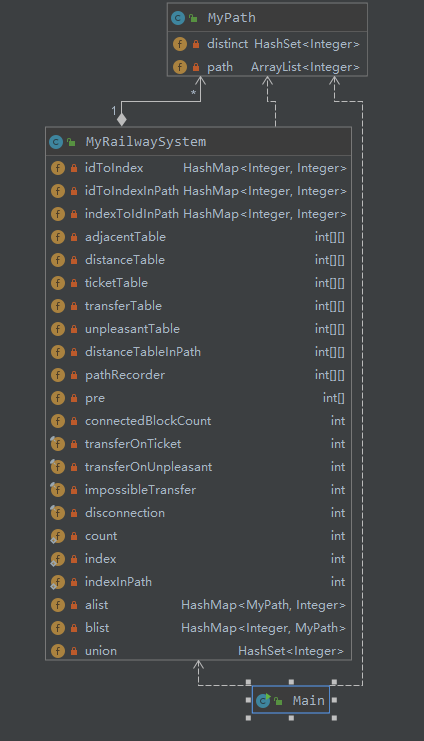
第三次作业将第二次作业中的 MyGraph 中部分方法复制过去，然后根据接口添加了新的方法。

这一次作业比上一次添加了很多要求，且复杂度更高了，并且涉及到一些算法上的问题。

我使用的是讨论区大佬的不拆点的算法，用四个数组分别记录、完成四种功能，但其实都是基于最短路径的，只是每种功能中路径的权不同而已。每次更新 Path 时需要更新四个数组，且做四次floyd 。但因为常数较小，所以时间相对较短。

四、分析代码实现的bug和修复情况

第一次作业中，在 MyPath 中实现的 compare 方法中出现了一个小 bug，是我在遇到不相同的节点时，返回的是两值相减的值，这时没有考虑到可能会溢出。修复改为返回两值比较的布尔值。

第二次作业中吸取了第一次作业的教训，认真阅读规格，没有出现Bug。

第三次作业由于比前两次多了很多复杂的逻辑，而我的架构并不适于拓展，慌忙之下写出了一个较为严重的bug。在 containsEdge() 方法中，由于没有认真看规格，将两个同节点算作存在这条边，但实际不应该算作边；另外，在计算 least unpleasant value 时，我的方法需要在每个 path 内部另外计算 path 内节点的 least unpleasant value ，本来可以直接套用计算整个地铁系统的方法，我却另外想了一个更复杂的方法，既添了麻烦又出了错。已经修复为更简单的方法，即将路径权设为 unpleasant value ，然后跑 floyd。

五、对规格撰写和理解上的心得体会

对于一些较为复杂的方法，其规格的逻辑表达式很长，需要认真仔细地阅读，搞清楚前置条件和后置条件。
规格只给出了需要实现的功能，而没有要求如何实现，所以仍需要考虑架构和算法上的设计。