为什么CTR预估使用AUC来评估模型？

　　ctr预估简单的解释就是预测用户的点击item的概率。为什么一个回归的问题需要使用分类的方法来评估，这真是一个好问题，尝试从下面几个关键问题去回答。

　　1、ctr预估是特殊的回归问题

　　ctr预估的目标函数为

　　　　　　　　　　　　　　　　　　　　　　　　f(x)=P(+1|x)

　　特殊之处在于目标函数的值域为[0,1]，而且由于是条件概率，具有如下特性

　　　　　　　　　　

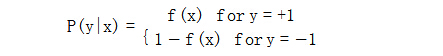
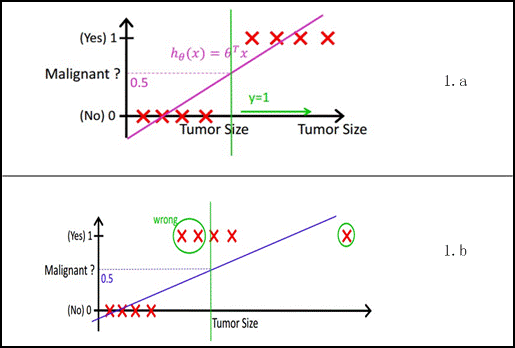
　　如果将ctr预估按照一般的回归问题处理（如使用Linear Regression），面临的问题是一般的linear regression的值域范围是实数域，对于整个实数域的敏感程度是相同的，所以直接使用一般的linear regression来建立ctr预估模型很容易受到noise的影响。以Andrew Ng课程中的例子图1.b所示，增加一个噪音点后，拟合的直线马上偏移。另外，由于目标函数是条件概率，训练样本中会存在特征x完全相同，y为+1和-1的样本都出现的问题，在linear regression看来是一个矛盾的问题，而Logistics Regression很好的解决了这个问题[1]。

　　　　　　　　　　

　　2、LR模型的cost function不使用平方差

　　一般回归问题采用的cost function是预测值和实际值的平方差，而LR模型无法采用平方差作为cost function的原因是由于基于LR模型公式的平方差函数是非凸函数，无法方便的获得全局最优解。

　　LR模型采用的cost function是采用cross-entropy error function（也有叫做对数似然函数的），error measure是模型假设h产生训练样本D的可能性（likelihood）[2]。

　　假设y1=+1, y2=-1, ......., yn=-1，对应的likelihood为：

　　

　　

　　3、为什么AUC也可以用于LR模型的评估

　　普遍上对于AUC的认识是在分类问题中，取不同的threshold后，在横坐标false positive rate，纵坐标为true positive rate平面上绘制ROC曲线的曲线下面积，所以很难理解是如何与这里的回归问题联系起来。实际上，一个关于AUC的很有趣的性质是：它和Wilcoxon-Mann-Witney Test是等价的[3]。而Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本，正类样本的score有多大的概率大于负类样本的score。有了这个定义，我们就得到了另外一种计算AUC的方法：具体来说就算统计一下所有M*N（M为正类样本的数目，N为负类样本的数目）个正负样本对中，有多少个组中的正样本的score大于负样本的score。

　　

　　

　　

　　参考文献

　　[1]逻辑回归模型(Logistic Regression, LR)基础。 http://www.cnblogs.com/sparkwen/p/3441197.html

　　[2] Machine Learning Foundation, Coursera.

　　[3]AUC(Area Under roc Curve )计算及其与ROC的关系 http://www.cnblogs.com/guolei/archive/2013/05/23/3095747.html

　　原文连接：

　　https://www.evernote.com/shard/s66/sh/8f1d15c8-48b6-4b34-a4bc-89a60c09d724/a3bbdc80ade0c94b014910321eb4a10c#