Maths | 层次分析法（Analytic Hierarchy Process）

目录

• 1. 概述
• 2. AHP算法
  • 2.1. 建立层级
  • 2.2. 构造 成对 比较 矩阵
  • 2.3. 成对比较矩阵的 一致性检验 与 层次单排序
  • 2.4. 层次总排序

参考：

1. （中文）https://zhuanlan.zhihu.com/p/35051786
2. （中文繁体）www.nhu.edu.tw/~ykhuang/AHP.doc
3. （英文，作者即AHP提出者，美国运筹学家、匹兹堡大学T. L. Saaty教授）THE ANALYTIC HIERARCHY PROCESS-WHAT IT IS AND HOW IT IS USED

1. 概述

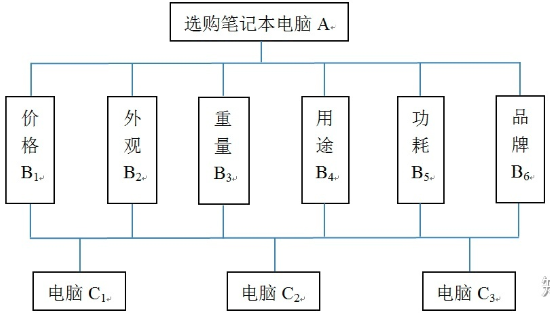
我们遇到的大多数问题（决策目标），都可以逐层拆解为：准则，子准则，……，最底层即所有的可选方案。
拆解层级如图。注意对于父层的每一个因素，必须包含（联系于）子层的所有因素。

我们知道，大多数决策过程既存在客观成分（客观指标），也存在主观因素（心理，偏好等）。
AHP正是一种很好的解决方案，可以结合主、客观因素，定量作出决策。

作者的原话是：

For a long time people have been concerned with the measurement of both physical and psychological events. By physical...
By contrast, the psychological is the realm of the intangibles as it relates to subjective ideas and beliefs of the individual about himself of herself and the world of experience. The question is whether there is a coherent theory that can deal with both these worlds of reality without compromising either. The AHP is a method that can be used to establish measures in both the physical and social domains.

由于AHP的本质方法是计算各个因素的权值，因此也常用于对各影响因素进行重要性排序。
实际上，人作决策时往往也会对各参考因素排序，因此AHP和人的决策过程具有一致性。

2. AHP算法

2.1. 建立层级

对于一个既定决策目标（目标层），我们将其逐层拆解为多层，名为准则层；最底层即方案层。
AHP的最终目标，就是确定方案层中的每一个方案，对于目标层的相对权重。

如上图，“选购笔记本”属于目标层，三款电脑属于方案层，中间的参考因素都属于准则层。

注意，同一层级的元素之间必须是相互独立的(Independence)，否则，应考虑网络分析法ANP。

2.2. 构造 成对 比较 矩阵

假设某\(f_1\)层有一个元素source。我们想探究，下一层\(f_2\)中的所有元素，对于source元素而言的重要性。
绝对重要性是很难量化的，但相对重要性比较好量化。
因此我们构造如下矩阵：

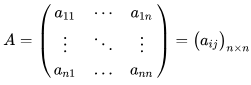
其中，\(a_{ij} = \frac{w_{i}}{w_{j}}\)代表：\(f_2\)层中，\(i\)元素与\(j\)元素相比，对于\(f_1\)层source元素的相对重要程度。\(w_{i}\)即该层级中准则\(i\)的绝对权重。
Saaty建议用整数\(1\)到\(9\)及其倒数，作为\(a_{ij}\)的值域。该值域又称为比例尺度Ratio Scale。
比如，若\(a_{ij}=9\)，那么与\(j\)元素相比，\(i\)元素对于source元素绝对重要得多得多得多得多。
又如，若\(a_{ij}=1\)，那么\(j\)和\(i\)元素对于source元素是同等重要的。

显然，成对比较矩阵元素\(a_{ij}\)满足：

1. \(a_{ij}>0\)
2. \(a_{ji} = \frac{w_{j}}{w_{i}} = \frac{1}{\frac{w_{i}}{w_{j}}} = \frac{1}{a_{ji}}\)
3. \(a_{ii}=1\)

基于以上特点，该矩阵又称为正互反矩阵(Positive Reciprocal Matrix)。

由于相对重要性的判断容易出现偏差，因此Saaty建议同一层级的元素不要超过7个。作者原话是：

The question is, "How much should one include in a hierarchy?" A general rule is that the hierarchy should be complex enough to capture the situation, but small and nimble enough to be sensitive to changes.

2.3. 成对比较矩阵的 一致性检验 与 层次单排序

假设\(i\)元素（对source元素）的重要性是\(j\)元素的3倍，\(j\)元素的重要性是\(k\)元素的2倍。
那么符合直觉的是：\(i\)元素（对source元素）的重要性是\(k\)元素的6倍。
这就称为传递性(Transitivity)，也称为一致性(Consistency)。

若一个成对比较矩阵中的元素都满足：\(a_{ik} \cdot a_{kj} = a_{ij}\)，则称\((a_{ij})_{n \times n}\)为一致性矩阵。判断定理如下：
定理：\(n\)阶正互反矩阵\(A\)为一致性矩阵，等价于：\(A\)的最大特征值\({\lambda}_{max} = n\)，其余特征值为0。
证明：参见这篇论文

其中关键的一点是：设\(\overline{w} = (w_1,w_2,\cdots,w_n)^T\)是权值向量，那么有\(A\overline{w} = n\overline{w}\)，特征向量\(\overline{w}\)对应的特征值就是\(n\)。

实际操作中，我们难遇完全一致的成对比交矩阵，一是因为客观事物并不简单（相互关联等），二是人的判断有主观性。
因此，Saaty建议先求出\(A\)的最大特征值，其对应的特征向量归一化后（使元素和为1）即权值向量。这一过程称为层次单排序。
在实际应用中，最大特征值往往是近似求解的。可以参见各路PPT。

但是显然，这种近似是有条件的：\(A\)需要满足一定程度的一致性。
一致性指标(Consistence Index)的检验方法，就称为一致性检验：\(CI = \frac{\lambda_{max}-n}{n-1}\)。
显然，当\(CI = 0\)时，表示完全一致；\(CI\)越大，一致性越差。
CI是否能为负？正互反矩阵的最大特征值是否一定不小于其阶数？考证了很久没得到结果。。

Oak Ridge National Laboratory & Wharton School进行了一项研究。假设\(A\)具有某一阶数，其值是随机生成的。
经过1000次随机模拟后，我们统计了平均的\(CI\)值：

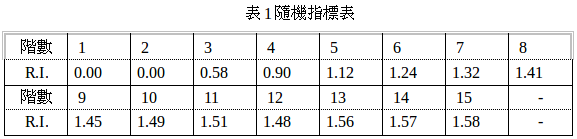
这又称为随机性指标(Random Index)。显然，如果我们的\(A\)具有和\(RI\)相近的\(CI\)，那么我们的矩阵很可能是无效的。

因此规定，只有当一致性比率(Consistency Ratio)\(CR = \frac{CI}{RI} <0.1\)时，一致性才令人满意。

2.4. 层次总排序

在层次单排序后，我们把各层权重合成。合成后也可以计算一致性指标，但通常不予考虑。详见第一个参考链接。