pytest 1.简单介绍一，安装和如何运行

一、pytest是一个接口测试框架，试用版起来比较轻便灵活。首先来介绍他的安装：

直接使用命令 ： pip install -U pytest

通过命令 ：pytest --version  来查看版本信息

二、首先来创建第一个简单的demo，可以在pycharm里面创建，并且运行，运行只需要配置一下就可以

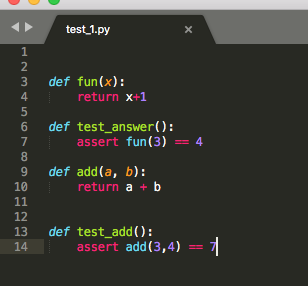
# content of test_1.py
def func(x):
    return x + 1

def test_answer():
    assert func(3) == 5

如何运行呢？ 首先，测试的方法必须是test_开头，文件名字是 test_*.py or *_test.py，如果在pycharm中的话，名字可以随意起。
两种运行方式：
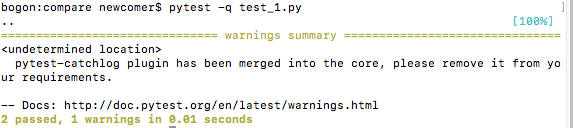
1、进入到文件当前目录，然后输入命令pytest   就会执行所有的文件，也可以指定要执行的文件：pytest -q test_？？.py

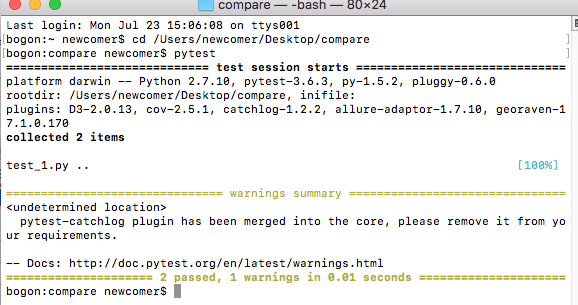
指定执行的文件名字

2、在pycharm里面配置如下：

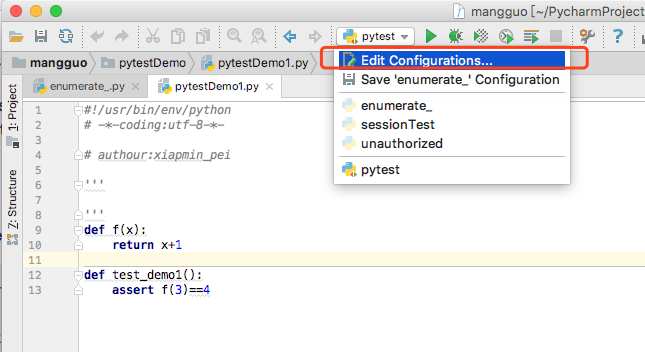
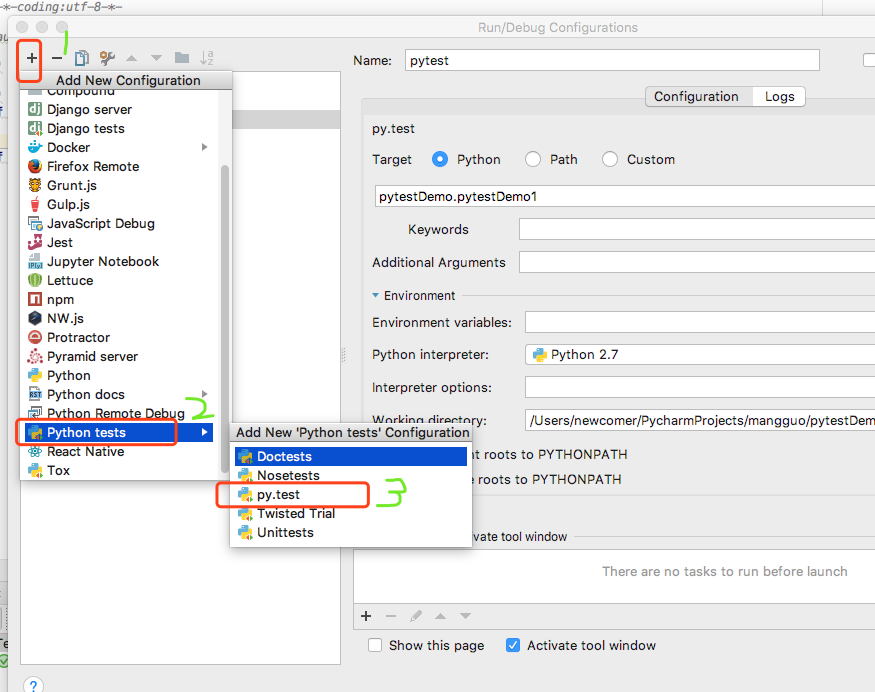
Name随便起一个名字，我起名为pytest

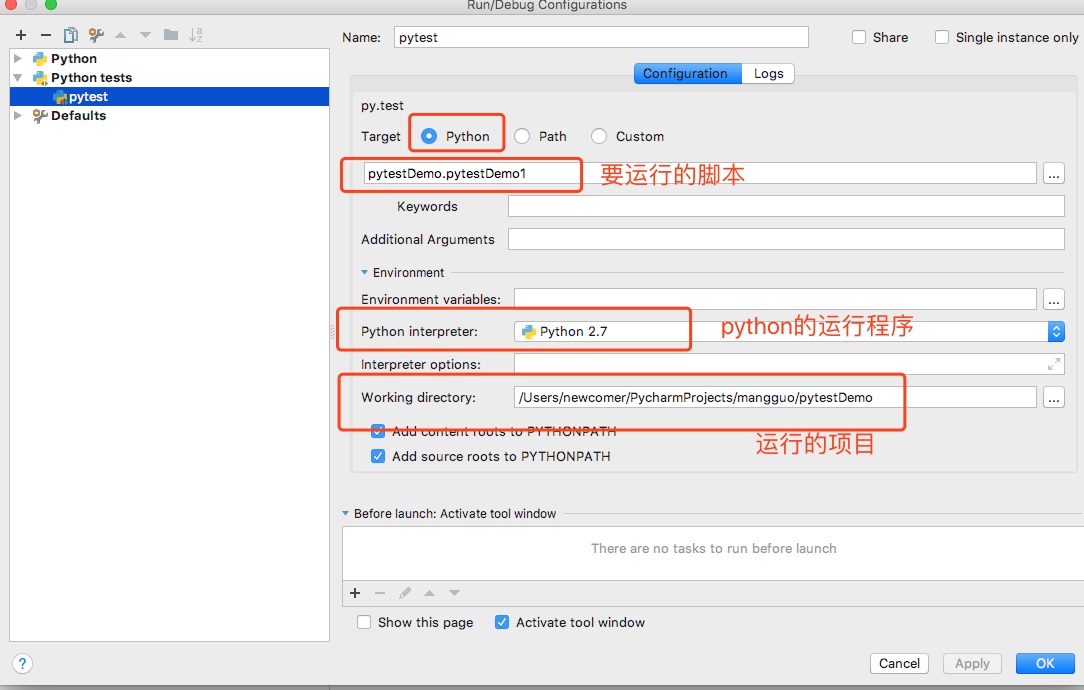
以下是运行结果：

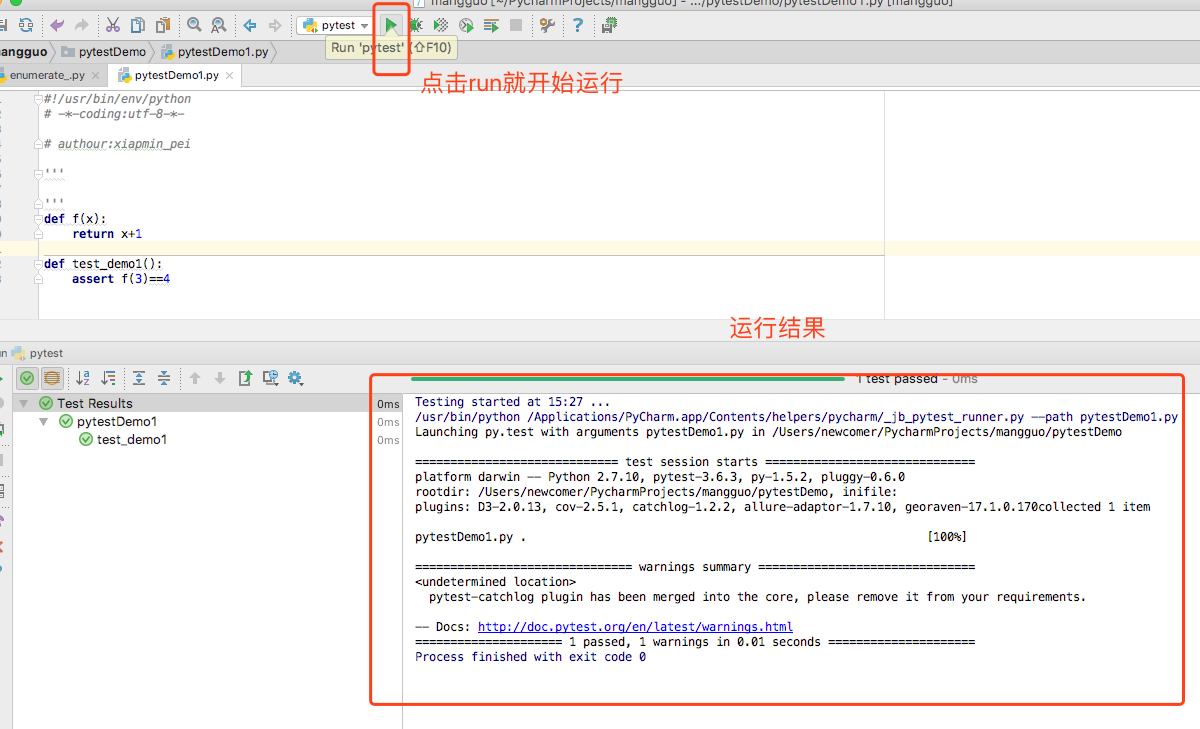
换成类也是一样的，多个测试方法在同一个类中：

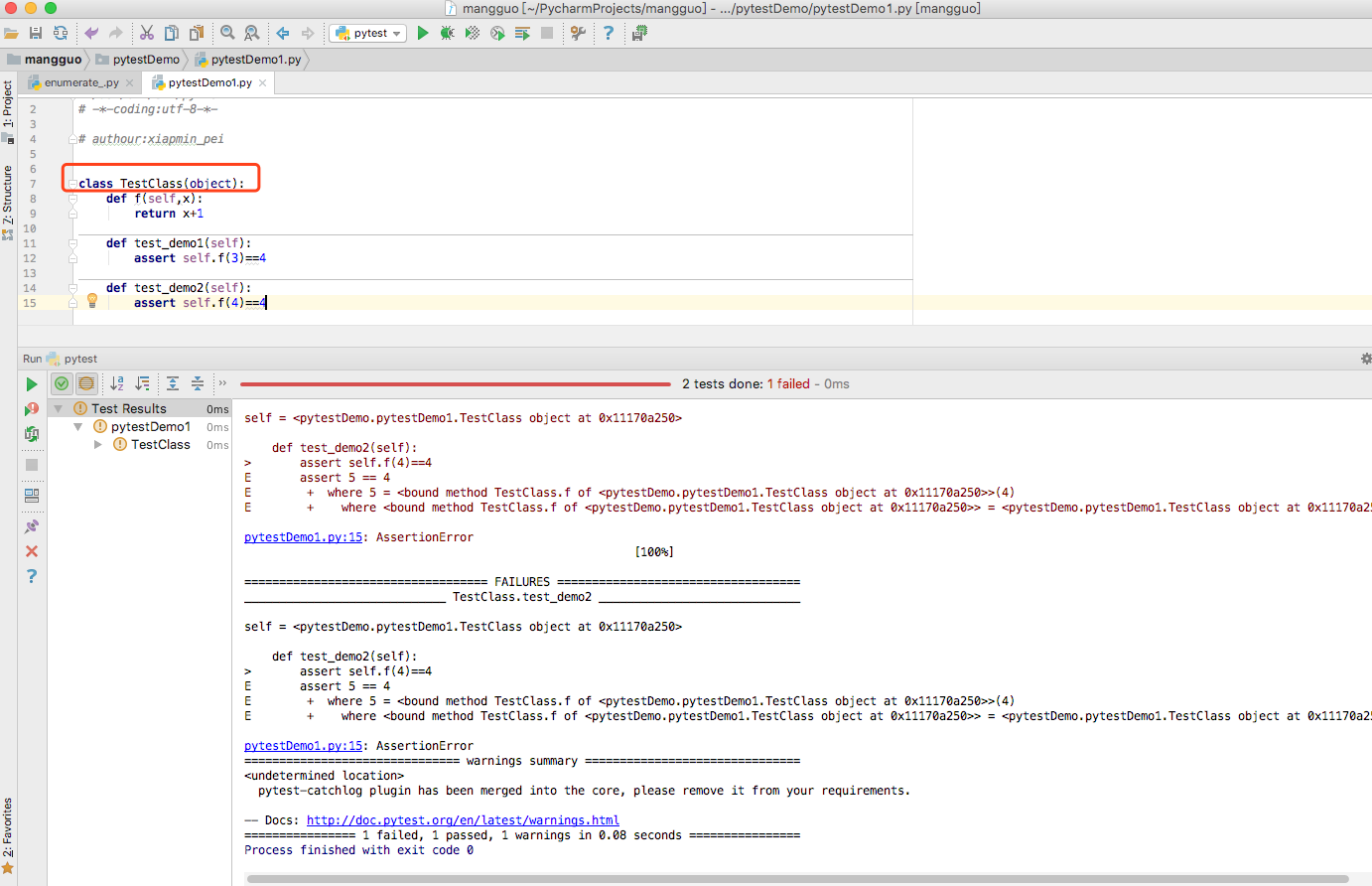
运行的一些命令：

pytest test_mod.py    运行一个具体的模块

pytest testing/       运行一个路径下的所有case

pytest -k "MyClass and not method"    运行包含MYClass类中的case，但是不包含名字为“method”这个case

pytest test_mod.py::test_func   运行模块中的方法

pytest test_mod.py::TestClass::test_method  运行模块中的类中的方法

pytest -m slow   将会运行所有被装饰器装饰过的方法，比如 @pytest.mark.slow 

pytest --pyargs pkg.testing  运行testing包中的case

pytest -x            # stop after first failure  在第一个case失败以后就停止
pytest --maxfail=2    # stop after two failures   在第二个case失败以后就停止

执行完命令的一些code的含义：

Exit code 0:	All tests were collected and passed successfully，所有的用例都被收集完成而且执行成功
Exit code 1:	Tests were collected and run but some of the tests failed   所有的用例都被收集完成，但是失败了一些
Exit code 2:	Test execution was interrupted by the user    执行过程中被执行者终止
Exit code 3:	Internal error happened while executing tests  执行过程中内部发生错误
Exit code 4:	pytest command line usage error    pytest命令有错误
Exit code 5:	No tests were collected   没有用例被收集