3D Math Keynote 2

【3D Math Keynote 2】

1、方向（diretion），指的是前方朝向。方位（orientation），指的是head、pitch、roll。

　　　　

2、欧拉角的缺点：

　　1）给定方位的表达式不惟一。

　　　　例如，pitch 135 = heading180 + pitch 45 + bank 180。

　　　　通过将 heading、bank 限制在 +180~-180度，pitch限制在+90~-90度即可解决不惟一的问题。

　　2）两个角度间插值非常困难。

3、复数的共轭

　　

　　复数的模。

　　　　

4、复数集存在于一个2D平面上，可以认为这个平面有2个轴：实轴、虚轴。

　　　　

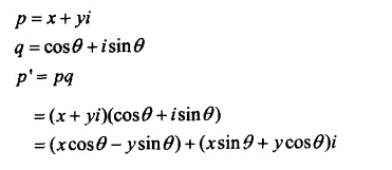
　　四元数有3个虚部，i、j、k。

　　　　

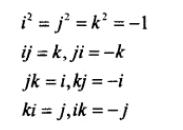
　　绕向量 n 旋转 0 度的四元数：

　　　　

　　q与-q代表的实际角位移是相同的，将0 加上360度，不会改变q的角位移，但q的四个分量都变负了。所以任意角位移有2种四元数的表示法。

　　四元数也有模。

　　　　

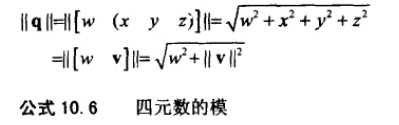
5、四元数的共轭：

　　　　

　　四元数的逆：

　　　　

　　当 |q| 为1时，四元数的共轭，就是四元数的逆。

　　单位四元数：[1, 0]

　　四元数逆意味着向相反的方向旋转相同的角度。

6、四元数乘法。

　　

　　四元数乘法满足结合律，不满足交换律。

　　四元数叉乘的模等于模的积：

　　

　　

　　四元数逆的性质：

　　

7、四元数旋转公式：

　　

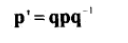
　　下例，先执行a旋转，再执行b旋转：

　　　　

8、四元数点乘。结果是一个标量。

　　

9、四元数的对数。引入变量 alpha = 0/2

　　

　　指数公式为：

　　　　

9.1、四元数求幂。我们看看它的数学定义。
　　

　　结合9中的公式，上式可以推导为 exp(t[0 alpha*n])，也就是 q^t次方，其实是 alpha 乘以了t。所以q^t实际上是 [cos(t*alpha) n.sin(t*alpha)]。

　　下述代码使用上述原理，计算四元数 q 的 t 次方的值。原理是让角度 alpha * t。

　　

　　上面的 if 是用于避免单位四元数[1 0]的情况，单位四元数放大 t 倍，还是单位四元数。

10、slerp 避免了欧拉角插值的所有问题。四元数插值的理论：

　　

　　

　　旋转插值图解：

　　　　

　　

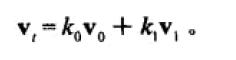
　　由相似三角形原理，可以求出 k0、k1。

　　

　　　　

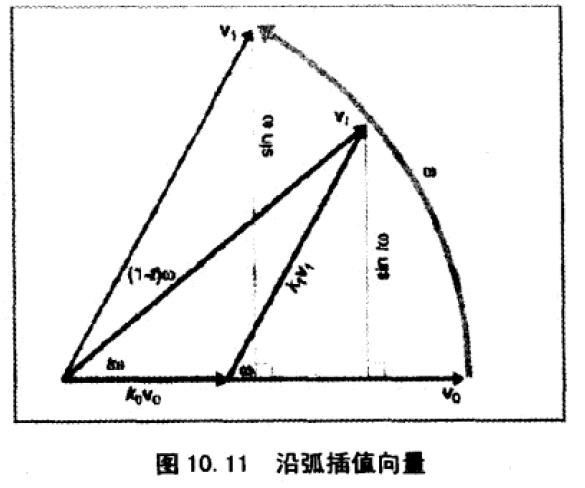
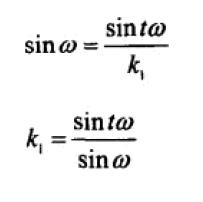
　　所以 V(t) 可以表示为：

　　　　

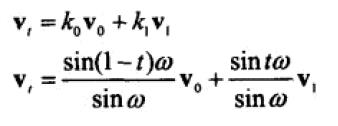
　　扩展到四元数即为：

　　　　

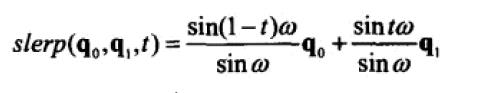
　　slerp 的完整代码如下：

　　　　

　　　　

　　上述实现用了一个书上未证明的公式，四元数的点乘等于夹角的 cos。

　　　　

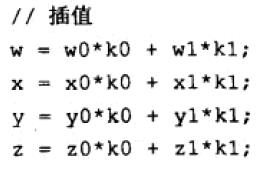
11、squard 是四元数的样条插值。需要引入控制点：

　　

　　可以看到，Si的计算需要引用 qi-1、qi、qi+1。所以在计算转变时，实际需要四个 q点。

　　

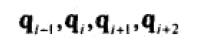
　　样条插值轨迹为：

　　

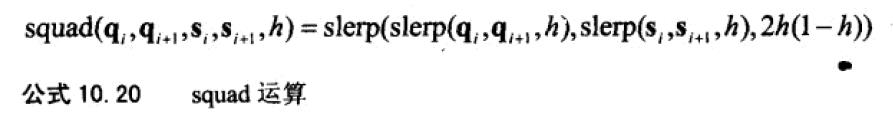
12、从欧拉角到矩阵。

　　从惯性坐标系到物体坐标系非常容易，将3个轴轴的旋转矩阵相乘即可。
　　

　　而从物体坐标系到惯性坐标系，取上面矩阵的转置矩阵即可。

　　

　　

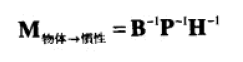
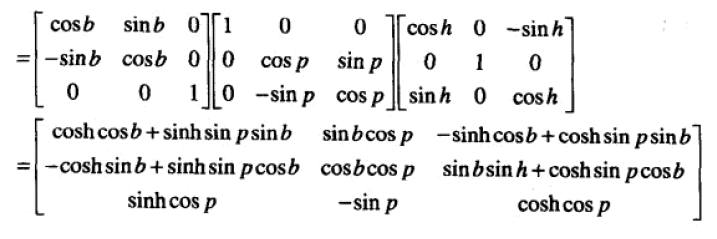
13、从矩阵到欧拉角

　　

　　

　　上面求解出了 pitch，也就推出了 cosp 的值。从而根据 m13、m33 可以推出 sinh、cosh 的的值，然后使用 atan2 即可计算出 h。

　　　　

　　用同样的方式，可以用m21、m22解得 bank。

　　　　

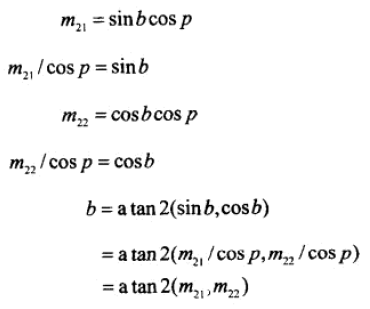
　　若 cosp 为0，则可推出 p 是+/- 90，b 为0。从而可以使用下面的值化简公式：

　　　　 　

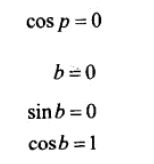
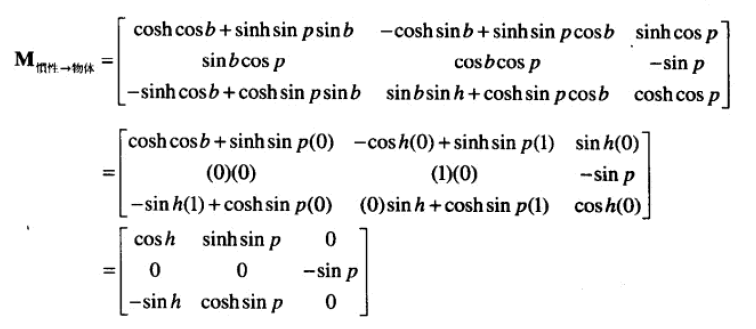
　　通过 m11、m31 可计算出h。

14、实现从矩阵解出欧拉角的算法。

// 设矩阵保存在下面这些变量中
float m11, m12, m13;
float m21,m22,m23;
float m31,m32,m33;

// 以弧度形式计算欧拉角并存在以下变量中
float h,p,b;

// 从m23计算pitch, 小心 asin() 的域错误，因浮点计算我们允许一定的误差
float sp = -m23;
if (sp <= -1.0f){
    p = -1.570796f; // -pi/2
}else if (sp >= 1.0){
    p = 1.570796; // pi/2
} else {
    p = asign(sp);
}

// 检查万象锁的情况，允许一些误差
if (sp > 0.9999f){
    // 向正上或正下看
    // 将 bank 置零，赋值给 heading
    b = 0.0f;
    h = atan2(-m32, m11);
} else {
    // 通过 m12 和 m33 计算heading
    h = atan2(m12, m33);
    b = atan2(m21, m22);
}

15、从四元数转换到矩阵。

　　绕任意轴的旋转矩阵：

　　　　

　　绕任意轴旋转的四元数：

　　

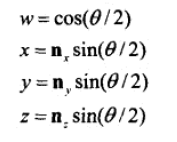
　　我们需要把每一个m推导成为 w,x,y,z 的形式，以m11为例。

　　

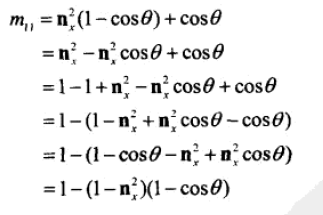
　　使用 cos 倍角公式：

　　　　

　　最后展开化简可得：

　　　　

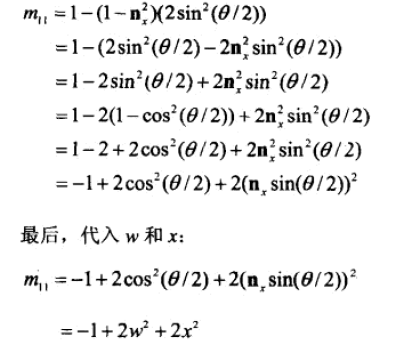
　　其他m求法的就不举例了，是类似的方法。下面是最终答案，从四元数构造出的完整旋转矩阵：

　　　　

　　

16、从矩阵转换到四元数。

　　从直接利用公式 10.23，首先检查对角线元素。

　　　　

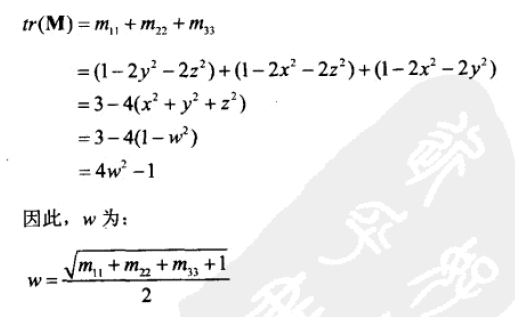
　　可以用有类似的方法求得其他三个元素：

　　　　

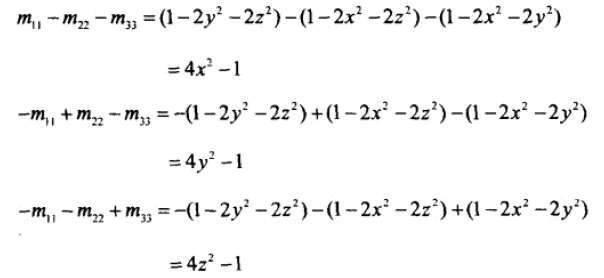
　　因为平方根的结果总是正。另一个技术是检查对称位置上的元素和。

　　　　

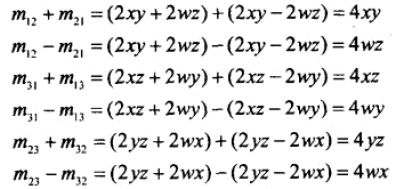
　　首先用第一种方法计算出 w,x,y,z 其中一个的值，然后再用第二种方法，得出另外三个数值的值，即可避免所有元素均为正的问题。
　　　　

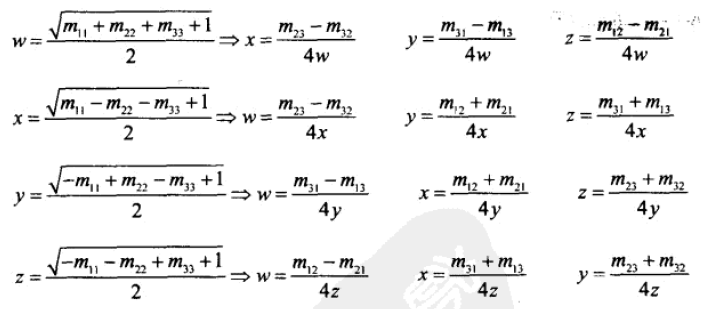
　　下面是算法实现：

// 输入矩阵
float m11, m12, m13;
float m21, m22, m23;
float m31, m32, m33;

// 输出四元数
float w, x, y, z;

// 探测 w, x, y, z 中的最大绝对值
float fourWSquaredMinus1 = m11 + m22 +m33;
float fourXSquaredMinus1 = m11 - m22 - m33;
float fourYSquaredMinus1 = m22-m11-m33;
float fourZSquaredMinus1 = m33 - m11 -m33;

int biggestIndex = ;
float fourBiggestSquaredMinus1 = fourWSquaredMinus1;

if (fourXSquaredMinus1 > fourBiggestSquaredMinus1){
    fourBiggestSquaredMinus1 = fourXSquaredMinus1;
    biggestIndex = ;
}

if (fourYSquaredMinus1 > fourBiggestSquaredMinus1){
    fourBiggestSquaredMinus1 = fourYSquaredMinus1;
    biggestIndex = ;
}

if (fourZSquaredMinus1 > fourBiggestSquaredMinus1){
    fourBiggestSquaredMinus1 = fourZSquaredMinus1;
    biggestIndex = ;
}

// 计算平方根和除法
float biggestVal = sqrt(fourBiggestSquaredMinus1 + 1.0f) * 0.5f;
float mult = 0.25f / biggestVal;

// 计算四元数的值
switch(biggestIndex){
case :
    w = biggestVal;
    x = (m23-m32)*mult;
    y = (m31-m13)*mult;
    z = (m12 - m21) * mult;
    break;
case :
    x = biggestVal;
    w = (m23-m32)*mult;
    y = (m12+m21)*mult;
    z = (m31+m12)*mult;
    break;
case :
    y = biggestVal;
    w = (m31 - m13) * mult;
    x = (m12 + m21) * mult;
    z = (m23 + m32) * mult;
    break;
case :
    z = biggestVal;
    w = (m12 - m21) * mult;
    x = (m31 + m13) * mult;
    y = (m23 + m32) * mult;
    break;
}

17、从欧拉角转换到四元数。

　　先将三个轴的旋转分别转换为四元数，再将这三个四元数连接成一个四元数。下面是分别旋转的四元数：

　　　　

　　将其连接起来即可得到结果。

　　　　

18、从四元转换到欧拉角

　　我们已经知道从四元数到矩阵，也知道从矩阵到欧拉角。下面是从矩阵求欧拉角：

　　

　　再下面是四元数求矩阵：

　　

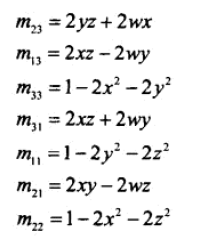
　　将图一中的 m 全部替换为 wxyz，即可得四元数到欧拉角的推导公式。

　　

// 使用全局变量保存输入输出
float w,x,y,z;
float h,p,b;

// 计算 si(pitch)
float sp = -2.0f * (y*z + w*x);

// 检查万向锁，允许有一定误差
if (fabs(sp)>0.9999f){
    // 向正上或正下看
    p = 1.570796f * sp;
    // 计算 heading, bank 置零
    h = atan2(-x*z - w*y, 0.5f - y*y - z*z);
    b = 0.0f;
}else{
    // 计算角度
    p = asin(sp);
    h = atan2(x*z - w*y, 0.5f - x*x - y*y);
    b = atan2(x*y - w*z, 0.5f - x*x, -z*z);
}

19、

20、