算法：非平衡二叉搜索树（UnBalanced Binary Search Tree）

背景

很多场景下都需要将元素存储到已排序的集合中。用数组来存储，搜索效率非常高： O(log n)，但是插入效率比较低：O(n)。用链表来存储，插入效率和搜索效率都比较低：O(n)。如何能提供插入和搜索效率呢？这就是二叉搜索树的由来，本文先介绍非平衡二叉搜索树。

非平衡二叉搜索树

规则

所有节点的左节点小于节点，所有节点的右节点大于等于自身，即：node.value >  node.left.value && node.value <= node.right.value。

示例

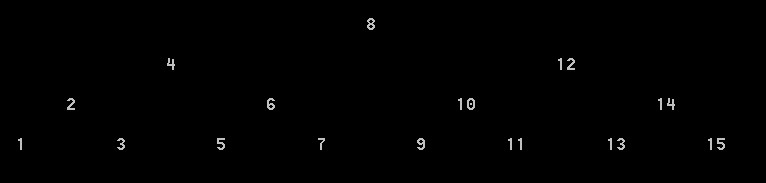
根据上面的规则，我们也很容易找到最大值和最小值，后面也会用到这种算法。最大值可以通过递归方法 node.right 得到，最小值可以递归 node.left 得到。

为什么叫非平衡？

说明：下图变成链表了，这会导致效率非常低，后面找机会再介绍平衡算法。

实现

搜索、遍历（前序、中序和后序）、添加算法都比较简单，可以直接看后面的代码，这里重点介绍一下删除算法。

如何删除元素？

第一步：要找到删除的元素（current）。

第二步：判断 current 满足如下哪种场景：

1. current.Right == null
   示例
   
   代码

                        if (parent == null)
                        {
                            this.Root = current.Left;
                        }
                        else if (isLeft)
                        {
                            parent.Left = current.Left;
                        }
                        else
                        {
                            parent.Right = current.Left;
                        }

   结果

   

2. current.Right != null && current.Right.Left == null
   示例
   
   代码

                        current.Right.Left = current.Left;
   
                        if (parent == null)
                        {
                            this.Root = current.Right;
                        }
                        else if (isLeft)
                        {
                            parent.Left = current.Right;
                        }
                        else
                        {
                            parent.Right = current.Right;
                        }

   结果

   

3. current.Right != null && current.Right.Left != null
   示例
   
   代码

                        Node<T> currentRightSmallestParent = current.Right;
                        var currentRightSmallest = current.Right.Left;
   
                        this.FindSmallest(ref currentRightSmallestParent, ref currentRightSmallest);
   
                        currentRightSmallestParent.Left = currentRightSmallest.Right;
                        currentRightSmallest.Left = current.Left;
                        currentRightSmallest.Right = current.Right;
                        if (parent == null)
                        {
                            this.Root = currentRightSmallest;
                        }
                        else if (isLeft)
                        {
                            parent.Left = currentRightSmallest;
                        }
                        else
                        {
                            parent.Right = currentRightSmallest;
                        }

   结果
   

   说明
   这里的重点是 FindSmallest，找出 current.Right.Left 子树中最小的元素，然后用它替换 current。

完整代码

 using System;
 using System.Collections.Generic;
 using System.Linq;
 using System.Text;
 using System.Threading.Tasks;

 namespace DataStuctureStudy.Trees
 {
     class UnBalancedBinarySearchTree
     {
         class Node<T>
             where T : IComparable<T>
         {
             public T Value { get; set; }

             public Node<T> Left { get; set; }

             public Node<T> Right { get; set; }

             public void InOrderTraverse(Action<T> action)
             {
                 if (this.Left != null)
                 {
                     this.Left.InOrderTraverse(action);
                 }

                 action(this.Value);

                 if (this.Right != null)
                 {
                     this.Right.InOrderTraverse(action);
                 }
             }

             public int Depth()
             {
                 var leftDepth = ;
                 var rightDepth = ;

                 if (this.Left != null)
                 {
                     leftDepth = this.Left.Depth();
                 }
                 if (this.Right != null)
                 {
                     rightDepth = this.Right.Depth();
                 }

                 return
                     leftDepth > rightDepth
                     ? leftDepth +
                     : rightDepth + ;
             }
         }

         public class Tree<T>
              where T : IComparable<T>
         {
             private Node<T> Root { get; set; }

             public void Display()
             {
                 Console.WriteLine();

                 if (this.Root == null)
                 {
                     return;
                 }

                 var depth = this.Root.Depth();
                 var buffers = new string[depth][];
                 for (int i = ; i < buffers.Length; i++)
                 {
                     buffers[i] = new string[(int)(Math.Pow(, depth) - )];
                 }

                 this.BuildArray(this.Root, depth, buffers, , );

                 for (int i = ; i < buffers.Length; i++)
                 {
                     for (int j = ; j < buffers[i].Length; j++)
                     {
                         if (buffers[i][j] == null)
                         {
                             Console.Write(new string(' ', ));
                         }
                         else
                         {
                             var leftPad = ( - buffers[i][j].Length) / ;
                             Console.Write(buffers[i][j]
                                 .PadLeft(leftPad + buffers[i][j].Length)
                                 .PadRight());
                         }
                     }
                     Console.WriteLine();
                     Console.WriteLine();
                 }
             }

             private void BuildArray(Node<T> node, int nodeDepth, string[][] buffers, int row, int startColumn)
             {
                 if (node == null)
                 {
                     return;
                 }

                 var nodeWidth = Math.Pow(, nodeDepth) - ;
                 var column = (int)(startColumn + nodeWidth / );

                 buffers[row][column] = node.Value.ToString();

                 this.BuildArray(node.Left, nodeDepth - , buffers, row + , startColumn);
                 this.BuildArray(node.Right, nodeDepth - , buffers, row + , column + );
             }

             public bool Contains(T item)
             {
                 var current = this.Root;

                 while (current != null)
                 {
                     if (item.CompareTo(current.Value) == )
                     {
                         return true;
                     }
                     else if (item.CompareTo(current.Value) < )
                     {
                         current = current.Left;
                     }
                     else
                     {
                         current = current.Right;
                     }
                 }

                 return false;
             }

             public void InOrderTraverse(Action<T> action)
             {
                 if (this.Root != null)
                 {
                     this.Root.InOrderTraverse(action);
                 }
             }

             public void Insert(T item)
             {
                 var node = new Node<T> { Value = item };

                 Node<T> parent = null;
                 var current = this.Root;
                 var isLeft = false;

                 while (current != null)
                 {
                     parent = current;

                     if (item.CompareTo(current.Value) < )
                     {
                         current = current.Left;
                         isLeft = true;
                     }
                     else
                     {
                         current = current.Right;
                         isLeft = false;
                     }
                 }

                 if (parent == null)
                 {
                     this.Root = node;
                 }
                 else if (isLeft)
                 {
                     parent.Left = node;
                 }
                 else
                 {
                     parent.Right = node;
                 }
             }

             public bool Delete(T item)
             {
                 Node<T> parent = null;
                 var current = this.Root;
                 var isLeft = false;

                 this.Find(item, ref parent, ref current, ref isLeft);

                 if (current == null)
                 {
                     return false;
                 }

                 if (current.Right == null)
                 {
                     if (parent == null)
                     {
                         this.Root = current.Left;
                     }
                     else if (isLeft)
                     {
                         parent.Left = current.Left;
                     }
                     else
                     {
                         parent.Right = current.Left;
                     }
                 }
                 else if (current.Right != null && current.Right.Left == null)
                 {
                     current.Right.Left = current.Left;

                     if (parent == null)
                     {
                         this.Root = current.Right;
                     }
                     else if (isLeft)
                     {
                         parent.Left = current.Right;
                     }
                     else
                     {
                         parent.Right = current.Right;
                     }
                 }
                 else
                 {
                     Node<T> currentRightSmallestParent = current.Right;
                     var currentRightSmallest = current.Right.Left;

                     this.FindSmallest(ref currentRightSmallestParent, ref currentRightSmallest);

                     currentRightSmallestParent.Left = currentRightSmallest.Right;
                     currentRightSmallest.Left = current.Left;
                     currentRightSmallest.Right = current.Right;
                     if (parent == null)
                     {
                         this.Root = currentRightSmallest;
                     }
                     else if (isLeft)
                     {
                         parent.Left = currentRightSmallest;
                     }
                     else
                     {
                         parent.Right = currentRightSmallest;
                     }
                 }

                 return true;
             }

             private void Find(T item, ref Node<T> parent, ref Node<T> current, ref bool isLeft)
             {
                 while (current != null)
                 {
                     if (item.CompareTo(current.Value) == )
                     {
                         break;
                     }

                     parent = current;

                     if (item.CompareTo(current.Value) < )
                     {
                         current = current.Left;
                         isLeft = true;
                     }
                     else
                     {
                         current = current.Right;
                         isLeft = false;
                     }
                 }
             }

             private void FindSmallest(ref Node<T> parent, ref Node<T> current)
             {
                 while (current != null)
                 {
                     if (current.Left == null)
                     {
                         break;
                     }

                     parent = current;
                     current = current.Left;
                 }
             }
         }
     }
 }

备注

学完这个树的最大收获就是，找到了一种输出树形结构相对高效的方法，比我之前用的高效，这种算法可以用在组织结构图的生成中。