【java排序】 归并排序算法、堆排序算法

一、归并排序算法

基本思想：

　　归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

归并排序示例：

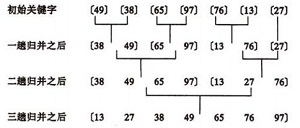
合并方法：

设r[i…n]由两个有序子表r[i…m]和r[m+1…n]组成，两个子表长度分别为n-i +1、n-m。

1. j=m+1；k=i；i=i; //置两个子表的起始下标及辅助数组的起始下标
2. 若i>m 或j>n，转⑷ //其中一个子表已合并完，比较选取结束
3. //选取r[i]和r[j]较小的存入辅助数组rf
   如果r[i]<r[j]，rf[k]=r[i]； i++； k++； 转⑵
   否则，rf[k]=r[j]； j++； k++； 转⑵
4. //将尚未处理完的子表中元素存入rf
   如果i<=m，将r[i…m]存入rf[k…n] //前一子表非空
   如果j<=n ,  将r[j…n] 存入rf[k…n] //后一子表非空
5. 合并结束。

算法实现：

　　/**
     * 归并排序
     * 简介:将两个（或两个以上）有序表合并成一个新的有序表 即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列
     * 时间复杂度为O(nlogn)
     * 稳定排序方式
     * @param nums 待排序数组
     * @return 输出有序数组
     */
    public static int[] sort(int[] nums, int low, int high) {
        int mid = (low + high) / 2;
        if (low < high) {
            // 左边
            sort(nums, low, mid);
            // 右边
            sort(nums, mid + 1, high);
            // 左右归并
            merge(nums, low, mid, high);
        }
        return nums;
    }

    /**
     * 将数组中low到high位置的数进行排序
     * @param nums 待排序数组
     * @param low 待排的开始位置
     * @param mid 待排中间位置
     * @param high 待排结束位置
     */
    public static void merge(int[] nums, int low, int mid, int high) {
        int[] temp = new int[high - low + 1];
        int i = low;// 左指针
        int j = mid + 1;// 右指针
        int k = 0;

        // 把较小的数先移到新数组中
        while (i <= mid && j <= high) {
            if (nums[i] < nums[j]) {
                temp[k++] = nums[i++];
            } else {
                temp[k++] = nums[j++];
            }
        }

        // 把左边剩余的数移入数组
        while (i <= mid) {
            temp[k++] = nums[i++];
        }

        // 把右边边剩余的数移入数组
        while (j <= high) {
            temp[k++] = nums[j++];
        }

        // 把新数组中的数覆盖nums数组
        for (int k2 = 0; k2 < temp.length; k2++) {
            nums[k2 + low] = temp[k2];
        }
    }

二、堆排序算法

1、基本思想：

　　堆排序是一种树形选择排序，是对直接选择排序的有效改进。

　　堆的定义下：具有n个元素的序列 （h1,h2,...,hn),当且仅当满足（hi>=h2i,hi>=2i+1）或（hi<=h2i,hi<=2i+1） (i=1,2,...,n/2)时称之为堆。在这里只讨论满足前者条件的堆。由堆的定义可以看出，堆顶元素（即第一个元素）必为最大项（大顶堆）。完全二 叉树可以很直观地表示堆的结构。堆顶为根，其它为左子树、右子树。

　　思想:初始时把要排序的数的序列看作是一棵顺序存储的二叉树，调整它们的存储序，使之成为一个 堆，这时堆的根节点的数最大。然后将根节点与堆的最后一个节点交换。然后对前面(n-1)个数重新调整使之成为堆。依此类推，直到只有两个节点的堆，并对 它们作交换，最后得到有n个节点的有序序列。从算法描述来看，堆排序需要两个过程，一是建立堆，二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函 数组成。一是建堆的渗透函数，二是反复调用渗透函数实现排序的函数。

2、实例

初始序列：46,79,56,38,40,84

　　建堆：

　　交换，从堆中踢出最大数

依次类推：最后堆中剩余的最后两个结点交换，踢出一个，排序完成。

3.算法实现：

 

public class HeapSort {
    public static void main(String[] args) {
        int[] a={49,38,65,97,76,13,27,49,78,34,12,64};
        int arrayLength=a.length;
        //循环建堆
        for(int i=0;i<arrayLength-1;i++){
            //建堆
            buildMaxHeap(a,arrayLength-1-i);
            //交换堆顶和最后一个元素
            swap(a,0,arrayLength-1-i);
            System.out.println(Arrays.toString(a));
        }
    }
    //对data数组从0到lastIndex建大顶堆
    public static void buildMaxHeap(int[] data, int lastIndex){
         //从lastIndex处节点（最后一个节点）的父节点开始
        for(int i=(lastIndex-1)/2;i>=0;i--){
            //k保存正在判断的节点
            int k=i;
            //如果当前k节点的子节点存在
            while(k*2+1<=lastIndex){
                //k节点的左子节点的索引
                int biggerIndex=2*k+1;
                //如果biggerIndex小于lastIndex，即biggerIndex+1代表的k节点的右子节点存在
                if(biggerIndex<lastIndex){
                    //若果右子节点的值较大
                    if(data[biggerIndex]<data[biggerIndex+1]){
                        //biggerIndex总是记录较大子节点的索引
                        biggerIndex++;
                    }
                }
                //如果k节点的值小于其较大的子节点的值
                if(data[k]<data[biggerIndex]){
                    //交换他们
                    swap(data,k,biggerIndex);
                    //将biggerIndex赋予k，开始while循环的下一次循环，重新保证k节点的值大于其左右子节点的值
                    k=biggerIndex;
                }else{
                    break;
                }
            }
        }
    }
    //交换
    private static void swap(int[] data, int i, int j) {
        int tmp=data[i];
        data[i]=data[j];
        data[j]=tmp;
    }
}